Zeichnen mit "wt...-Funktionen"
Hier soll die Benutzung der beiden wichtigsten 3D-Transformations-Funktionen vorgestellt werden, mit denen eine Translation bzw. eine Rotation des zu zeichnenden Objekts eingestellt wird. Mit t3translation(x,y,z) wird eine Translation eingestellt, die durch die Angabe von drei Komponenten in Richtung der 3D-Koordinaten bestimmt wird, mit t3rotation(phi,axis) wird eine Rotation um eine der drei Koordinatenachsen (welche das ist, wird durch den Parameter axis festgelegt) um den Winkel phi vorgegeben. Beide Funktionen arbeiten "additiv", fügen also zur gerade gültigen Transformation eine zusätzliche Verschiebung bzw. Drehung hinzu.
Beim Erzeugen eines CanvasGI-Objekts wird die 3D-Transformationsmatrix als Einheitsmatrix initialisiert, so dass zunächst die "wt...-Funktionen", die vor der Zeichenaktion die Transformation auf die zu zeichnenden Objekte anwenden, so arbeiten wie die "w...-Funktionen", die die Transformationsmatrix unberücksichtigt lassen.
Die nebenstehend zu sehende Zeichenfläche wurde mit einer vereinfachten Version des Beispiel-Programms "Projektion 2" erzeugt. Das Bild beim Start dieser Seite ist identisch mit dem Bild, das auf der Seite Projektionen, Beispielprogramm "Projektion 1" erzeugt wird. Die in der Funktion draw realisierten Zeichenaktionen unterscheiden sich nur minimal von den Funktionsaufrufen des Programms "Projektion 1". Hier werden "wt...-Funktionen" verwendet:
function draw () {
gi.clearcanvas ("silver" , "black") ; // ... fuellt Canvas-Bereich mit Hintergrundfarbe
// ("silver") und zeichnet schwarzen Rahmen
gi.wtdrawline (-5000 , 0 , 0 , 10000 , 0 , 0 , "black") ;
gi.wtdrawline ( 0 , -5000 , 0 , 0 , 10000 , 0 , "red") ;
gi.wtdrawline ( 0 , 0 , -5000 , 0 , 0 , 10000 , "blue") ;
var xcoor = new Array (5000 , 0 , 0) ;
var ycoor = new Array ( 0 , 8000 , 0) ;
var zcoor = new Array ( 0 , 0 , 4000) ;
gi.wtdrawfpolygon (xcoor , ycoor , zcoor , "yellow" , "maroon") ;
}
- Alle CanvasGI-Funktionen, deren Namen mit "wt..." beginnen, erwarten "World coordinates" (Koordinatentripel, die sich auf ein kartesiches 3D-Koordinatensystem beziehen). Diese werden vor der Zeichenaktion der jeweils gültigen Transformation unterworfen. Die Funktionen, deren Namen mit "wtdraw..." beginnen, zeichnen direkt (sammeln die Ausgabe nicht erst in einem "Path").
- Die Funktion wtdrawline erwartet die Koordinaten zweier Punkte P1 und P2 in der Reihefolge x1, y1, z1, x2, y2, z2 und verbindet diese Punkte mit einer geraden Linie mit einer (optional vorzugebenen) Farbe.
- Die Funktion wtdrawfpolygon erwartet drei Arrays mit den x-Koordinaten, den y-Koordinaten und den z-Koordinaten der durch ein geschlossenes Polygon zu verbindenden Punkte. Die Länge des x-Koordinaten-Arrays bestimmt die Anzahl der Eckpunkte. Optional können zusätzlich die "Fillcolor" und die "Strokecolor" vorgegeben werden.
Änderung der Transformation
Über die Buttons unterhalb der Zeichenfläche werden Änderungen der Transformationsmatrix ausgelöst. Dies ist zum Beispiel für die Translationen folgendermaßen programmiert:
<input type="button" value="x+" name="plusx"
style="width:34px; height:27px; font-size:small;" onclick="xplus (1000,0,0);" />
<input type="button" value="y+" name="plusx"
style="width:34px; height:27px; font-size:small;" onclick="xplus (0,1000,0);" />
<input type="button" value="z+" name="plusx"
style="width:34px; height:27px; font-size:small;" onclick="xplus (0,0,1000);" />
<input type="button" value="x-" name="plusx"
style="width:34px; height:27px; font-size:small;" onclick="xplus (-1000,0,0);" />
<input type="button" value="y-" name="plusx"
style="width:34px; height:27px; font-size:small;" onclick="xplus (0,-1000,0);" />
<input type="button" value="z-" name="plusx"
style="width:34px; height:27px; font-size:small;" onclick="xplus (0,0,-1000);" />
function xplus (x , y , z) {
gi.t3translation (x , y , z) ;
draw () ;
}
|
Beim Anklicken eines Buttons der oberen Reihe wird also immer eine Funktion xplus aufgerufen, der die drei Komponenten der Translation übergeben werden. Die Funktion ist nebenstehend zu sehen. Mit gi.t3translation(x,y,z) wird die entsprechende Translation zur vorab gültigen Transformation hinzugefügt. Hier ist es jeweils eine Verschiebung parallel zu einer Koordinatenachse der "World coordinates" um 1000 Einheiten.
Entsprechend sind die Aktionen für die Rotationen programmiert:
<input type="button" value="φx+" name="plusx"
style="width:34px; height:27px; font-size:small;" onclick="phiplus (Math.PI/18,gi.AXIS_X);" />
<input type="button" value="φy+" name="plusx"
style="width:34px; height:27px; font-size:small;" onclick="phiplus (Math.PI/18,gi.AXIS_Y);" />
<input type="button" value="φz+" name="plusx"
style="width:34px; height:27px; font-size:small;" onclick="phiplus (Math.PI/18,gi.AXIS_Z);" />
<input type="button" value="φx-" name="plusx"
style="width:34px; height:27px; font-size:small;" onclick="phiplus (-Math.PI/18,gi.AXIS_X);" />
<input type="button" value="φy-" name="plusx"
style="width:34px; height:27px; font-size:small;" onclick="phiplus (-Math.PI/18,gi.AXIS_Y);" />
<input type="button" value="φz-" name="plusx"
style="width:34px; height:27px; font-size:small;" onclick="phiplus (-Math.PI/18,gi.AXIS_Z);" />
function phiplus (phi , axis) {
gi.t3rotation (phi , axis) ;
draw () ;
}
|
Beim Anklicken eines Buttons der unteren Reihe wird also immer eine Funktion phiplus aufgerufen, der der Winkel und die Rotationsachse der Rotation übergeben werden. Die Funktion ist nebenstehend zu sehen. Mit gi.t3rotation(phi,axis) wird die entsprechende Rotation zur vorab gültigen Transformation hinzugefügt. Hier ist es jeweils eine Drehung um 10° (anzugeben im Bogenmaß: π/18) um eine der drei Koordinatenachsen, für die die CanvasGI-Variablen gi.AXIS_X, gi.AXIS_Y bzw. gi.AXIS_Z verwendet werden.
Beim Anklicken des Buttons "Reset" wird die Funktion ResetTrans aufgerufen:
<input type="button" value="Reset" name="Reset"
style="width:55px; height:64px; font-size:small;" onclick="ResetTrans ();" />
function ResetTrans () {
gi.tinit () ;
draw () ;
}
|
Die Funktion ResetTrans ist nebenstehend zu sehen. Mit gi.tinit() wird die Transformationsmatrix wieder zur Einheitsmatrix, so dass alle folgenden Zeichenaktionen mit den Originalkoordinaten ausgeführt werden.
Das Beispiel-Programm "Projektion 2" enthält alle hier beschriebenen Bausteine und gestattet darüber hinaus die Änderung der Projektion.
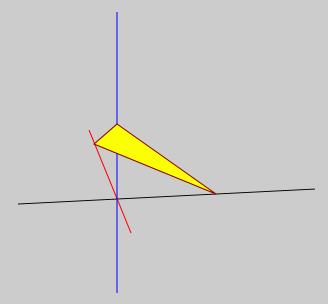
Hinweis zur Darstellung der Zeichenfläche rechts oben auf dieser Seite und zum Programm "Projektion 2":
Wenn man die Darstellung rotieren lässt, ist sie in bestimmten Lagen fehlerhaft. Das nebenstehend zu sehende Bild entsteht zum Beispiel, wenn man dreimal auf den Button "φz+" klickt. Es sieht so aus, als läge das gelbe Dreieck vor der blauen Linie, was falsch ist und daran liegt, dass die blaue Linie vor dem Dreieck gezeichnet wird.
Solche Bilder korrekt darzustellen, ist ein gesondert zu behandelndes (nicht ganz einfaches) Problem und wird auf der Seite 3D-Probleme: "Hidden lines", "Edges", "Silhouette lines", "Lightness" behandelt und anschließend an mehreren Beispielen demonstriert.
Weiterlesen
Auf der folgenden Seite wird gezeigt, wie man 3D-Modelle beschreiben und mit den hier beschriebenen Transformationen und Projektionen darstellen kann:
- Empfehlung zum Weiterlesen: "Einfache 3D-Modelle".
Folgende Seiten werden als Einführung in die Benutzung der 3D-Grafik mit CanvasGI empfohlen:

