|
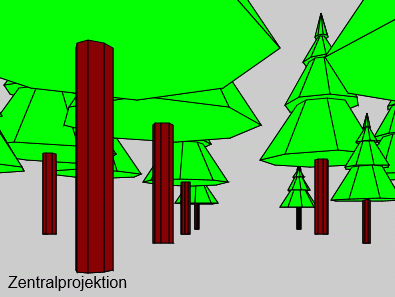
| Nur mit Zentralprojektion möglich: Man steht im Wald |
Das Problem
Während die Darstellungen mit der Parallelprojektion bei beliebigen Parametern weitgehend unkritisch (und deshalb in der Regel zu bevorzugen) sind, bietet die Zentralprojektion zusätzliche Möglichkeiten und damit auch Risiken (man beachte die Bemerkungen zum Versagen der Projektionsformeln am Ende der theoretischen Darstellung auf der Seite "Mathematik der Zentralprojektion").
Wenn der "Eye point" in ausreichender Entfernung von dem darzustellenden Objekt liegt, gibt es bei der Zentralprojektion eigentlich keine Probleme. Die Möglichkeit, den "Eye point" auch in das darzustellende Objekt hineinzulegen (vgl. nebenstehende Abbildung), verlangt einige besondere Maßnahmen, die der Programmierer zu beachten hat. Hier werden die Probleme diskutiert und die Vorsichtsmaßnahmen beschrieben, die in den CanvasGI-Funktionen eingebaut sind, um einerseits kritische Operationen zu vermeiden, andererseits möglichst mit jeder Einstellung "ein vernünftiges Bild" zu erzeugen. Hier werden zunächst die zu beachtenden Probleme gelistet:
- Prinzipiell sind nur Punkte darzustellen, die im "Blickfeld" des Betrachters liegen. Eine natürliche Grenze ist durch eine Ebene gegeben, die durch den "Eye point" geht und parallel zur Projektionsebene liegt. Diese Ebene ("Vanishing plane") teilt den Raum in zwei Halbräume auf. Punkte, die in dem Halbraum liegen, in dem sich die Projektionsebene nicht befindet ("Forbidden half space") werden nicht dargestellt. Aber natürlich können auch Punkte, die in der "Vanishing plane" liegen, nicht dargestellt werden, weil der Sehstrahl parallel zur Projektionsebene liegt. Deshalb muss dafür gesorgt werden, dass nur Punkte jenseits einer zwischen Projektionsebene und "Vanishing plane" liegenden (und zu beiden parallelen) Ebene dargestellt werden. Letztere darf durchaus sehr nah an der "Vanishing plane" liegen und wird in der englischsprachigen Literatur als "Near clipping plane" oder "Hither clipping plane" bezeichnet.
- Weder der Mensch noch eine Kamera haben gleichzeitig alle Punkte des "erlaubten Halbraumes" im Blick. Deshalb sollten für einen realitätsnahen Eindruck nur Punkte aus einem Kegel berücksichtigt werden, dessen Spitze mit dem "Eye point" zusammenfällt und dessen Höhe die Projektionsebene senkrecht schneidet. Der Öffnungswinkel des Kegels ("Kamera-Winkel", "Field-of-vision-angle") bestimmt das Blickfeld. Dieser Kegel schneidet einen Kreis aus der Projektionsebene heraus. Da aber üblicherweise keine kreisförmigen Bilder angefertigt werden, wird ein Quadrat gewählt, dessen Seitenlängen dem Durchmesser des Kreises entsprechen. An die Stelle des beschriebenen Kegels tritt also eine vierseitige (quadratische) Pyramide (mit unendlicher Höhe).
- Vielfach ist es sinnvoll, auch sehr weit vom Betrachter entfernte Punkte nicht mehr darzustellen. Dann definiert man noch eine (ebenfalls zur Projektionsebene parallel liegende) "Far clipping plane" ("Yon clipping plane"). Wenn nur Punkte abgebildet werden, die innerhalb der vierseitigen Pyramide und zwischen den beiden "Clipping planes" liegen, so ist der Raum, in dem diese Punkte liegen, ein quadratischer Pyramidenstumpf ("Viewing frustum").
- Der Test, ob ein Punkt innerhalb des "Viewing frustums" liegt, kann recht aufwendig sein. Der Aufwand wird noch dadurch erheblich vergrößert, dass Linien (es genügt, wenn man sich das nur für gerade Linien verdeutlicht), deren Endpunkte außerhalb des "Viewing frustums" liegen, durchaus zum Teil innerhalb liegen können, so dass Schnittpunkte berechnet werden müssten.
Realisierung in CanvasGI
In CanvasGI sind einige Vorsichtsmaßnahmen getroffen worden, die (bei recht geringem Aufwand) die meisten der genannten Probleme umgehen, so dass der Programmierer in der Regel auf die (für ihn und das Programm) aufwendigen Algorithmen zur Realisierung der beschriebenen "3D-Clipping-Strategie" verzichten kann. Mit dem nebenstehend zu sehenden Bild, einer Modifikation des auf der Seite "Modell mehrfach kopieren, Zoom and Move" ausführlich erläuterten "Waldes", kann man die folgenden Eigenschaften der CanvasGI-Funktionen erproben:
- Zur Klasse CanvasGI gehört der "Kamera-Winkel" als Wert im Bogenmaß. Er kann mit prgetangleofview abgefragt werden und mit prsetangleofview auf einen anderen Wert gesetzt werden. Er wird mit π/4 vorbelegt. Dieser Wert (45°) ist für die meisten Darstellungen ausreichend, man bedenke, dass eine normale Kamera mit einem gängigen Objektiv einen "Kamera-Winkel" von weniger als 40° hat (man beachte, dass in dem Bild mit den Startwerten eine Verkleinerung des Kamera-Winkels wenig ändert, weil der "Eye point" so weit vom Objekt entfernt ist, dass man dieses auch bei kleinem Winkel komplett sieht).
- Der "Kamera-Winkel" wird nur in der Funktion
ptlimits benutzt. Mit dieser Funktion
werden die Maxima und Minima der 2D-"User coordinates" berechnet, die sich aus
allen 3D-"World coordinates"-Punkten ergeben, wenn auf diese die aktuelle
Transformation und die eingestellte Projektion angewendet werden.
Zwei Einschränkungen werden zusätzlich gemacht:
- Punkte des "Forbidden Halfspace" werden überhaupt nicht berücksichtigt, ebensowenig Punkte, deren Abstand vom "Eye point" kleiner als 1/1000 der Strecke auf dem Sehstrahl vom "Eye point" bis zur Projektionsebene ist (die also "fast im Auge liegen").
- Nachdem die Minima und Maxima aller Punkte in der Projektionsebene berechnet wurden, wird das so ermittelte Rechteck gegebenenfalls noch verkleinert auf die Abmessungen, die der "Kamera-Winkel" vorgibt, so dass die von ptlimits zurückgegebenen Werte nicht den Bereich des Quadrats überschreiten, den das "Viewing frustum" aus der Projektionsebene herausschneidet.
- Die "zeichnenden" CanvasGI-3D-Funktionen zeichnen nicht, wenn eine der ihnen übergebenen Koordinaten im "Forbidden halfspace" oder so nah wie oben beschrieben am "Eye point" liegt.
Das "Clipping" wird also in den 2D-Bereich verlegt (und ist damit nicht sonderlich aufwendig). Linien, deren Endpunkte außerhalb des "Viewing frustums" liegen, sind also mit einem eventuell sichtbaren Anteil durchaus zu sehen. Es fehlen nur die Linien, bei denen ein Punkt im "Forbidden halfspace" (oder "beinahe im Auge") liegt und die trotzdem einen Teil innerhalb des "Viewing frustums" haben. Diese seltenen Ausnahmen rechtfertigen aber kaum eine aufwendige Schnittpunktberechnung.

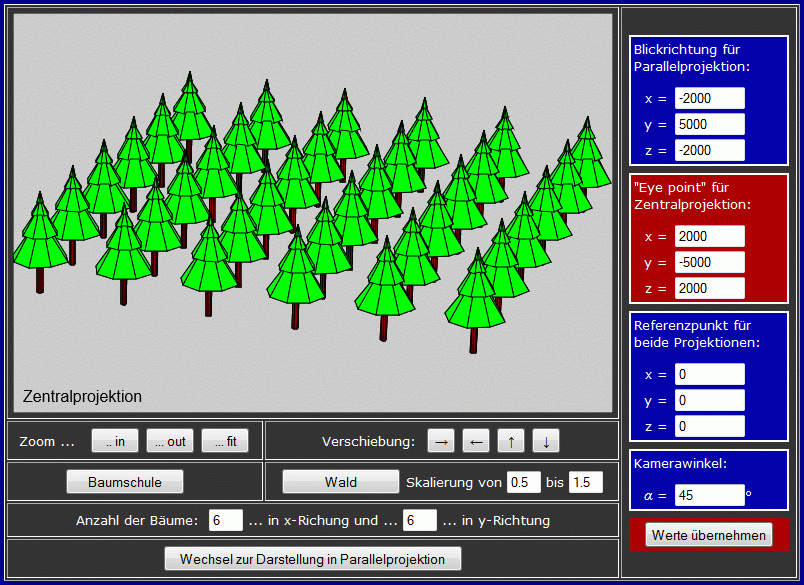
Man kann das alles ausprobieren mit dem "Canvas", der hier einen "Wald" zeigt mit den Angeboten zur Einstellung der Projektionsparameter einschließlich Kamera-Winkel. Dazu sollte man ungefähr wissen, was mit welchen Abmessungen dargestellt wird (bei der Zentralprojektion kann es durchaus passieren, dass man "ins Leere" blickt):
Die 36 "Bäume" stehen in einem Quadrat auf der x-y-Ebene, der Fußpunkt des Stammes des Baumes vorn links hat die Koordinaten (0,0,0), der Fußpunkt des Stammes des Baumes hinten rechts hat die Koordinaten (75,75,0). Man darf sich die Dimension "Meter" dazudenken. Die x-Achse verläuft also entlang der vorderen Baumreihe, die y-Achse entlang der linken Baumreihe.
Dann steht also ein Betrachter mit dem "Eye point" - wie nebenstehend angegeben - im Wald ("Eye point" entspricht etwa der Augenhöhe) und blickt geradeaus "von (35,20,1.6) nach (35,100,1.6)". Diese Parameter werden automatisch eingestellt, wenn man oben auf das Menüangebot "So sieht es ein Spaziergänger im Wald" klickt.
Auch den Einfluss des Kamera-Winkels sollte man ausprobieren. Allgemein mag folgende Empfehlung gelten: Wenn der "Eye point" innerhalb des Objekts liegt, liefern kleinere Kamera-Winkel schönere Ansichten, bei "Außen-Ansichten" sollte man den voreingestellten Winkel (45°) akzeptieren, eventuell auch einen größeren Winkel wählen, was allerdings sehr schnell zu deutlichen Verzerrungen an den Bildrändern führt.
Beipiel-Programm "Spezielle Probleme der Zentralprojektion, Kamera-Winkel"
Das Beipiel-Programm "Spezielle Probleme der Zentralprojektion, Kamera-Winkel" enthält neben den oben beschriebenen Funktionen noch weitere Angebote. Es startet mit folgendem Bild:
- Man kann also die Anzahl der Bäume beliebig einstellen und auch für den Vergleich zur Darstellung in Parallelprojektion wechseln.
Weiterlesen
- Empfehlung zum Weiterlesen: Auf der Seite "3D-Flächen" wird die Darstellung von Flächen im Raum behandelt, die durch mathematische Funktionen beschreibbar sind.