CanvasGI: 2D-Transformationen

Strategie für die Animation

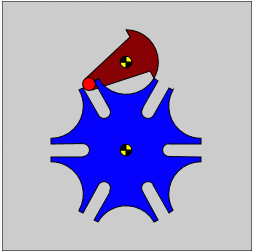
Am Beispiel des Malteserkreuzes, dessen Konstruktion auf der Seite "Anwendung ebener Transformationen" ausführlich beschrieben wird (rechts sieht man das Ergebnis), soll gezeigt werden, wie es gelingt, Bewegung in das Bild zu bringen:

• Prinzipiell ist dies recht einfach, wie nachfolgend für die Kurbel gezeigt wird.
• Schwierig wird es nur dadurch, dass wie in diesem Fall der mathematische Zusammenhang zwischen der Bewegung der Kurbel und der Bewegung des Malteserkreuzes gefunden und als Animation realisiert werden muss.

Die prinzipielle Strategie für eine Animation kann wie folgt beschrieben werden:

• Zeichnen des Systems in einer bestimmten Lage,
• Einstellen einer neuen Transformation, Löschen des vorherigen Bildes und Zeichnen unter Verwendung der neuen Transformation, und diese Aktion ständig wiederholen.

Die Kurbel dreht sich

Die Lage der Kurbel wird in der Funktion crank bei der Konstruktion des Malteserkreuzes durch eine Rotations-Transformation bestimmt, die mit dem Rotationswinkel phi0 festgelegt wird:

gi.trot (0 , L , phi0) ;

Die CanvasGI-Funktion trot arbeitet inkrementell, so dass bei jedem Aufruf eine zusätzliche Rotation hinzukommt. Es würde sich also anbieten, diese Funktion ständig mit einem DeltaPhi aufzurufen. Diese einfache Variante scheidet hier aus, weil verschiedene Rotationen (Kurbel und Malteserkreuz) zu verwalten sind. Deshalb wird folgende (besonders einfache) Strategie gewählt: Der Winkel phi0 für den Aufruf von trot wird jeweils um DeltaPhi erhöht, und vor jedem trot-Aufruf wird die gesamte Transform mit tinit "auf Null gestellt".

Deshalb wird der Winkel phi0 als Variable betrachtet, die nach jeweils einer bestimmten Zeit DeltaT um den Winkel DeltaPhi verändert wird. Der Bereich, in dem die globalen Variablen vereinbart sind, wird also zum Beispiel um diese beiden (hellblauen) Zeilen ergänzt

      var phi0 = -Math.PI/3 ;
      
      var DeltaT   = 50 ;
      var DeltaPhi = Math.PI/20 ;

In der Funktion init, die beim Start der Seite aufgerufen wird, und in der aus ihr gestarteten Funktion draw sind folgende minimalen Änderungen vorzunehmen (hellblaue Zeilen):

      function draw () {
         gi.clearcanvas    ("silver" , "black") ;  // ... fuellt Canvas-Bereich mit Hintergrundfarbe
                                                   //     ("silver") und zeichnet schwarzen Rahmen
         crank  () ;                               // ... zeichnet die Kurbel
         cross  () ;                               // ... zeichnet das Malteserkreuz
         pivots () ;                               // ... zeichnet die Lager
         phi0 += DeltaPhi ;
      }

      function init () {
         gi = new canvasGI ("canvas") ;            // Ein "CanvasGI-Objekt" wird erzeugt
         gi.setusercoordsi (-L , -L , L , L+R+Rs , 5) ;
         window.setInterval ("draw ()" , DeltaT) ;
      }

• Mit dem Aufruf von window.setInterval wird erreicht, dass die als erster Parameter übergebene Funktion draw kontinuierlich in einem festgelegten Rhythmus aufgerufen wird. Der zweite Parameter gibt die Länge der Pause zwischen zwei Aufrufen vor (Maßeinheit: Millisekunden).
• Die über window.setInterval ständig aufgerufene Funktion draw löscht zunächst das alte Bild, zeichnet ein neues und erhöht den Winkel für die Transformation der Kurbel. Rechts sieht man den Effekt: Die Kurbel dreht sich.
• Man beachte, dass die für die (statische) Zeichnung der Kurbel auf der Seite Konstruktion des Malteserkreuzes erzeugte Funktion crank ungeändert übernommen werden konnte. Lediglich der für die Rotations-Transformation in der Funktion verwendete Winkel phi0 wird nun (von außen) kontinuierlich geändert.

Synchronisation der Bewegungen von Kurbel und Kreuz

Zwei Probleme sind zu lösen, um dem Kreuz die zur Kurbelbewegung passende Drehbewegung aufzuzwingen:

• Das Kreuz darf sich nur bewegen, wenn der Mitnehmer der Kurbel im Eingriff ist. Weil für den Winkel phi0 die untere tiefste Lage als phi0 = 0 gewählt wurde (deshalb Startstellung phi0 = −π/3), darf die Rotation des Kreuzes nur erfolgen, wenn −π/3 ≤ phi0 ≤ π/3 gilt. Das kann durch eine Abfrage im Programm leicht realisiert werden.
• Der mathematische Zusammenhang zwischen dem Kurbelwinkel phi0 und dem Winkel, um den sich das Kreuz dreht, ist mit einigen geometrischen Überlegungen zu finden. Ausführlich wird dieses Getriebe im Kapitel "Kinematik starrer Körper" des Lehrbuchs "Dankert/Dankert: Technische Mechanik" beschrieben. Wenn mit ψ (im Programm: psi) der Winkel bezeichnet wird, um den sich das Kreuz bei Kurbeleingriff dreht (das Kreuz also einer Rotations-Transformation um diesen Winkel unterworfen werden muss), kann die dort hergeleitete Formel in folgender Form verwendet werden:

  

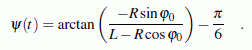
Die Funktion cross wird also um die folgenden (hellblauen) Zeilen ergänzt, die genau diese beiden Bedingungen realisieren:

       function cross () {
         gi.tinit     () ;
         if (phi0 > -Math.PI/3 && phi0 < Math.PI/3) {                     // Kurbel im Eingriff
             var psi = Math.atan ((-R * Math.sin(phi0))/(L - R * Math.cos(phi0))) - Math.PI/6 ;
             gi.trot (0 , 0 , psi) ;
         }
         gi.beginpath () ;
         ...

Weil der Winkel phi0 unbegrenzt wächst, würde die oben programmierte Abfrage nur bei der ersten Kurbelumdrehung funktionieren. Dieser Mangel wird geheilt durch das Rücksetzen des Winkels nach Erreichen einer vollen Umdrehung. Dies wird in der Funktion draw ergänzt (hellblaue Zeile):

      function draw () {
         gi.clearcanvas    ("silver" , "black") ;  // ... fuellt Canvas-Bereich mit Hintergrundfarbe
                                                   //     ("silver") und zeichnet schwarzen Rahmen
         crank  () ;                               // ... zeichnet die Kurbel
         cross  () ;                               // ... zeichnet das Malteserkreuz
         pivots () ;                               // ... zeichnet die Lager
         phi0 += DeltaPhi ;
         if (phi0 > 3*Math.PI/2) { phi0 -= 2*Math.PI ; }
      }

Das hier entwickelte Programm kann als c_malteseranimation.html, in einem separaten Fenster gestartet werden. Hier findet man eine etwas erweiterte Version, die das Stoppen und Starten der Bewegung und die Änderung der Geschwindigkeit gestattet.

Weiterlesen

Empfehlung zum Weiterlesen:" Canvas3D: Projektion auf eine ebene Zeichenfläche".

Folgende Seiten werden als Einführung in die Benutzung des CanvasGI empfohlen:

• "Benutzer-Koordinaten (User coordinates)", isotrope und anisotrope Skalierung,
• "Ebene Transformationen",
• "Anwendung ebener Transformationen: Konstruktion eines Malteserkreuzes".