Kartesische Koordinaten
Es wird die so genannte geometrische Transformation betrachtet, bei der ein Objekt in einem festen Koordinatensystem bewegt wird.
Es genügt, das "Schicksal" eines Punktes bei einer Transformation zu untersuchen. In allen Fällen wird im folgenden die "alte" Lage des Punktes durch die Koordinaten x und y beschrieben, die Lage nach der Transformation durch die Koordinaten x' und y'.
Es werden folgende vier sehr einfache Transformationen beschrieben (Translation, Rotation um den Nullpunkt, Skalierung bezüglich des Nullpunktes, Spiegelung an den Koordinatenachsen), aus denen sich durch geeignete Verknüpfungen beliebige andere Transformationen zusammensetzen lassen:
- Bei einer Translation bewegen sich alle Punkte des Objekts auf
kongruenten Bahnen. Die Koordinaten aller Punkte mögen die Veränderungen
tx und ty
erfahren, so daß die neue Lage eines Punktes durch
beschrieben wird.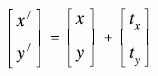
- Bei einer Rotation dreht sich das Objekt um einen bestimmten Winkel um eine
vorzugebende Achse, beim ebenen Problem also um einen vorzugebenden Punkt.
Mit einer kleinen Skizze macht man sich leicht klar, daß bei einer Rotation eines
Punktes um den Nullpunkt um den (entgegen dem Uhrzeigersinn positiv gezählten)
Winkel φ folgende Transformation gilt:
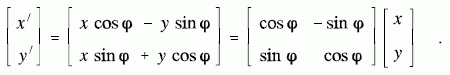
- Bei der Skalierung werden die Abmessungen des Objekts vergrößert
(Skalierungsfaktoren größer als 1) bzw. verkleinert. Die Skalierung bezieht
sich immer auf einen zu definierenden Punkt, der dann selbst seine Lage nicht
verändert, während alle anderen Punkte ihren Abstand vom Bezugspunkt
vergrößern oder verkleinern. Bei der Skalierung bezüglich des Nullpunktes
mit den Skalierungsfaktoren sx
und sy (jeweils in Richtung der
Koordinatenachsen) berechnet sich die Lage des neuen Punktes nach
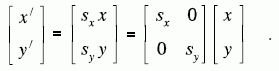
- Bei einer Spiegelung eines Objektes an der y-Achse
ändern alle x-Koordinaten
der Punkte ihr Vorzeichen:
Dementsprechend gilt für die Spiegelung eines Objektes an der x-Achse: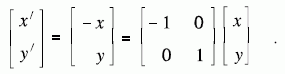
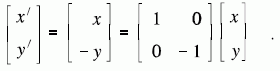
Da sich die Translation als einzige Transformation in kartesischen Koordinaten nicht durch eine Transformationsmatrix beschreiben läßt, kann hier erstmals mit Vorteil von den homogenen Koordinaten Gebrauch gemacht werden. Die kartesischen Koordinaten werden um λ = 1 ergänzt, und alle Transformationen lassen sich einheitlich durch Transformationsmatrizen beschreiben. Während für die Translation das Aufschreiben der Beziehung als Multiplikation "Matrix * Vektor" überhaupt erst möglich wird, werden die Transformationsmatrizen für die Rotation, die Skalierung und die Spiegelung um eine einfache Zeile bzw. Spalte ergänzt ("gerändert"). Diese Formeln werden nachfolgend zusammengestellt.
Ebene geometrische Transformation mit homogenen Koordinaten
Die nachfolgend angegebenen Formeln sind im CanvasGI für die ebenen Transformationen realisiert:

Verknüpfung von Transformationen
Aus den oben angegebenen Elementartransformationen können beliebige Transformationen durch das Ausführen von mehreren Transformationen nacheinander realisiert werden. Dabei ist zu beachten, dass eine Transformation immer durch Linksmultiplikation mit der entsprechenden Transformationsmatrix realisiert wird, so dass schließlich ein Produkt mehrerer Transformationsmatrizen die Gesamt-Transformation beschreibt, bei der die Matrix der letzten Transformation links steht.
Dies soll an einem einfachen Beispiel gezeigt werden: Es ist die geometrische Transformationsmatrix zu bestimmen, mit der die Rotation eines Punktes (x,y) um einen Winkel φ (im Uhrzeigersinn) um den beliebigen Drehpunkt (xM,yM) erzeugt wird. Da in den Elementartransformationen nur der Fall "Rotation um den Nullpunkt" vorgesehen ist, wird folgendermaßen vorgegangen:
Zunächst wird der der Punkt (xM,yM) in den Nullpunkt verschoben ("Translation 1" mit tx = −xM und ty = −yM), danach kann die Rotation um den Nullpunkt ausgeführt werden, schließlich muss die Verschiebung rückgängig gemacht werden ("Translation 2" mit tx = xM und ty = yM ). Folgende Matrizen sind also zu multiplizieren:
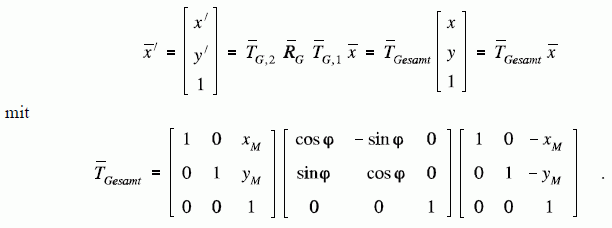
Man beachte, dass eine Vertauschung der Reihenfolge zweier Transformationen in der Regel auf eine ganz andere Gesamt-Transformation führt. In der mathematischen Beschreibung verknüpfter Transformationen mit homogenen Koordinaten wird dies durch die Matrizen-Produkte der Transformationsmatrizen deutlich: Im Gegensatz zum Produkt skalarer Größen ist das Matrix-Produkt nicht kommutativ.
Das CanvasGI enthält stets eine Transformationsmatrix für die ebene Transformation und eine Transformationsmatrix für die 3D-Transformation. Beide Matrizen werden als Einheitsmatrizen initialisiert, so dass zunächst keine Unterschiede bei der Verwendung der zeichnenden Funktionen, die die Transformation auswerten, und den "gewöhnlichen" Zeichenfunktionen bestehen. Erst dann, wenn mit den entsprechenden Funktionen eine Transformation geändert wurde, macht sich dies (nur) bei den speziellen Zeichenfunktionen bemerkbar. Die Namen der Zeichenfunktionen, die die ebene Transformation auswerten, beginnen alle mit ut bzw. utdraw.
Weiterlesen
Folgende Seiten werden als Einführung in die Thematik "Transformationen" empfohlen:
- Empfehlung zum Weiterlesen:" Anwendung ebener Transformationen: Konstruktion eines Malteserkreuzes",
- "Transformationen, homogene Koordinaten".

