Koordinatensysteme
Als Ergänzung zu den mit Gerätekoordinaten (Pixel) arbeitenden "Viewport coordinates" (vorgestellt auf der Seite "Viewports und Clipping") werden hier problembezogene Koordinaten definiert, als
Benutzer-Koordinaten ("User coordinates"):
Für den "Current viewport" wird ein Koordinatensystem durch Angabe der Koordinaten zweier Punkte P1 und P2 definiert. P1 ist stets die LINKE UNTERE, P2 die RECHTE OBERE Ecke eines rechteckigen Zeichenbereichs. Zunächst darf angenommen werden, daß diese beiden Punkte mit den entsprechenden Ecken des "Current viewport" identisch sind (tatsächlich gilt dies nur für "anisotrope Skalierung ohne Rand").
- Für das Zeichnen unter Verwendung der "User coordinates" gibt es spezielle Funktionen, deren Namen mit u (definieren eine Aktion für einen Pfad) bzw. udraw (zeichnen sofort) beginnen.
- Für P1 und P2 dürfen beliebige Werte festgelegt werden. Der Ursprung des Koordinatensystems kann dabei durchaus außerhalb des "Current viewport" liegen. Da die Koordinatenachsen natürlich immer so gerichtet sind, dass sie von kleineren zu größeren Werten zeigen, können mit den Koordinaten der Definitions-Punkte P1 und P2 alle vier Kombinationen realisiert werden (wenn die beiden P1-Koordinaten kleiner sind als die entsprechenden P2-Koordinaten, zeigt die x-Achse nach rechts, und die y-Achse ist nach oben gerichtet).
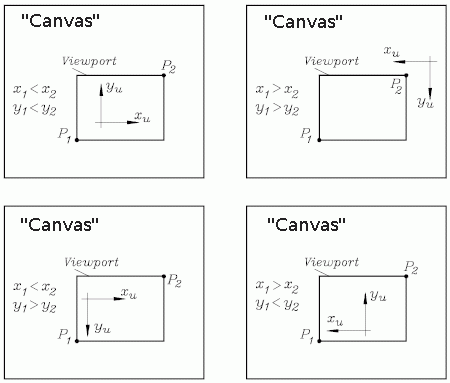
Die nebenstehende Abbildung zeigt die vier Möglichkeiten, die sich für die Richtungen der Achsen der "User coordinates" ergeben können. Alle nachfolgenden Aufrufe von "u...-Routinen" bzw. "udraw...-Routinen" beziehen sich dann auf diese Koordinatensysteme.
Das oben rechts dargestellte Beispiel zeigt ein Koordinatensystem, dessen Ursprung (in diesem Fall durch Angabe ausschließlich positiver Koordinaten für P1 und P2) außerhalb des "Current viewport" liegt.
Zur Definition der "User coordinates" stehen zwei Funktionen zur Verfügung:
- setusercoordsa skaliert "anisotrop" (unterschiedlich in den beiden Richtungen), so dass die Viewport-Fläche optimal genutzt wird (sinnvoll z. B. für die Darstellung von Diagrammen, wenn die beiden Koordinaten Größen unterschiedlicher Dimensionen repräsentieren).
- setusercoordsi skaliert "isotrop" (gleichmäßig in den beiden Richtungen), so dass die Viewport-Fläche in der Regel nur in einer Richtung optimal genutzt wird (sinnvoll z. B. für die Darstellung von Bahnkurven, damit diese nicht verzerrt werden).
Beiden Funktionen kann optional ein Parameter übergeben werden, der einen Rand erzwingt.
Beispiel-Programm (anisotrope Skalierung)
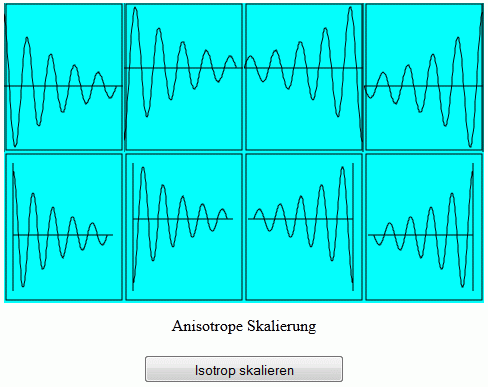
Im nachfolgend beschriebenen Beispiel-Programm wird in jeden Viewport eine grafische Darstellung der Funktion
![]()
gezeichnet. Dabei werden alle vier Varianten der Koordinatenrichtungen gezeigt.
Nach dem Start des Beispiel-Programms c_usercoords.html ist zunächst "anisotrope Skalierung" eingestellt, und man sieht das nebenstehende Bild: In den vier Viewports der oberen Reihe wird auf die Vorgabe eines "Randes" verzichtet, so dass beide Viewport-Richtungen bei anisotroper Skalierung voll genutzt werden, in der unteren Reihe wird ein Rand von 10% der Viewport-Abmessungen vorgesehen, so dass die Punkte, mit denen die "User coordinates" definiert werden, nicht mehr in den Viewport-Ecken liegen.
Im Body-Teil der HTML-Datei wird der Canvas-Bereich mit der id="canvas" erzeugt, die Zeichenaktion wird gestart durch eine Anweisung im Body-Tag:
<body onLoad="init();">
In der JavaScript-Funktion init wird das cavasGI-Objekt erzeugt und einer global vereinbarten Variablen gi zugewiesen, damit es in allen anderen Funktionen verfügbar ist:
var gi ;
var isotrop = false ;
function init() {
gi = new canvasGI ("canvas") ; // ... definiert ein canvasGI-Objekt
draw () ;
}
Im zweiten Schritt startet init die Funktion draw, in der die Viewports definiert und alle Zeichenaktionen ausgeführt werden (die farbig gekennzeichneten Bereiche werden weiter unten erläutert):
function draw() {
var nViewpx = 4 , nViewpy = 2 , pmarg = 0 ;
var ix , iy , x ;
var canwidth = gi.getcanvaswidth () ;
var canheight = gi.getcanvasheight () ;
gi.clearcanvas ("cyan") ;
for (iy = 0 ; iy < nViewpy ; iy++) {
for (ix = 0 ; ix < nViewpx ; ix++) {
gi.setcurrentviewport (canwidth * ix / nViewpx , canheight * iy / nViewpy ,
canwidth / nViewpx , canheight / nViewpy , gi.XYBOTTOMLEFT) ;
// ... definiert den "Current viewport" mit einem Viewport-
// Koordinatensystem in der linken unteren Ecke
gi.vdrawrect (2 , canheight / nViewpy - 2 , canwidth / nViewpx - 4 , canheight / nViewpy - 4 , "black") ;
// ... zeichnet schwarzen Rahmen um jeden Viewport, 2 Pixel nach innen gerueckt
gi.beginpath () ; // ... startet einen "Path"
if (isotrop == false) {
switch (ix) {
case 0: gi.setusercoordsa ( 0. , -3.5 , 10.5 , 4.5 , pmarg) ; break ;
// ... definiert "User coordinates": Punkt (0;-3.5) wird auf die
// linke untere Viewport-Ecke gelegt, Punkt (10.5;4.5) auf
// die rechte obere Ecke (da die Werte keinen Bezug auf die
// Viewport-Abmessungen nehmen, werden die beiden Achsen im
// Regelfall unterschiedlich skaliert), bei ix=0 (obere
// Reihe) gilt pmarg=0. (kein Rand), danach pmarg=10.
case 1: gi.setusercoordsa ( 0. , 4.5 , 10.5 , -3.5 , pmarg) ; break ;
case 2: gi.setusercoordsa (10. , 4.5 , 0. , -3.5 , pmarg) ; break ;
case 3: gi.setusercoordsa (10. , -3.5 , 0. , 4.5 , pmarg) ; break ;
}
}
else { // ... und nun fuer isotrope Skalierung
switch (ix) {
case 0: gi.setusercoordsi ( 0. , -3.5 , 10.5 , 4.5 , pmarg) ; break ;
case 1: gi.setusercoordsi ( 0. , 4.5 , 10.5 , -3.5 , pmarg) ; break ;
case 2: gi.setusercoordsi (10. , 4.5 , 0. , -3.5 , pmarg) ; break ;
case 3: gi.setusercoordsi (10. , -3.5 , 0. , 4.5 , pmarg) ; break ;
}
}
// ... und in den vier Viewports einer Reihe sind alle vier
// Kombinationen fuer die Richtungen der beiden
// Koordinatenachsen realisiert
gi.umoveto ( 0. , 4.5) ;
gi.ulineto ( 0. , -3.5) ; // Horizontale Linie als x-Achse
gi.umoveto ( 0. , 0. ) ;
gi.ulineto (10.5 , 0. ) ; // Vertikale Linie als y-Achse
gi.umoveto ( 0. , 4. ) ; // Startpunkt fuer Funktionsgraph
for (x = 0.05 ; x <= 10. ; x += 0.05) {
// -x/5
// Funktion y = 4 e cos 3x :
gi.ulineto (x , 4. * Math.exp (-.2 * x) * Math.cos (3. * x)) ;
}
gi.stroke () ; // ... zeichnet den definierten "Path"
} // ... Ende einer Reihe
pmarg = 10 ; // ... Rand (10%) fuer die Viewports der unteren Reihe
} // ... Ende aller Reihen
} // ... Ende function draw
- Mit gi.getcanvaswidth und gi.getcanvasheight werden die Abmessungen der Zeichenfläche vom CanvasGI abgefordert. Das ist prinzipiell nicht erforderlich, denn der Programmierer kennt ja die von ihm selbst im <canvas>-Tag festgelegten Abmessungen. Wenn er sie dort allerdings ändert, braucht er keine Änderung an anderer Stelle vorzunehmen.
- Mit gi.clearcanvas wird die Zeichenfläche mit Hintergrundfarbe gefüllt.
- Mit gi.setcurrentviewport werden die Viewports mit einheitlicher Höhe und Breite so definiert, dass die Zeichenfläche von den insgesamt 8 Viewports komplett gefüllt wird. Der optionale 5. Parameter legt hier mit gi.XYBOTTOMLEFT den Ursprung des Koordinatensystems in die jeweilige linke untere Viewportecke (mit nach rechts und oben gerichteten Achsen). Auf dieses Koordinatensystem muss sich die nachfolgende Funktion vdrawrect beziehen.
- Der Aufruf von gi.vdrawrect (v steht für "Viewport coordinates", draw für sofortige Zeichenaktion) zeichnet einen schwarzen Rahmen um den jeweiligen Viewport.
- Mit gi.beginpath wird für jeden Viewport ein "Drawing path" gestartet, in dem alle weiteren Ausgaben für den Viewport gesammelt werden, die schließlich, wenn die Aktionen für den Viewport komplett sind, mit gi.stroke gezeichnet werden.
- Mit gi.setusercoordsa bzw. gi.setusercoordsi werden die (anisotrop bzw. isotrop zu skalierenden) "User coordinates" für alle Viewports definiert.
- Die Anweisungen gi.umoveto bzw. gi.ulineto beziehen sich auf die für die Viewports definierten "User coordinates" (diese Funktionen beginnen immer mit u). Beide Funktionen lösen keine unmittelbaren Aktionen aus, werden nur im "Path" gesammelt, und erst beim nachfolgenden gi.stroke wird gezeichnet.
- Nachdem die obere Viewport-Reihe gezeichnet wurde, wird der Wert für die Variable pmarg, der mit 0 initialisiert wurde, auf 10 gesetzt, was dazu führt, dass in der unteren Reihe in allen Viewports ein Rand von 10% der Viewport-Abmessungen berücksichtigt wird.
Beispiel-Programm (isotrope Skalierung)
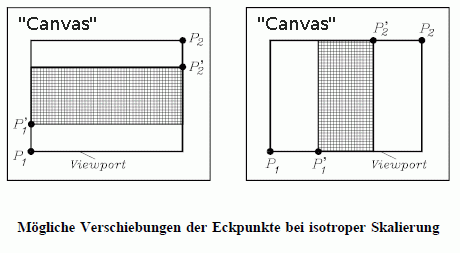
Wenn "isotrope Skalierung" gefordert wird ("User coordinates" werden mit setusercoordsi definiert), werden die beiden Punkte P1 und P2, die die "User coordinates" definieren, so verändert, dass sich in beiden Koordinatenrichtungen gleiche Skalierungen ergeben. Dabei bleibt in der Regel in einer Richtung ein Teil des Viewport-Bereichs ungenutzt. Das Koordinatensystem wird automatisch so gelegt, dass die Distanz der beiden Punkte in dieser Richtung in die Mitte des Viewports fällt.
Die nebenstehende Abbildung zeigt die beiden Möglichkeiten der Platzierung des Zeichenbereichs im Viewport in Abhängikeit davon, welche Richtung durch den von den "User coordinates" abzubildenden Bereich besser auszufüllen ist.
Auch für die isotrope Skalierung kann ein Randbereich festgelegt werden. In diesem Fall wird die Distanz der Punkte P1 und P2 in der "ungünstigeren Richtung" auf jeder Seite um pmarg Prozent vergrößert. In der anderen Richtung liegt der Zeichenbereich auch in diesem Fall in der Viewportmitte.
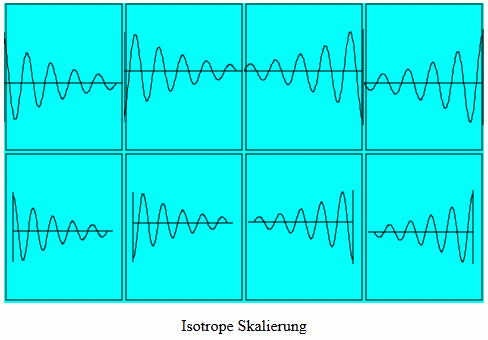
Das Beispiel-Programms c_usercoords.html, das mit anisotroper Skalierung startet, bietet einen Button zum Umschalten auf isotrope Skalierung an. Danach sieht man die Viewports entsprechend nebenstehender Abbildung.
Weiterlesen
Folgende Seiten werden als Einführung in die Benutzung des CanvasGI empfohlen:
- Empfehlung zum Weiterlesen: "Marker zeichnen" für das Zeichnen an "User coordinates"-Positionen,
- "Skelett-Seite" für die Nutzung des CanvasGI-Interfaces und die JavaScript-Datei mit den Interface-Routinen,
- Farben in CanvasGI,
- "Viewports und Clipping", isotrope und anisotrope Skalierung.

