Besonderheiten der 3D-Transformationen
Es wird (wie im Fall der ebenen Transformation) die so genannte geometrische Transformation betrachtet, bei der ein Objekt in einem festen Koordinatensystem bewegt wird.
Es genügt, das "Schicksal" eines Punktes bei einer Transformation zu untersuchen. In allen Fällen wird im Folgenden die "alte" Lage des Punktes durch die Koordinaten x, y und z beschrieben, die Lage nach der Transformation durch die Koordinaten x', y' und z'.
Nachfolgend werden die Transformationsformeln für die geometrische Transformation eines 3D-Punktes angegeben. Es gelten alle Aussagen, die auf der Seite "Ebene Transformationen" gemacht wurden, insbesondere die Aussagen zur zusammengesetzten Transformation, zusätzlich ist zu beachten:
- Die Rotation bedeutet im Raum immer "Rotation um eine vorzugebende Achse" (das gilt natürlich auch für die Ebene, dort ist von der Rotationsachse aber immer nur ein Punkt zu sehen). Als "elementare Rotationen" werden die Rotationen um die drei Koordinatenachsen betrachtet (im Gegensatz zu einer "Elementar-Rotation" in der Ebene, der Rotation um den Nullpunkt). Rotationen um beliebige Achsen sind durch "Verknüpfung von Transformationen" zu realisieren.
- Um die im Raum besonders wichtigen Verknüpfungen von Transformationen einheitlich (durch Multiplikation von Matrizen) realisieren zu können, sollte unbedingt mit "homogenen Koordinaten" gearbeitet werden. Nachfolgend werden die Transformationsformeln deshalb auch nur unter Verwendung homogener Koordinaten zusammengestellt.
Geometrische 3D-Transformationen mit homogenen Koordinaten
Die nachfolgend angegebenen Formeln sind im CanvasGI für die 3D-Transformationen realisiert:
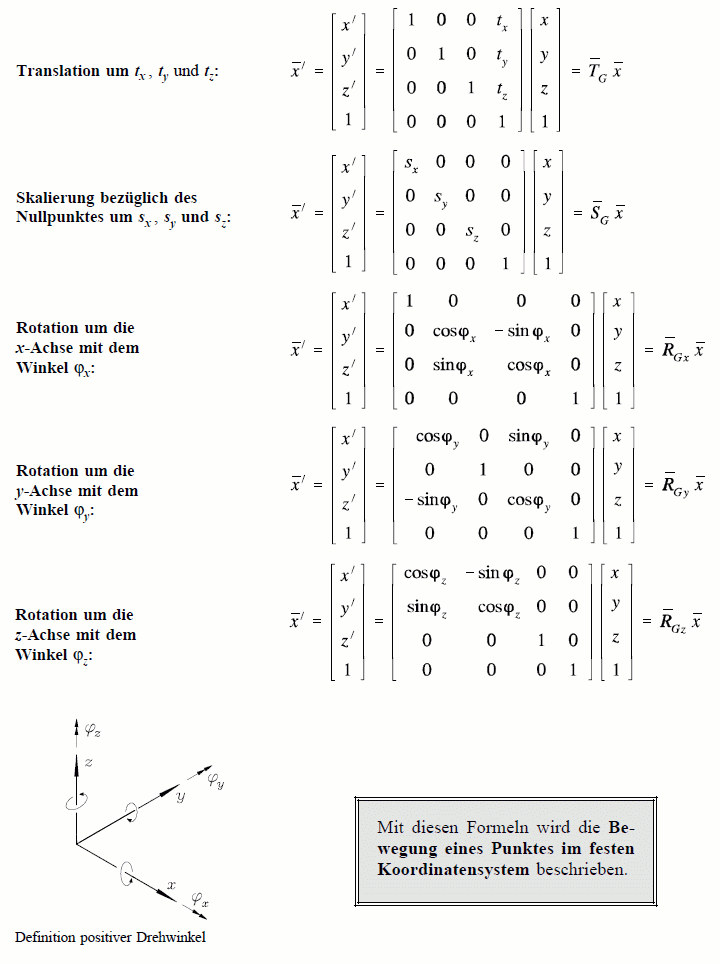
Verknüpfung von Transformationen
Aus den oben angegebenen Elementartransformationen können beliebige Transformationen durch das Ausführen von mehreren Transformationen nacheinander realisiert werden. Dabei ist zu beachten, dass eine Transformation immer durch Linksmultiplikation mit der entsprechenden Transformationsmatrix realisiert wird, so dass schließlich ein Produkt mehrerer Transformationsmatrizen die Gesamt-Transformation beschreibt, bei der die Matrix der letzten Transformation links steht.
Man beachte, dass eine Vertauschung der Reihenfolge zweier Transformationen in der Regel auf eine ganz andere Gesamt-Transformation führt. In der mathematischen Beschreibung verknüpfter Transformationen mit homogenen Koordinaten wird dies durch die Matrizen-Produkte der Transformationsmatrizen deutlich: Im Gegensatz zum Produkt skalarer Größen ist das Matrix-Produkt nicht kommutativ.
Das CanvasGI enthält stets eine Transformationsmatrix für die ebene Transformation und eine Transformationsmatrix für die 3D-Transformation. Beide Matrizen werden als Einheitsmatrizen initialisiert, so dass zunächst keine Unterschiede bei der Verwendung der zeichnenden Funktionen, die die Transformation auswerten, und den "gewöhnlichen" Zeichenfunktionen bestehen. Erst dann, wenn mit den entsprechenden Funktionen eine Transformation geändert wurde, macht sich dies (nur) bei den speziellen Zeichenfunktionen bemerkbar. Die Namen der Zeichenfunktionen, die die 3D-Transformation auswerten, beginnen alle mit wt... bzw. wtdraw..., ein ausführlicher erläutertes Beispiel findet man auf der Seite, die nachfolgend als "Empfehlung zum Weiterlesen" angegeben ist.
Weiterlesen
Auf der folgenden Seite werden die hier beschriebenen Transformationen mit den Projektionen verknüpft:
- Empfehlung zum Weiterlesen: "Projektionen und Transformationen, Beispielprogramm "Projektion 2"".
Folgende Seiten werden als Einführung in die Benutzung der 3D-Grafik mit CanvasGI empfohlen:

