Mathematische Beschreibung der 3D-Flächen
Die einfachste Beschreibung einer 3D-Fläche ist die Angabe einer Funktion
z = z (x , y) ,
so dass jedem Punkt der x-y-Ebene eine "Höhe" z zugeordnet wird. Die Menge aller Koordinaten-Tripel, die auf diese Weise gebildet werden können, beschreibt die Fläche.
Allerdings sind komplizierte Flächen (insbesondere solche, bei denen zu einem Wertepaar in der x-y-Ebene mehrere Flächenpunkte gehören) kaum auf diesem Wege beschreibbar. Diese sollten unbedingt in Parameterdarstellung beschrieben werden. Zwei unabhängigen Variablen u und v, die in einem vorzugebenen Bereich variieren dürfen, sind drei Berechnungsvorschriften für die Koordinaten x, y und z zuzuordnen:
x = x (u , v) ; y = y (u , v) ; z = z (u , v)
definieren die Fläche im Bereich
umin ≤ u ≤ umax ; vmin ≤ v ≤ vmax .
Die beim Start der Seite nebenstehend zu sehende "Helix" ist zum Beispiel so definiert:
x = u cos v ; y = u sin v ; z = v/4
im Bereich
1 ≤ u ≤ 3 ; −4π ≤ v ≤ 4π .
Mit einem kleinen Trick können auch Funktionen, die in der Form z = z (x , y) definiert sind, in das gleiche Schema eingepasst werden, indem x = u und y = v gesetzt wird und dann z (u , v) aufgeschrieben wird. Die Funktion
z = cos (x·y)
(Klicken auf den Button mit dieser Beschriftung zeigt die zugehörige 3D-Fläche) ist intern als
x = u ; y = v ; z = cos (u·v)
definiert.
Die oben rechts zu sehende Grafik wurde wie folgt realisiert:
- Im Body-Teil der HTML-Datei wird der Canvas-Bereich mit der id="canvas"
erzeugt, die Zeichenaktion wird gestartet durch eine Anweisung im Body-Tag:
<body onLoad="init();">
- In der JavaScript-Funktion init wird das CavasGI-Objekt erzeugt und einer global vereinbarten Variablen gi zugewiesen, damit es in allen anderen Funktionen verfügbar ist:
function init () {
gi = new canvasGI ("canvas") ; // Ein "CanvasGI-Objekt" wird erzeugt
gi.setcurrentviewport (0 , 0 , gi.getcanvaswidth() , gi.getcanvasheight () , gi.XYBOTTOMLEFT) ;
newModel (2) ;
phiplus (gi.AXIS_X) ;
}
- Mit der CanvasGI-Funktion setcurrentviewport wird die gesamte Zeichenfläche als "Current viewport" eingestellt, was eigentlich nicht erforderlich ist (Standardeinstellung), aber das Viewport-Koordinatensystem wird in die linke untere Ecke verlegt, so dass die Textausschrift einfacher zu positionieren ist.
- Mit der Funktion newModel wird der Aufbau des darzustellenden Modells gestartet (die 2 als Parameter steht für die "Helix", die beim Start der Seite zu sehen ist). Es ist ein "Flächenmodell" (siehe Seite "Einfache 3D-Modelle"), dessen Erzeugung weiter unten beschrieben wird.
- Schließlich wird mit der Funktion phiplus (wird auch weiter unten gelistet und beschrieben) die Animation gestartet.
Es können 8 verschiedene 3D-Flächen gewählt werden. Ihre Parameter sind in einem Array models zusammgestellt, die Berechnung des Koordinatentripels eines Punktes wird von einer Funktion xyzvonuv realisiert, von der nachfolgend nur das Erzeugen der Punktkoordinaten für das Hyperboloid ("case 0") gelistet wird:
var models = [["Hyperboloid" , 0 , 2*Math.PI , -2 , 2 , 40 , 20 , 1 , 1 , 1 , 1] ,
["Torus" , 0 , 2*Math.PI , 0 , 2*Math.PI , 20 , 90 , 4 , 1] ,
["Helix" , 1 , 3 , -4*Math.PI , 4*Math.PI , 10 , 200 , 0.25] ,
["Kreishelix" , 0 , 2*Math.PI , -6*Math.PI , 2*Math.PI , 20 , 200 , 5 , 2 , 0.8] ,
["Rotoide" , 0 , 2*Math.PI , 0 , 4*Math.PI , 12 , 540 , 4 , 1.5 , 0.4 , 8.5] ,
["Parabelschnecke" , -1 , 1 , 0 , 8*Math.PI , 20 , 240 , -1 , 2 , 0.17 , 30] ,
["z = xy" , -1 , 1 , -1 , 1 , 20 , 20 , 1] ,
["z = cos(xy)" , -3 , 3 , -3 , 3 , 50 , 50 , 1 , 1]] ;
// Fuer jedes Modell: Name, umin, umax, vmin, vmax, nu, nv, p1, p2, ...
function xyzvonuv (u , v) {
switch (actfun) {
case 0 :
var a = models[actfun][7] ;
var b = models[actfun][8] ;
var c = models[actfun][9] ;
var d = models[actfun][10] ;
return [ a * Math.sqrt(d + v*v) * Math.cos(u) ,
b * Math.sqrt(d + v*v) * Math.sin(u) ,
c * v ] ;
case 1 : // ...
Ein Flächenmodell besteht aus dem Koordinatenfeld xyz mit Koordinatentripeln für alle Punkte des Modells und dem Feld area, in dem für alle Flächen die zugehörigen Punkte im Koordinatenfeld verzeichnet sind. Die Parameterbereiche für u und v werden in xusteps bzw. yvsteps Streifen gleicher Breite unterteilt, so dass xusteps·yvsteps Flächen (Vierecke) entstehen. In der Funktion pointsandareas werden die Arrays aufgebaut:
function pointsandareas () {
var u = xu1 , v = yu1 , ixy = 0 ; iarea = 0 ;
var du = (xu2 - xu1) / xusteps ;
var dv = (yu2 - yu1) / yvsteps ;
for (var i = 0 ; i < xusteps ; i++) {
v = yu1 ;
for (var j = 0 ; j < yvsteps ; j++) {
area[iarea++] = [ixy , ixy + 1 , ixy + 2 , ixy + 3 , "red"] ;
xyz[ixy++] = xyzvonuv (u , v) ;
xyz[ixy++] = xyzvonuv (u + du , v) ;
xyz[ixy++] = xyzvonuv (u + du , v + dv) ;
xyz[ixy++] = xyzvonuv (u , v + dv) ;
v += dv ;
}
u += du ;
}
area.length = xusteps * yvsteps ; // ... Array koennte kleiner geworden sein
xyz.length = area.length * 4 ;
gi.areacol (area , xyz) ; // ... ersetzt Farbe ("red") durch Farbverlauf
}
- In einer doppelten Schleife werden zunächst die Flächen (Array area) definiert, indem fortlaufende Punktnummern (jeweils 4 für eine Fläche) eingesetzt werden, für die nachfolgend 4 Koordinatentripel in das Array xyz eingesetzt werden. Dies ist nicht speicheroptimal (Punkte gehören zu zwei bis vier Flächen), aber einfach zu programmieren.
- Die in das Array xyz einzusetzenden Koordinatentripel werden jeweils
mit einem Aufruf der oben beschriebenen Funktion xyzvonuv erzeugt.
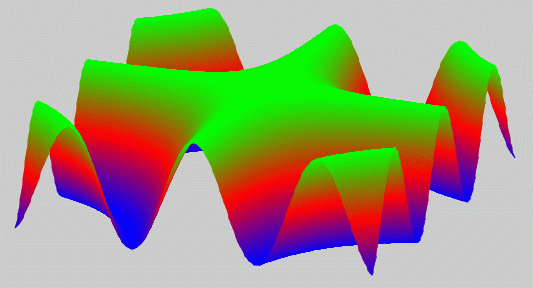
- Der letzte Parameter in einer Flächenbeschreibung ist jeweils die Farbe, mit der die Fläche dargestellt werden soll. Die hier (in der weißen Zeile) zunächst eingetragene Farbe "rot" wird für alle Flächen in der grün gekennzeichneten Zeile überschrieben und durch einen "Farbverlauf" über alle Flächen ersetzt (realisiert von der CanvasGI-Funktion areacol). Die Funktion areacol generiert die Farben in Abhängigkeit von der z-Koordinate, so dass die am weitesten oben liegenden Flächen grün sind, im Mittelbereich rote Flächen erscheinen und die am weitesten unten liegenden Flächen blau sind. Das ist ziemlich willkürlich, erfüllt aber den Zweck, die Krümmungen der Gesamtfläche zu verdeutlichen (nebenstehendes Beispiel).
Schließlich muss das Modell noch gezeichnet werden: Aus der Funktion init (siehe oben) wird die Funktion newModel aufgerufen, die mit pointsandareas das Modell erzeugt und die Funktion Fit startet. Diese berechnet die Grenzen der Darstellung in der 2D-Zeichenfläche (mit der CanvasGI-Funktion ptlimits) und stellt die Zeichenfläche mit der CanvasGI-Funktion setusercoordsi passend ein. Danach wird die Funktion draw gestartet, die die auf der Seite "3D-Flächenmodelle in geeigneter Reihenfolge zeichnen" ausführlich besprochene Strategie realisiert (Berechnen eines "symbolischen Abstands" aller Flächen vom Betrachter, Sortieren der Flächen nach diesem Abstand und Zeichnen in der sortierten Reihenfolge "von hinten nach vorn"). Die Funktion wird hier deshalb nur gelistet und nicht weiter kommentiert:
function draw () {
var points = new Array () ; // ... fuer die Koordinaten eines Polygons
gi.clearcanvas ("silver" , "black") ; // ... fuellt Canvas-Bereich mit Hintergrundfarbe
for (var i = 0 ; i < area.length ; i++) {
var np = area[i].length - 1 ; // ... weil letztes Element die Farbe ist
for (var j = 0 ; j < np ; j++) {
points[j] = xyz[area[i][j]] ; // ... sammelt Punktkoordinaten eines Polygons
}
area[i].unshift (gi.wtsymbdist (points , np)) ; // ... berechnet symbolischen Abstand vom Betrachter
} // und fuegt diesen Wert an der Array-Spitze an
gi.sortbyindex (area , 0) ; // ... sortiert nach den Werten an der Array-Spitze
for (var i = 0 ; i < area.length ; i++) { // ... zeichnet alles in der korrekten Reihenfolge
area[i].shift() ; // ... entfernt den Wert an der Array-Spitze wieder
var np = area[i].length - 1 ;
for (var j = 0 ; j < np ; j++) {
points[j] = xyz[area[i][j]] ; // ... sammelt Punktkoordinaten eines Polygons
}
gi.wtdrawfarea (points , np , area[i][np] , "black") ; // ... zeichnet ein einzelnes Polygon
}
gi.vdrawtext (models[actfun][0] , 10 , 10 , "black" , "16pt sans-serif") ;
}
Die letzte Aktion in der Start-Funktion init ist der Aufruf der Funktion phiplus. Diese startet mit window.setInterval sofort eine Animation, indem alle dT Tausendstel-Sekunden (dT ist global mit dem Wert dT = 50 vereinbart) die Funktion rotation gestartet wird:
function rotation () {
gi.t3rotation (dPhi , rotax) ;
draw () ;
}
function phiplus (axis) {
rotax = axis ;
if (anim == 1) {
window.clearInterval (aktiv) ;
}
anim = 1 ;
aktiv = window.setInterval("rotation ()" , dT);
}
- In der (ständig aufgerufenen) Funktion rotation wird mit der CanvasGI-Funktion t3rotation bei jedem Aufruf eine (zusätzliche) Rotations-Transformation um die jeweils vorgegebene Achse eingestellt. Die anschließend aufgerufene Funktion draw benutzt dann die aktuelle Transformation.

Es ist ein aufwendiger Algorithmus, der hier beschrieben wurde. Wer diesen Satz gerade liest, hat das wahrscheinlich schon bemerkt, weil die oben zu sehende Animation etwas zögerlich läuft. Man denke an den Aufwand, der betrieben werden muss: Für die "Helix" werden 2000 Flächen erzeugt, nach dem "symbolischen Abstand" vom Betrachter sortiert und danach gezeichnet. Da ist es wohl verzeihlich, wenn der Computer es nicht schafft, für diese Aktion jeweils nur 50/1000 Sekunden zu benötigen, wie ihm von den vorgegebenen globalen Werte zugestanden wird.
Sicher kann man seinen Computer an die Grenze seiner Leistungsfähigkeit bringen, wenn man oben auf den Button "Rotoide" klickt, die nebenstehend als "Momentaufnahme" zu sehen ist. Die Parameter für diese Fläche sind so gewählt, dass die Schlingen erst "nach zwei Runden" die Ausgangslage wieder erreichen. Dementsprechend mussten für eine vernünftige Darstellung 6480 Teilfächen erzeugt werden.
Wenn auch diese Animation wie eine kontinuierlich ablaufende Bewegung aussieht, dann benutzt man gerade einen sehr schnellen Computer. Dieser Satz wurde im Februar 2013 geschrieben. Mal sehen, wann vielleicht sogar Smartphones diese Rotoide kontinuierlich bewegen können.
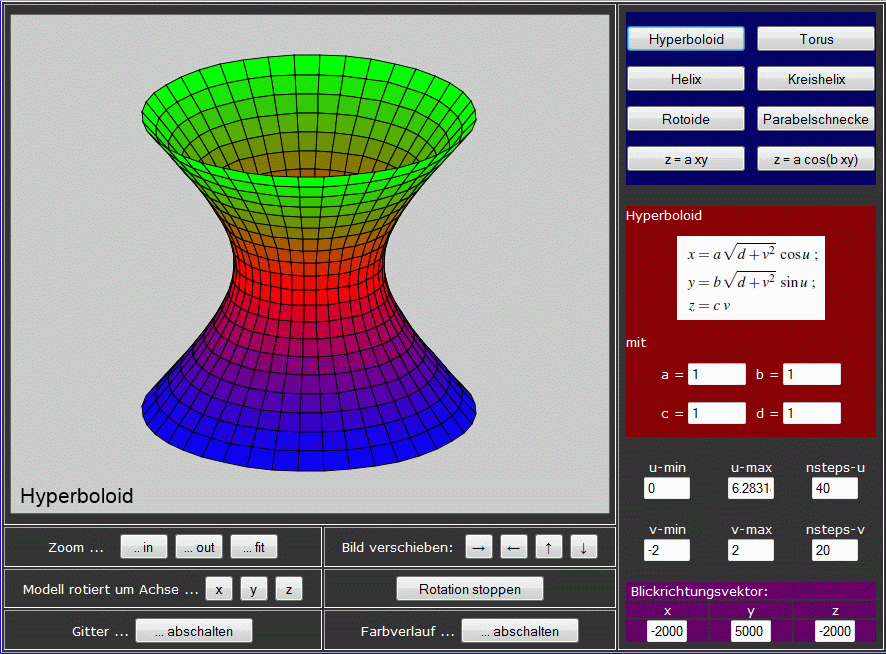
Beipiel-Programm "Mathematisch beschriebene 3D-Flächen"
Das Beispiel-Programm "Mathematisch beschriebene 3D-Flächen" enthält neben den oben beschriebenen Funktionen noch weitere Angebote. Es startet mit folgendem Bild:
Die wesentlichen Erweiterungen gegeüber der Grafik, die sich oben rechts auf der aktuellen Seite befindet, sind:
- Die mathematischen Gleichungen, die die dargestellte Fläche definieren, werden angegeben, zusätzlich die aktuellen Werte für die Parameter in den Gleichungen, die beliebig geändert werden können.
- Die Krümmung der Flächen wird verdeutlicht durch ein Gitter und einen Farbverlauf. Beides kann abgeschaltet werden, so dass man die Konsequenzen sieht.
- Der Blickrichtungsvektor kann geändert werden.
Weiterlesen
Dies ist das (vorläufige) Ende des als Tutorial angelegten Bereichs "CanvasGI". Folgende Seiten sollte man sich noch ansehen:
- Auf der Seite "CanvasGI - Beschreibung der verfügbaren Funktionen" findet man eine Zusammenstellung aller Funktionen, die auf den Seiten des Tutorials und in den Beispiel-Seiten verwendet wurden.
- Uber das oben zu findende Menüangebot "Beispiel-Seiten öffnen" findet man das Angebot aller Beispiele, auf die im Tutorial verwiesen wird.
- Es gibt einige weitere Beispiele, die man über die Seite "Technische Mechanik aktuell" erreichen kann: