Die "t...-Funktionen" und die "ut...-Funktionen" in CanvasGI
| Diese Animation ist das Ziel, das am Ende der Einführung in das Thema "Ebene Transformation" erreicht wird |
Die Funktionen in CanvasGI, die mit der ebenen Transformation korrespondieren, lassen sich in zwei Gruppen einteilen:
- Die "vorbereitenden t...-Funktionen" definieren bzw. ändern die gültige ebene Transformationsmatrix.
- Die "zeichnenden ut...-Funktionen" arbeiten wie die auf der Seite "Problembezogene Koordinatensysteme (User coordinates)" beschriebenen "u...-Funktionen" mit "User coordinates", beziehen sich auf das gültige (mit setusercoordsa bzw. setusercoordsi eingestellte) Koordinatensystem, wenden aber vor der eigentlichen Zeichenaktion die gültige ebene Transformationsmatrix auf die übergebenen Koordinaten an.
Nicht zu allen "u...-Funktionen" existieren auch die entsprechenden "zeichnenden ut...-Funktionen", konsequent kann das Prinzip der Vorab-Transformation ohnehin nur für die Argumente realisiert werden, die Punkt-Koordinaten beschreiben ("Move to", "Line to", "Polygon", ...). Die "ut...-Funktionen", mit denen Kreise bzw. Kreisbögen mit Mittelpunkt und Radius beschrieben werden, wenden auf den Radius z. B. nur die eingestellte Skalierung an.
Nachfolgend werden das Prinzip des Arbeitens mit den "t...-Funktionen" und den "ut...-Funktionen" und die Verwendung der wichtigsten Funktionen am Beispiel des Programms c_malteser.html (Zeichnen eines symbolischen Malteserkreuz-Getriebes) dargestellt, das schrittweise entwickelt wird.
Aufgabe, Zeichnen des Malteserkreuzes
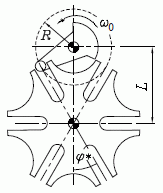
Die rechts zu sehende Skizze zeigt das Schema des Getriebes, das nach dem Prinzip arbeitet, das in der Animation oben zu sehen ist. Das Malteserkreuz der dargestellten Variante besteht aus 6 jeweils um 60° versetzten "Schwalbenschwänzen", die jeweils durch einen Schlitz mit halbkreisförmigem Grund getrennt sind. Der eingezeichnete Winkel hat für das Abmessungsverhältnis R/L = 0,5 den Wert φ* = 30°.

Es bietet sich also an, nur ein Sechstel des Bildes zu programmieren und mit geeigneten Rotationstransformationen wiederholt zu erzeugen. Die Abbildung links zeigt das zu programmierende Sechstel. Schon für das Erzeugen dieses Teilbildes werden mit Vorteil Rotationstransformationen eingesetzt (der Schlitz kann auf diese Weise in vertikaler Lage programmiert werden).
Im Body-Teil der HTML-Datei c_malteser.html wird der Canvas-Bereich mit der id="canvas" erzeugt, die Zeichenaktion wird gestart durch eine Anweisung im Body-Tag:
<body onLoad="init();">
In der JavaScript-Funktion init werden vorbereitend folgende Aktionen ausgeführt:
- Ein cavasGI-Objekt wird erzeugt und einer global vereinbarten Variablen gi zugewiesen, damit es in allen anderen Funktionen verfügbar ist:
- Mit gi.setusercoordsi werden "User coordinates" so definiert, dass die Koordinatenachsen nach rechts bzw. oben zeigen (die Abmessungen L, R und RS sind global vereinbart und werden weiter unten erläutert).
- Schließlich wird die Funktion draw gestartet, die den Zeichenbereich mit gi.clearcanvas mit Hintergrundfarbe und einem Rahmen füllt und die drei Funktionen crank, cross und pivots aufruft, die die Kurbel, das Malteserkreuz und die Lagersymbole zeichnen:
function draw () {
gi.clearcanvas ("silver" , "black") ; // ... fuellt Canvas-Bereich mit Hintergrundfarbe
// ("silver") und zeichnet schwarzen Rahmen
crank () ; // ... zeichnet die Kurbel
cross () ; // ... zeichnet das Malteserkreuz
pivots () ; // ... zeichnet die Lager
}
function init () {
gi = new canvasGI ("canvas") ; // Ein "CanvasGI-Objekt" wird erzeugt
gi.setusercoordsi (-L , -L , L , L+R+Rs) ;
draw () ;
}
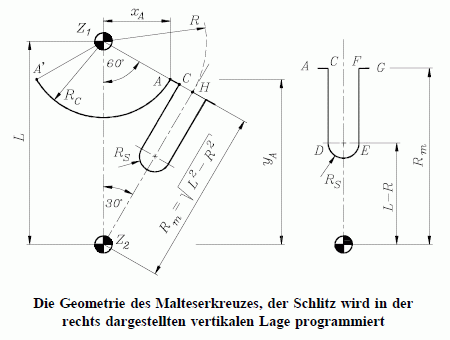
Zunächst wird nur die Funktion cross betrachtet, die das Malteserkreuz erzeugt. Um den nachfolgenden Ausschnitt aus dem Programmcode besser zu verstehen, zeigt die nebenstehende Skizze die typischen Abmessungen, die die Geometrie des Malteserkreuzes bestimmen:
Die Mittelpunkte der beiden Drehzapfen Z1 und Z2 bilden mit dem Punkt H ein rechtwinkliges Dreieck. Die eingezeichneten Winkel und die Abmessungen L, R, RC und RS definieren die aus Kreisbögen und Geraden aufgebaute Kontur. Das Koordinatensystem wurde so definiert, dass es sinnvoll ist, den unteren Drehzapfen in den Nullpunkt zu legen.
Alle Abmessungen werden als globale Variablen vereinbart, so dass sie in allen Funktionen verfügbar sind.
Die einzelnen Anweisungen der Funktion cross werden nachfolgend erläutert (die "vorbereitenden t...-Funktionen" sieht man in grüner Farbe, die "zeichnenden ut...-Funktionen" sind hellblau):
function cross () {
gi.tinit () ;
gi.beginpath () ;
for (var i = 0 ; i < 6 ; i++) {
gi.utarc (0 , L , Rc , 5*Math.PI/6 , Math.PI/6 , true);
gi.trot (0 , 0 , -Math.PI/6) ; // ... Rotation um 30° im Uhrzeigersinn
gi.utlineto (-Rs , Rm) ;
gi.utlineto (-Rs , L - R) ;
gi.utarc (0 , L - R , Rs , Math.PI , 0 , true);
gi.utlineto ( Rs , Rm) ;
gi.trot (0 , 0 , -Math.PI/6) ; // ... und noch einmal 30°
gi.utlineto (-xA , yA) ;
}
gi.fillstyle ("blue") ;
gi.fill () ;
gi.stroke () ;
}
- Mit tinit wird die Transformationsmatrix (als Einheitsmatrix) initialisiert, so dass alle "ut...-Funktionen" zunächst wie die entsprechenden "u...-Funktionen" arbeiten (keine Transformation).
- Mit der Funktion wird eine (zusätzliche) Rotations-Transformation mit dem Winkel phi um den Drehpunkt (xM,yM) eingestellt. Der Winkel ist positiv, wenn gegen den Uhrzeigersinn gedreht wird (mit −Math.PI/6 wird also eine Rechtsdrehung um 30° erreicht).
- Mit der Funktion
utarc (xM , yM , r , phi1 , phi2 , anticlock)
wird das Zeichnen eines Kreisbogens definiert (alle in diesem Beispiel verwendeten Zeichenfunktionen sind in einen "Path" einzufügen und zeichnen erst mit dem stroke-Aufruf). (xM,yM) ist der Mittelpunkt des Kreisbogens, der der jeweils eingestellten Transformation unterworfen wird, r sein Radius. Gezeichnet wird von Winkel phi1 bis Winkel phi2 entgegen dem Uhrzeigersinn, wenn anticlock den Wert true hat, ansonsten im Uhrzeigersinn.Dies entspricht der etwas gewöhnungsbedürftigen Philosophie, wie die "Canvas"-Funktion arc arbeitet. Man beachte, dass zusätzlich zum Startpunkt des Kreisbogens eine gerade Linie gezogen wird, wenn es nicht (wie hier beim ersten Aufruf) die erste Aktion in einem "Path" ist. Ansonsten endet in diesem Beispiel jede vorausgehende Aktion am Startpunkt der nachfolgenden Aktion.
- Man beachte den kleinen (aber wichtigen) Trick, dass der Schlitz so gezeichnet wird, als wäre er in vertikaler Lage. Das ist möglich, weil vorher der Aufruf von trot eine Rotation um 30° nach rechts eingestellt hat.
- Mit der Funktion wird eine gerade Linie von der jeweils aktuellen Position (Endpunkt der vorangegangenen Aktion) zum Punkt (x,y) gezeichnet. Dieser Punkt wird natürlich auch vorab transformiert.
- Man beachte, dass der zweite Aufruf von trot eine zusätzlich Rotations-Transformation um noch einmal 30° bewirkt, so dass dem letzten utlineto-Aufruf die Koordinaten des Startpunktes des nachfolgenden Sechstels des Malteserkreuzes übergeben werden können.
- Alle Aktionen sind in eine Schleife eingebettet, die sechsmal durchlaufen wird. Weil sich am Ende eines Schleifendurchlaufs die Rotations-Transformationen zum Winkel von 60° addiert haben, wird mit dem nachfolgenden Durchlauf jeweils das nächste Sechstel gezeichnet.
Zeichnen der Kurbel und der symbolischen Drehzapfen
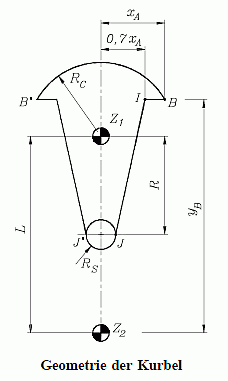
Natürlich wird die Kurbel (in der Funktion crank) auch in der nebenstehend dargestellten vertikalen Stellung programmiert, um sie durch eine vorangestellte Transformation um den Winkel phi0 = −Math.PI/3 im Uhrzeigersinn (grüne Zeile im folgenden Listing) in der gewünschten Lage erscheinen zu lassen (phi0 ist wie die Abmessungen als globale Variable definiert):
function crank () {
gi.tinit () ;
gi.beginpath () ;
gi.trot (0 , L , phi0) ; // ... Rotation im Uhrzeigersinn
gi.utarc (0 , L , Rc , 7*Math.PI/6 , 11*Math.PI/6 , false); // ... oberer
gi.utlineto (xA*0.7 , yB) ; // Bogen
gi.utlineto ( Rs , L - R) ;
gi.utlineto (-Rs , L - R) ;
gi.utlineto (-xA*0.7 , yB) ;
gi.closepath () ;
gi.fillstyle ("maroon") ;
gi.fill () ;
gi.stroke () ;
gi.utdrawfcirc (0 , L - R , Rs , "red") ; // ... Mitnehmer
}
|
- Das Zeichnen der Kontur ist in einen "Path" eingebettet und beginnt mit dem oberen Kreisbogen. Damit umgeht man das Problem, mit einem utmoveto zum Startpunkt des Bogens beginnen zu müssen (utarc als erste Funktion im "Path" legt den Startpunkt selbst fest, die Punktkoordinaten des Punktes B' müssten ansonsten mit Winkelfunktionen berechnet werden).
- Von Punkt J bis J ' müsste eigentlich auch ein Kreisbogen gezeichnet werden. Weil der Mitnehmer ohnehin mit einem gefüllten Kreis gezeichnet wird, kann diese Strecke mit einer dann verschwindenden Geraden überbrückt werden.
- Für die letzte gerade Linie, die zum Punkt B' führt, wird mit einem kleinen Trick auch hier das Berechnen der Punktkoordinaten vermieden: Wenn man einen "Path" mit closepath schließt, wird automatisch eine Gerade vom letzten Punkt zum Startpunkt gezeichnet.
- Nach dem Schließen wird der "Path" mit Farbe gefüllt (stroke zeichnet außerdem die Kontur), und mit utdrawfcirc wird ein mit roter Farbe gefüllter Kreis gezeichnet. Diese Funktion ist nicht in einen "Path" einzubetten (Name beginnt mit "utdraw"), sie zeichnet automatisch selbst.
Bleibt noch das Zeichnen der beiden symbolischen Drehzapfen, das in der Funktion pivots erledigt wird. Hierfür wird keine Transformation benötigt, deshalb kann eine "u...-Funktion" verwendet werden:
function pivots () {
var phi1 = 0 ;
var yM = 0 ; // ... Mittelpunkt des unteren Lagers
var fillcol = "black" ;
for (var j = 0 ; j < 2 ; j++) {
for (var i = 0 ; i < 4 ; i++) {
gi.udrawfpie (0 , yM , 0.9*Rs , phi1 , phi1 + Math.PI/2 , fillcol , "black") ;
phi1 += Math.PI/2 ;
fillcol = (fillcol == "yellow") ? "black" : "yellow" ;
}
phi1 = 0 ;
yM = L ; // ... Mittelpunkt des oberen Lagers
}
}
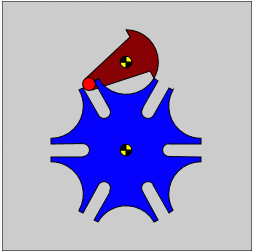
- Die äußere Schleife in dieser Funktion wird zweimal durchlaufen, wobei nur durch Änderung der Variablen yM vom unteren zum oberen Drehzapfen gewechselt wird.
- Die viermal zu durchlaufende innere Schleife zeichnet abwechselnd (mit schwarzer bzw. gelber Farbe) gefüllte Kreissektoren. Die Funktion zeichnet ein solches "Tortenstück" mit dem Mittelpunkt (xu,yu) und dem Radius r von Winkel phi1 bis Winkel phi2 (im Uhrzeigersinn), füllt es mit der Farbe fillcol und zeichnet die Kontur mit der Farbe strokecol. Diese Funktion wird nicht in einen "Path" eingebettet (Name beginnt mit "udraw"), sie zeichnet direkt.
Die komplette HTML-Datei c_malteser.html kann in einem neuen Browser-Fenster ausgeführt werden. Sie liefert mit den hier beschriebenen Funktionen das nebenstehend zu sehende Bild.
Weiterlesen
Folgende Seiten werden als Einführung in die Thematik "Transformationen" empfohlen:
- Empfehlung zum Weiterlesen:" Animation der Bewegung eines Malteserkreuzes".
- "Transformationen, homogene Koordinaten",
- "Ebene Transformationen".

