Zentralprojektion
- dem "Eye point" (Projektionszentrum), beschrieben durch einen Vektor c,
- der Projektionsebene, die durch einen Referenzpunkt (Vektor r0) und einen Normalenvektor n beschrieben wird,
- und einem so genannten "Up vector" uv zur Definition des ebenen u-v-Koordinatensystems der Bildebene.
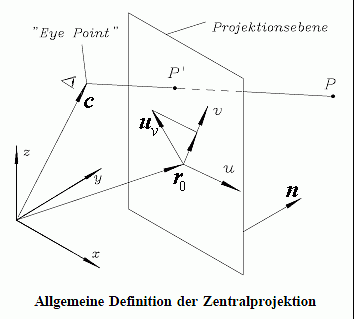
Die Vektoren c, r0, n und uv werden in einem dreidimensionalen raumfesten x-y-z-Koordinatensystem ("World coordinates") beschrieben, für den Vektor n wird vereinbart, dass er zu der Seite der Projektionsebene zeigt, auf der der "Eye point" nicht liegt.
Das zweidimensionale Koordinatensystem der Bildebene definiert sich wie folgt:
- Der Ursprung fällt mit dem Referenzpunkt zusammen.
- Die Richtung der v-Achse wird durch die Projektion des "Up vectors" auf die Projektionsebene festgelegt.
- Die Richtung der u-Achse wird so festgelegt, dass u, v und n in dieser Reihenfolge ein Linkssystem definieren ("Eye point" befindet sich vor dem Bildschirm, n zeigt in den Bildschirm hinein und das u-v-Koordinatensystem liegt in der Bildschirmebene wie die ebenen "User coordinates", wenn die Projektion des uv-Vektors auf dem Bildschirm vertikale Richtung hat).
Ein beliebiger Körperpunkt P, der im dreidimensionalen x-y-z-Koordinatensystem durch einen (in der Skizze nicht gezeichneten) Vektor p beschrieben wird und sowohl vor oder hinter und auch in der Projektionsebene liegen darf, wird auf die Projektionsebene abgebildet, indem der Schnittpunkt P' (nachfolgend durch den Vektor p' beschrieben) berechnet wird, den der Sehstrahl, der vom "Eye point" zum Punkt P gezogen wird, mit der Projektionsebene hat.
Da die Koordinaten des Punktes P' für den Zeichenvorgang im ebenen u-v-Koordinatensystem benötigt werden, werden zunächst zwei Vektoren u und v in Richtung der u- bzw. v-Achse bestimmt, die dann zu den Einheitsvektoren ue und ve des Bildebenen-Koordinatensystems normiert werden:
Der Normalenvektor n wird durch Division durch seinen Betrag zum Normalen-Einheitsvektor
![]()
Der "Up vector" uv kann als Summe des Vektors v und eines Vektors k ve (mit zunächst noch unbestimmten Faktor k) aufgeschrieben werden:
uv = v + k ne .
Multiplikation dieser Beziehung mit ne führt wegen ne·v = 0 (Vektoren stehen senkrecht aufeinander) und mit ne·ne = 1 auf
k = ne · uv ,
was in den Ansatz für uv eingesetzt werden kann. Aus dem daraus berechneten Vektor
v = uv − (ne · uv) · ne
entsteht schließlich der Einheitsvektor in Richtung der v-Achse:
![]()
Der Einheitsvektor in Richtung der u-Achse kann nun einfach aus dem Vektorprodukt
ue = ne x ve
berechnet werden.
Mit den (gesuchten) Koordinaten u und v des Punktes P' kann der Vektor p' zu diesem Punkt formal aufgeschrieben werden als
p' = r0 + u ue + v ve .
Da der Endpunkt des Vektors c ("Eye point") und die Punkte P' und P auf einer Geraden liegen (Sehstrahl), können sich die beiden Differenzvektoren (p' − c) und (p − c) nur um einen (zunächst ebenfalls noch unbekannten) Faktor unterscheiden:
(p' − c) λ = (p − c) .
Aus den beiden letzten Beziehungen wird der Vektor p' eliminiert (die Koordinaten des Punktes P' im dreidimensionalen Koordinatensystem sind ohnehin nicht interessant), und es verbleibt mit
(r0 + u ue + v ve − c) λ = p − c
eine Vektorgleichung für die drei Unbekannten u, v und λ. Die Vektoren werden durch ihre Komponenten dargestellt:
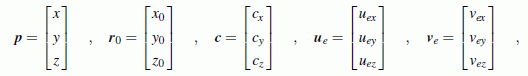
für die Produkte der unbekannten Koordinaten u und v mit λ werden neue Unbekannte eingeführt:
u = u λ , v = v λ .
Dann kann die oben angegebene Vektorgleichung als lineares Gleichungssystem formuliert werden. Die Lösung von
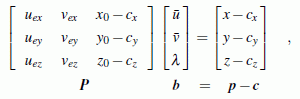
liefert den Vektor der (ebenen) homogenen Koordinaten des Punktes P' im Koordinatensystem der Bildebene:
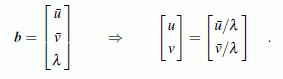
Die Projektion versagt für λ = 0, was folgende Gründe haben kann:
- Der zu projizierende Punkt P ist identisch mit dem "Eye point" (p = c), oder
- der Sehstrahl und der Normalenvektor der Projektionsebene stehen senkrecht aufeinander.
In beiden Fällen ist natürlich auch keine sinnvolle Projektion möglich. Formal liefert die Projektion auch Bildkoordinaten u und v, wenn der Körperpunkt P hinter dem "Eye point" liegt. Diese Fälle, die sich durch ein negatives λ äußern, sollten aussortiert werden.
Im Gegensatz zur Parallelprojektion gibt es bei der Zentralprojektion Kombinationen der Parameter, für die keine sinnvolle Darstellung möglich ist. Dies ist begründet in der Besonderheit, dass sich der Betrachter (mit seinem "Eye point") auch im Inneren des darzustellenden Objekts befinden kann, was natürlich auch eine besondere Stärke der Zentralprojektion ist.
Weil für diese Situation besondere Maßnahmen erforderlich sind, gibt es dafür eine spezielle Seite "Spezielle Probleme der Zentralprojektion, der Kamera-Winkel", die man aber erst besuchen sollte, nachdem man sich mit den allgemeinen Problemen der 3D-Darstellung vertraut gemacht hat.
Weiterlesen
- Empfehlung zum Weiterlesen: Auf der Seite "Mathematk der Parallelprojektion" werden die Formeln der Theorie der Parallelprojektion zusammengestellt.
- Wer kein Interesse an theoretischen Grundlagen hat (oder wem die Theorie der Zentralprojektion ausreicht), kann auch sofort zur Seite "Definition der Projektionen in CanvasGI" wechseln.
- "Reine Praktiker" wechseln vielleicht sogar direkt zur Seite "Projektionen, Beispielprogramm Projektion 1". Man kann ja dann, wenn man etwas nicht versteht, bei Bedarf zurückspringen.

