"Drahtmodelle" zeichnen
Nebenstehend sieht man die Zeichnung eines "3D-Drahtmodells", das mit zwei Arrays definiert wird, wie es auf der Seite "Einfache 3D-Modelle" beschrieben wird. Man kann durch Anklicken eines Buttos in der unteren Reihe zwischen vier verschiedenen Modellen wählen.
Die Zeichnung entsteht in folgenden Schritten:
- Im Body-Teil der HTML-Datei wird der Canvas-Bereich mit der id="canvas"
erzeugt, die Zeichenaktion wird gestartet durch eine Anweisung im Body-Tag:
<body onLoad="init();">
- In der JavaScript-Funktion init wird das cavasGI-Objekt erzeugt und einer global vereinbarten Variablen gi zugewiesen, damit es in allen anderen Funktionen verfügbar ist.
- Das aktuelle Modell wird durch zwei global vereinbarte Arrays xyz und edges repräsentiert. Beim Start der Seite soll der Würfel sichtbar sein, deshalb werden diesen beiden Arrays die Arrays cubexyz und cubeedges (befinden sich in der eingebundenen Datei drahtmodelle.js) zugewiesen.
- Die 3D-Koordinaten ("World coordinates") der Modelle werden vor der Zeichenaktion mit der gültigen Projektion auf ebene "User coordinates" umgerechnet. Um mit der Definition der "User coordinates" für die Zeichenfläche einen "passenden Bereich" vorzusehen, gibt es die Hilfs-Funktion ptlimits, der ein 3D-Koordinaten-Array übergeben wird. Die Funktion liefert die Extremwerte der 2D-Koordinaten ab, die bei der Projektion entstehen. Dies wird hier genutzt, um mit setusercoordsi einen passenden Bereich (bei einem Rand von 20%) einzustellen (die beiden hellblauen Zeilen im folgenden Listing).
- Schließlich wird die Funktion draw aufgerufen, die das Modell zeichnet. So sieht die komplette Funktion init aus:
function init () {
gi = new canvasGI ("canvas") ; // Ein "CanvasGI-Objekt" wird erzeugt
xyz = cubexyz ; // Beim Start soll der Wuerfel ...
edges = cubeedges ; // erscheinen
var limits = gi.ptlimits (xyz) ; // ... ermittelt Grenzen der "User coordinates"
gi.setusercoordsi (limits.xumin , limits.yumin , limits.xumax , limits.yumax , 20) ;
draw () ;
}
In der Funktion draw wird das Modell gezeichnet. Hier werden Funktionen verwendet, die die Zeichenaktionen in einem "Path" sammeln, um das komplette Model dann über stroke und fill zu zeichnen:
function draw () {
var k1 , k2 ;
gi.clearcanvas ("silver" , "black") ; // ... fuellt Canvas-Bereich mit Hintergrundfarbe
// ("silver") und zeichnet schwarzen Rahmen
gi.beginpath () ; // ... startet einen "Path"
for (var i = 0 ; i < edges.length ; i++) {
k1 = edges[i][0] ;
k2 = edges[i][1] ;
gi.wtline (xyz[k1][0] , xyz[k1][1] , xyz[k1][2] , xyz[k2][0] , xyz[k2][1] , xyz[k2][2]) ;
}
for (var i = 0 ; i < xyz.length ; i++) {
gi.wtmarker (xyz[i][0] , xyz[i][1] , xyz[i][2] , gi.MKCIRCLE , 2) ;
}
gi.fillstyle ("red") ;
gi.strokestyle ("black") ;
gi.stroke () ; // ... zeichnet den definierten "Path"
gi.fill () ; // ... fuellt die Marker
}
- Alle CanvasGI-Funktionen, deren Namen mit "wt..." beginnen (hier wtline und wtmarker), erwarten "World coordinates" (Koordinatentripel, die sich auf ein kartesisches 3D-Koordinatensystem beziehen). Diese werden vor der Zeichenaktion der jeweils gültigen Transformation unterworfen, was beim Start der Seite noch keine Auswirkungen hat, weil noch keine Transformation definiert ist, aber für die nachfolgenden Angebote zur Verschiebung und Rotation werden diese Funktionen hier schon vorsorglich verwendet.
- Die Funktion wtline erwartet die Koordinaten zweier Punkte P1 und P2 in der Reihefolge x1, y1, z1, x2, y2, z2 und verbindet diese Punkte mit einer geraden Linie. Sie ist hier in eine Schleife über alle Kanten des Modells eingebettet.
- Die Funktion
wtmarker (xw , yw , zw , mtype , msize)
zeichnet einen "Marker" (vgl. Seite "Marker zeichnen") an der durch xw, yw, zw vorgegebenen "World coordinates"-Position. Hier wird ein gefüllter Kreis (Markertyp gi.MKCIRCLE) in doppelter Standardgröße (für mksize wird eine 2 vorgegeben) gezeichnet. Die Funktion ist in eine Schleife über alle Knoten des Modells eingebettet.
Bewegen des Modells
Über die Buttons unterhalb der Zeichenfläche werden Änderungen der Transformationsmatrix ausgelöst. Dies ist für die Translationen folgendermaßen programmiert:
<input type="button" value="x+" name="plusx"
style="width:37px; height:27px; font-size:small;" onclick="xplus (1,0,0);" />
<input type="button" value="y+" name="plusx"
style="width:37px; height:27px; font-size:small;" onclick="xplus (0,1,0);" />
<input type="button" value="z+" name="plusx"
style="width:37px; height:27px; font-size:small;" onclick="xplus (0,0,1);" />
<input type="button" value="x-" name="plusx"
style="width:37px; height:27px; font-size:small;" onclick="xplus (-1,0,0);" />
<input type="button" value="y-" name="plusx"
style="width:37px; height:27px; font-size:small;" onclick="xplus (0,-1,0);" />
<input type="button" value="z-" name="plusx"
style="width:37px; height:27px; font-size:small;" onclick="xplus (0,0,-1);" />
function xplus (x , y , z) {
gi.t3translation (x , y , z) ;
draw () ;
}
|
Beim Anklicken eines Buttons der oberen Reihe wird also immer eine Funktion xplus aufgerufen, der die drei Komponenten der Translation übergeben werden. Die Funktion ist nebenstehend zu sehen. Mit gi.t3translation(x,y,z) wird die entsprechende Translation zur vorab gültigen Transformation hinzugefügt. Hier ist es jeweils eine Verschiebung parallel zu einer Koordinatenachse der "World coordinates" um eine Einheit.
Rotation des Modells als Animation
Während die oben beschriebene Translation das Modell nach einigen Bewegungen aus der Zeichenfläche verschwinden lässt, bietet sich die Rotation des Modells dafür an, die Realisierung von Animationen zu demonstrieren. Ausgelöst werden diese durch die Buttons der zweiten Reihe:
<input type="button" value="φx+" name="phiplusx"
style="width:37px; height:27px; font-size:small;" onclick="phiplus (gi.AXIS_X);" />
<input type="button" value="φy+" name="phiplusy"
style="width:37px; height:27px; font-size:small;" onclick="phiplus (gi.AXIS_Y);" />
<input type="button" value="φz+" name="phiplusz"
style="width:37px; height:27px; font-size:small;" onclick="phiplus (gi.AXIS_Z);" />
Beim Anklicken eines Buttons wird also eine Funktion phiplus aufgerufen, der als Parameter die Rotationsachse übergeben wird. Diese Funktion überträgt diesen Parameter auf eine global vereinbarte Variable rotax, damit diese Information auch in anderen Funktionen zugängig ist und startet mit setInterval die Animation:
function phiplus (axis) {
rotax = axis ;
if (anim == 1) { // ... wird eine laufende Rotation ...
window.clearInterval (aktiv) ; // ... gestoppt
}
anim = 1 ;
aktiv = window.setInterval("rotation ()" , dT) ; // ... startet Animation
}
function rotation () {
gi.t3rotation (dPhi , rotax) ;
draw () ;
}
|
Die Programmzeile
aktiv = window.setInterval("rotation()" , dT) ;
sorgt dafür, dass eine Funktion rotation() ab sofort immer wieder im zeitlichen Abstand von dT Millisekunden gestartet wird. Diese kleine Funktion ist nebenstehend zu sehen. Sie bringt bei jedem Aufruf mit gi.t3rotation(dPhi,rotax) eine zusätzliche Rotations-Transformation um den Winkel dPhi um die Achse rotax auf und startet mit der Funktion draw das Löschen der alten Zeichnung und das Zeichnen unter Verwendung der aktualisierten Transformation. Im aktuellen Programm sind für den Zeitschritt dT = 100 Millisekunden und für den Winkelschritt dPhi = Math.PI/36 (5°) global vereinbart.
Beim Aufruf von setInterval wird ein Wert abgeliefert, der zur Identifizierung der Aktion dient (hier in der globalen Variablen aktiv gespeichert) und es gestattet, die Aktion zu beenden. Dafür ist der Button "Rotation stoppen" vorgesehen:
<input type="button" value="Rotation stoppen" name="stoprot"
style="width:120px; height:27px; font-size:small;" onclick="phistopp ();" />
function phistopp () {
anim = 0 ;
window.clearInterval (aktiv) ;
}
|
Die beim Anklicken dieses Buttons aufgerufene Funktion phistopp ist nebenstehend zu sehen. Mit window.clearInterval(aktiv) wird die Animation gestoppt.
Das Beispiel-Programm "Drahtmodelle zeichnen" enthält neben allen hier beschriebenen Bausteinen zusätzlich das Angebot, die Projektion und alle Projektionsparameter zu ändern.
Vor- und Nachteile der Drahtmodelle
Dem Vorteil, Drahtmodelle mit wenig Aufwand (und damit sehr schnell) zeichnen zu können, steht ein gravierender Nachteil gegenüber: Die Bilder enthalten keine Information darüber, welche Kanten vorn bzw. hinten liegen. Schon beim Betrachten des Würfels, der nach dem Seitenstart erscheint, kann es passieren, dass man ihn plötzlich nicht mehr "von oben" sondern "von unten" sieht. Wenn man ihn um die vertikale Achse rotieren lässt, wechselt er sogar manchmal (natürlich nur scheinbar) die Drehrichtung.
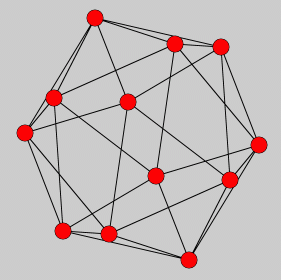
Bei dem nebenstehend dargestellten Ikosaeder (besteht aus 20 gleichseitigen Dreiecken) ist es noch schwieriger zu entscheiden, welche Kanten vorn und welche weiter hinten liegen. Weil die Modell-Definitionen aber die Informationen enthalten, wo sich jedes Element im Raum befindet, kann man sie auch auswerten. Dies wird auf der Seite "Flächenmodelle" demonstriert.
Weiterlesen
Empfehlung zum Weiterlesen: Auf der Seite "Hidden lines", "Edges", "Silhoutte lines", "Lightness" werden die Probleme der realitätsnahen Darstellung von 3D-Objekten diskutiert. Auf den folgenden Seite werden einfache Lösungen demonstriert:

