Aus der Formel für die Bogenlänge einer Kurve, die durch eine Funktion y = y(x) beschrieben wird, entsteht durch Ersetzen der Ableitung entsprechend

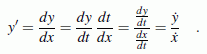
die Formel für die Länge des Bogens einer Funktion, die in Parameterdarstellung gegeben ist. Es ist die zwischen den beiden Punkten, die durch die Parameterwerte ta und tb beschrieben werden, liegende Strecke (in der nebenstehenden Skizze rot gezeichnet):
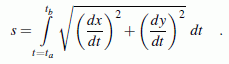
Beispiel
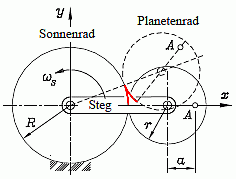
Der Steg eines Planetengetriebes dreht sich mit der konstanten Winkelgeschwindigkeit ωS und treibt ein Planetenrad, das auf dem feststehenden Sonnenrad abrollt. Das Bewegungsgesetz des Punktes A im Abstand a vom Mittelpunkt des Planetenrades kann aus der Bedingung, dass die auf den beiden Rädern abgewälzten Bögen gleich sein müssen (sind in der Skizze rot gezeichnet), in Parameterdarstellung formuliert werden (t ist die Zeit, Zeitzählung beginnt in der Lage, die die Skizze rechts zeigt):
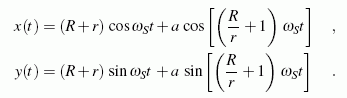
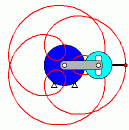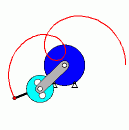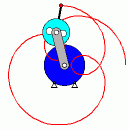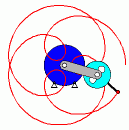
Nebenstehende Animation zeigt ein Beispiel mit den speziellen Abmessungen R/r = 1,5 und a/r = 2 (der zu untersuchende Punkt liegt außerhalb des Planetenrades. Bei diesem Radienverhältnis ergibt sich erst nach 2 Stegumläufen eine geschlossene Bahnkurve des Punktes A. Die Länge dieser (in der Animation rot gezeichneten) Kurve soll für die gewählten Abmessungsverhältnisse mit r = 10 cm berechnet werden.
Die Winkelgeschwindigkeit darf beliebig gewählt werden (für die Berechnung des zurückgelegten Weges kommt es nicht darauf an, wie schnell er durchlaufen wurde). Wenn ωS = 1 gesetzt wird, müssen die Integrationsgrenzen 0 ≤ t ≤ 4π sein, um zwei volle Stegumläufe zu realisieren:
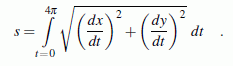
Die Ableitungen der beiden Funktionen x(t) und y(t) nach t können gebildet und in diese Formel eingesetzt werden. Für das entstehende Integral kann nur die numerische Lösung empfohlen werden (dieser Weg wird auf der Seite "Punkt auf Planetenrad" demonstriert). Hier wird der noch bequemere Weg gezeigt, dem Programm "Funktionen analysieren" auch die Bildung der Ableitungen nach t zu übertragen.
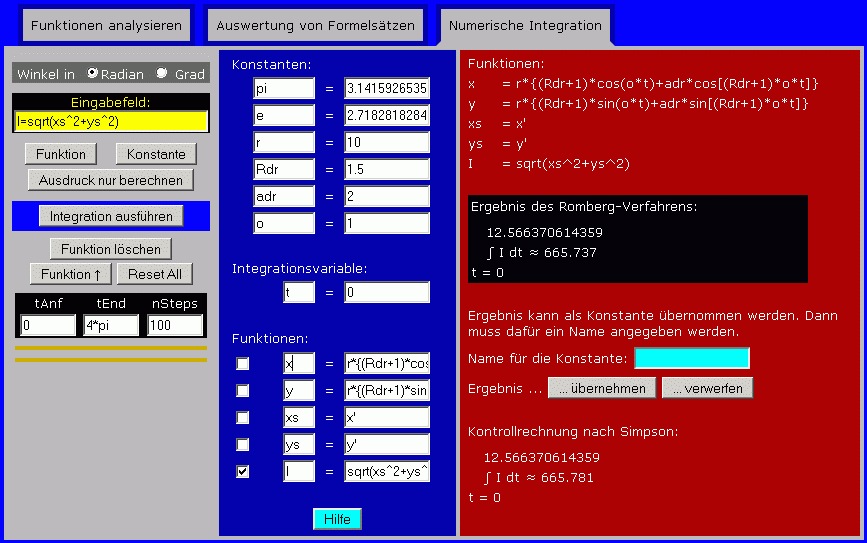
Nach dem Start des Programms und Anklicken des Reiters "Numerische Integration" werden zunächst die Konstanten r, Rdr (steht für "R durch r"), adr und o (für "omega") definiert. Die Integrationsvariable wird auf t umgestellt und die Grenzen werden mit tAnf = 0 bzw. tEnd = 4*pi festgelegt. Nach Eingabe der Funktionen x und y werden als zusätzliche Funktionen xs = x' (Ableitung von x nach der Integrationsvariablen) und ys = y' definiert, schließlich der Integrand I. Dann kann auf "Integration ausführen" geklickt werden, und der Bildschirm zeigt alle Eingabewerte und die Ergebnisse der numerischen Integration: