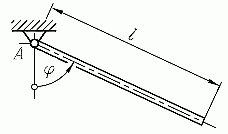
 Ein dünner Stab der
Länge l mit konstantem
Querschnitt ist an einem Ende reibungsfrei gelagert. Er
wird aus der vertikalen Lage um den Winkel
φ0 ausgelenkt
und ohne Anfangsgeschwindigkeit freigegeben (Luftwiderstand kann
vernachlässigt werden).
Ein dünner Stab der
Länge l mit konstantem
Querschnitt ist an einem Ende reibungsfrei gelagert. Er
wird aus der vertikalen Lage um den Winkel
φ0 ausgelenkt
und ohne Anfangsgeschwindigkeit freigegeben (Luftwiderstand kann
vernachlässigt werden).
Gegeben: Erdbeschleunigung g = 9,81 m/s2 , φ0 = 3π/4.
Es soll die Abhängigheit der für eine volle Schwingung benötigten Zeit T (Schwingungsdauer, "einmal hin und zurück") von der Pendellänge l als Funktion T(l) für den Bereich 1 cm ≤ l ≤ 1 m ermittelt werden.
Das Problem besteht darin, dass selbst das Bewegungsgesetz φ(t) nicht mit einem analytischen Ausdruck formuliert werden kann. Im Kapitel "Kinetik starrer Körper" des Lehrbuchs "Dankert/Dankert: Technische Mechanik" wird gezeigt, dass für das Bewegungsgesetz das folgende Anfangswertproblem gilt:
Dieses nichtlineare Anfangswertproblem kann nur numerisch integriert werden. Man findet die Lösung dieses Problems als Beispiel 1 für das Programm "Anfangswertproblem" (unter "TM-interaktiv"), außerdem ist hier die Lösung mit Matlab beschrieben. Mit den dort demonstrierten Lösungen ist die Berechnung nur jeweils eines Punktes der Funktion T(l) möglich.
Lösung mit Matlab
Das oben angegebene Anfangswertproblem wird mit dem Matlab-Standardsolver ode45 gelöst. Es genügt, die Zeit für eine halbe Schwingung (φ = 3π/4 ... −3π/4) zu ermitteln, die Schwingungsdauer T ist das Doppelte dieses Wertes. Dies wird mit der Matlab-Event-Strategie realisiert, als "Ereignis" wird "Winkelgeschwindigkeit gleich Null" (am Umkehrpunkt der Bewegung) definiert. Dann ist ein Wert Ti(li) bekannt. Um diesen Algorithmus wird eine Schleife gelegt, die die Berechnung für alle gewünschten li-Werte durchführt.
Das nachfolgend gelistete Matlab-Script realisiert diese Rechnung:
- Die weißen Zeilen sind der Kern des Scripts. In einer Schleife, in der die Pendellänge verändert wird, wird das Anfangswertproblem gelöst. Jede Rechnung endet beim Eintreten des definierten Ereignisses, und die Zeit, die jeweils für die Schwingung benötigt wurde, wird in einem Vektor gespeichert, in einem anderen Vektor die zugehörige Pendellänge.
- Die hellblauen Zeilen zeigen einerseits, dass über die Optionen angekündigt wird, dass während der Rechnung auf ein Ereignis zu achten ist (ein Ereignis ist in Matlab immer ein Nulldurchgang). Dieses wird in der Funktion "Ereignis" definiert: Die Winkelgeschwindigkeit bestimmt das Eintreten des Ereignisses (value), die Rechnung soll beim Eintreten des Ereignisses abgebrochen werden (isterminal), und zwar unabhängig davon, in welcher Richtung der Nulldurchgang erfolgt (direction).
- Die beiden Anweisungen nach Abarbeitung der Schleife zur Berechnung der Ti(li)-Werte dienen zur grafischen Darstellung der Funktion und zur Ausgabe einer Wertetabelle in das Command Window.
global pl g
g = 9.81 ;
plbereich = [0.01 1] ;
nsteps = 30 ;
plstep = (plbereich(2) - plbereich(1))/nsteps ;
plen = zeros (nsteps+1 , 1) ;
tend = zeros (nsteps+1 , 1) ;
phi0 = [3*pi/4 ; 0] ; % Anfangswerte
tspan = [0 1000] ; % Zeitintervall (groß genug)
% Optionen für Integration des Anfangswertproblems:
options = odeset ('MaxStep' , 0.01 , 'Events' , @Ereignis) ;
pl = plbereich(1) ;
for i=1:nsteps+1
[t xv te xve ereig] = ode45 (@BewDglPendel , tspan , phi0 , options) ;
plen(i) = pl ;
tend(i) = t(end) * 2 ; % Zeit für eine volle Schwingung
pl = pl + plstep ;
end
plot (plen , tend) , grid on , title ('pl-T-Diagramm:')
[plen tend] % ... schreibt Wertetabelle in das Command Window
% ===================================================================
function [value,isterminal,direction] = Ereignis (t,xvt)
global pl g
omega = xvt(2) ;
value(1) = omega ; % Ereignis 1: "Winkelgeschwindigkeit Null"
isterminal(1) = 1 ; % Abbruch, ...
direction(1) = 0 ; % ... in jedem Fall
% ===================================================================
% Funktion, die die "rechte Seite" des Dgl.-Systems definiert:
function xvp = BewDglPendel (t , xv)
global pl g % ... sind in oben definiert.
phi = xv(1) ; % Input-Werte kommen in ...
omega = xv(2) ; % ... einem Vektor an.
phip = omega ; % Die beiden Differenzialgleichungen
omegap = -1.5*g/pl*sin(phi) ; % werden ausgewertet, ...
xvp = [phip ; omegap] ; % ... die Ergebnisse werden im Vektor xvp abgeliefert.
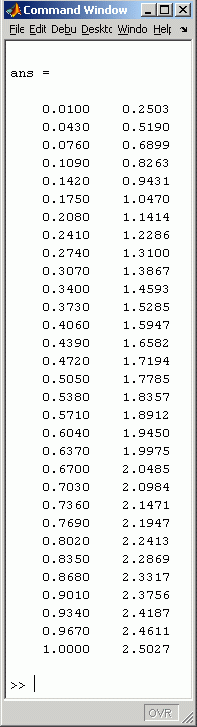 Nebenstehend sieht man die Wertetabelle
Ti(li),
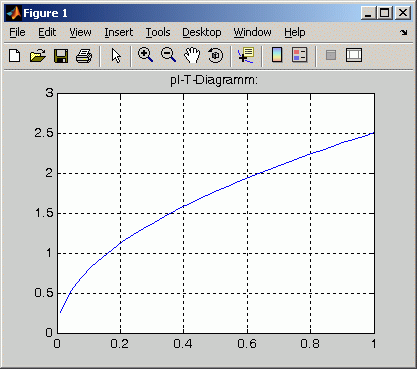
nachfolgend die grafische Darstellung der Funktion
T(l):
Nebenstehend sieht man die Wertetabelle
Ti(li),
nachfolgend die grafische Darstellung der Funktion
T(l):
Das oben gelistete Matlab-Script steht zum Download zur Verfügung.

