Gauß-Jordan-Verfahren
Die Idee des Gaußschen Algorithmus, nacheinander jede Gleichung als Eliminationsgleichung zu benutzen, um in allen nachfolgenden Gleichungen Nullen unterhalb des Hauptdiagonalelements zu erzeugen, führt auf das so genannte gestaffelte System. Durch
Rückwärtseinsetzen
Gestaffeltes System
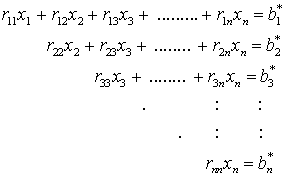 (beginnend mit der letzten Gleichung) können dann nacheinander alle Unbekannten berechnet werden.
(beginnend mit der letzten Gleichung) können dann nacheinander alle Unbekannten berechnet werden.
Eine geringfügige Modifikation erspart das Rückwärtseinsetzen: Wenn der Eliminationsprozess nicht nur auf die nachfolgenden, sondern auf alle Gleichungen mit Ausnahme der Eliminationsgleichung ausgedehnt wird, bleibt in jeder Gleichung nur eine Unbekannte. Wenn diese Gleichung noch durch den Koeffizienten der verbliebenen Unbekannten dividiert wird, ist die Lösung des linearen Gleichungssystems erreicht.
Diese Gauß-Jordan-Verfahren genannte Strategie soll an dem gleichen kleinen Beispiel, das für den Gauß-Algorithmus als Einstiegs-Beispiel diente, demonstriert werden.
Das lineare Gleichungssystem
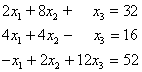
wird schrittweise nach dem Gauß-Jordan-Algorithmus gelöst.
1. Eliminationsschritt:
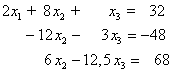 Gleichung 1 bleibt unverändert.
Gleichung 1 bleibt unverändert.- Gleichung 1 wird mit 2 multipliziert und von der 2. Gleichung subtrahiert (die Unbekannte x1 verschwindet aus der 2. Gleichung ).
- Gleichung 1 wird mit -0,5 multipliziert und von der 3. Gleichung subtrahiert (die Unbekannte x1 verschwindet aus der 3. Gleichung).
2. Eliminationsschritt:
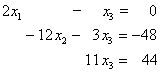 Die Gleichung 2 bleibt unverändert.
Die Gleichung 2 bleibt unverändert.- Die Gleichung 2 wird mit -8/12 multipliziert und von der 1. Gleichung subtrahiert (die Unbekannte x2 verschwindet aus der 1. Gleichung).
- Die Gleichung 2 wird mit -0,5 multipliziert und von der 3. Gleichung subtrahiert (die Unbekannte x2 verschwindet aus der 3. Gleichung).
3. Eliminationsschritt:
- Die Gleichung 3 bleibt unverändert.
- Die Gleichung 3 wird mit -1/11 multipliziert und von der 1. Gleichung subtrahiert (die Unbekannte x3 verschwindet aus der 1. Gleichung).
- Die Gleichung 3 wird mit -3/11 multipliziert und von der 2. Gleichung subtrahiert (die Unbekannte x3 verschwindet aus der 2. Gleichung).
- Das Gleichungssystem hat nach diesem 3. Eliminationsschritt folgendes Aussehen:

In jeder Gleichung ist nur eine Unbekannte verblieben. Nach Division durch den jeweiligen Koeffizienten ergibt sich die Lösung x1 = 4/2 = 2 ; x2 = -36/(-12) = 3 ; x3 = 44/11 = 4 .
Zeilentausch, Singularität, Pivotisierung, Effektivität
Wenn auf der Hauptdiagonalen ein Null-Element entsteht (durch dieses Element muss dividiert werden), ist ein Zeilentausch erforderlich. Noch besser ist die Strategie der Pivotisierung, die gegebenenfalls auch die Singularität der Koeffizientenmatrix anzeigt. Dafür gelten die gleichen Aussagen wie für den klassischen Gauß-Algorithmus.
Die besonders elegante Strategie des Gauß-Jordan-Algorithmus erfordert allerdings für die Lösung linearer Gleichungssysteme mehr Operationen (etwa die 1,5-fache Anzahl an Multiplikationen) als der klassische Gauß-Algorithmus (mit Triangularisierung und Rückwärtseinsetzen), ist also für diese Aufgabe nicht konkurrenzfähig.
Matrixinversion
Der für die Lösung linearer Gleichungssysteme nicht konkurrenzfähige Gauß-Jordan-Algorithmus ist für die Matrixinversion das etwas einfachere Verfahren mit etwa gleichem Aufwand wie für den klassischen Gauß-Algorithmus oder den verketteten Algorithmus für diese Aufgabe. Die Idee für alle diese Verfahren ist, ein lineares Gleichungssystem mit n Gleichungen mit mehreren rechten Seiten zu lösen, und zwar n Spalten, die eine Einheitsmatrix bilden.
Eine Matrizengleichung der Form
![]()
mit der Einheitsmatrix E als rechter Seite hat als Lösung X natürlich die Inverse von A, weil
gilt. Nach dem oben beschriebenen und am Beispiel demonstrierten Gauß-Jordan-Algortihmus, der die Matrix A zur Einheitsmatrix macht, ist das Vorgehen für das Berechnen der Inversen der Matrix A klar:
Man muss an einer Einheitsmatrix die gleichen Operationen vornehmen, die die Matrix A zur Einheitsmatrix machen, und die Einheitsmatrix wird zur Inversen von A.
Matrixinversion, einfaches Beispiel
Für die Matrix A des oben gelösten linearen Gleichungssystems soll die Inverse berechnet werden. Es ist also die Matrizengleichung
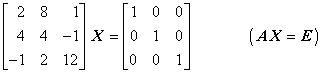
zu lösen. Die einzelnen Gauß-Jordan-Schritte entsprechen denen, die oben für die Lösung des Gleichungssystem ausgeführt wurden.
1. Eliminationsschritt:
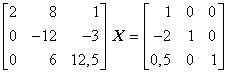 Zeile 1 bleibt unverändert.
Zeile 1 bleibt unverändert.- Zeile 1 wird mit 2 multipliziert und von der 2. Gleichung subtrahiert (das Element a21 in der 2. Zeile wird Null ).
- Zeile 1 wird mit -1/2 multipliziert und von der 3. Gleichung subtrahiert (das Element a13 in der 3. Zeile wird Null ).
2. Eliminationsschritt:
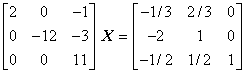 Zeile 2 bleibt unverändert.
Zeile 2 bleibt unverändert.- Zeile 2 wird mit -2/3 multipliziert und von der 1. Gleichung subtrahiert (das Element a12 in der 1. Zeile wird Null ).
- Zeile 2 wird mit -1/2 multipliziert und von der 3. Gleichung subtrahiert (das Element a32 in der 3. Zeile wird Null ).
3. Eliminationsschritt:
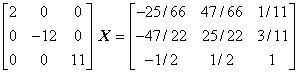 Zeile 3 bleibt unverändert.
Zeile 3 bleibt unverändert.- Zeile 3 wird mit -1/11 multipliziert und von der 1. Gleichung subtrahiert (das Element a13 in der 1. Zeile wird Null ).
- Zeile 3 wird mit -3/11 multipliziert und von der 2. Gleichung subtrahiert (das Element a23 in der 2. Zeile wird Null ).
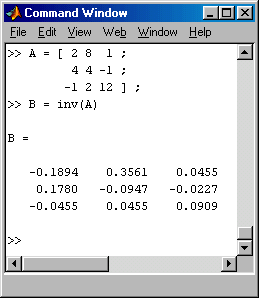 Abschließend wird jede Zeile durch das jeweilige Hauptdiagonalelement diviert. Auf der linken Seite entsteht die Einheitsmatrix, auf der rechten Seite A−1, die Inverse von A:
Abschließend wird jede Zeile durch das jeweilige Hauptdiagonalelement diviert. Auf der linken Seite entsteht die Einheitsmatrix, auf der rechten Seite A−1, die Inverse von A:
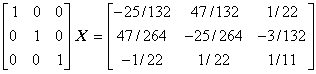
Der Bildschirm-Schnappschuss rechts zeigt die Kontrollrechnung mit der inv-Function von Matlab.
Zeilentausch, Singularität, Pivotisierung
- Zeilentauschoperationen können wie beim klassischen Gauß-Algorithmus erforderlich sein, wenn ansonsten eine Division durch Null auszuführen wäre. Wenn sich keine Zeile mehr finden lässt, die diesen Mangel beheben kann, ist die Matrix A singulär, die Inverse kann nicht berechnet werden.
- Man sollte noch einen Schritt weiter gehen: Um den Einfluss der unvermeidlichen Rundungsfehler zu minimieren, empfiehlt sich eine Pivotisierung in dem Sinne, dass immer mit der Zeile weitergearbeitet wird, die das betragsgrößte Hauptdiagonalelement liefert. Im Gegensatz zur Lösung von Gleichungssystemen müssen hier diese Operationen auch tatsächlich ausgeführt werden (es muss auf der linken Seite eine Einheitsmatrix entstehen mit den Eins-Elementen auf der Hauptdiagonalen), weil sonst in der Inversen die Zeilen falsch angeordnet sind (im oben demonstrierten Beispiel würden im ersten Schritt die 1. Zeile mit der 2. Zeile vertauscht werden (die 4 ist das betragsgrößte Element der 1. Spalte und wird so zum Hauptdiagonalelement).

