 Moderne numerische Berechnungsverfahren (wie Finite-Elemente-Methode, Differenzenverfahren, ...) führen auf sehr große lineare Gleichungssysteme mit 10 000 bis mehr als 1 000 000 Unbekannten. Dabei würden sowohl Speicherkapazität als auch die erforderlichen Rechenzeiten für die Lösung nicht mehr akzeptierbare Grenzen überschreiten, wenn nicht vom Speicheralgorithmus und von den Lösungsalgorithmen die spezielle Struktur der jeweiligen Koeffizientenmatrix des Gleichungssystems ausgenutzt würde (man bedenke, dass schon die Speicherung einer Matrix mit 100 000 Zeilen und Spalten etwa 1010 Speicherplätze mit je 8 Byte erfordert, also etwa 80 Gigabyte).
Moderne numerische Berechnungsverfahren (wie Finite-Elemente-Methode, Differenzenverfahren, ...) führen auf sehr große lineare Gleichungssysteme mit 10 000 bis mehr als 1 000 000 Unbekannten. Dabei würden sowohl Speicherkapazität als auch die erforderlichen Rechenzeiten für die Lösung nicht mehr akzeptierbare Grenzen überschreiten, wenn nicht vom Speicheralgorithmus und von den Lösungsalgorithmen die spezielle Struktur der jeweiligen Koeffizientenmatrix des Gleichungssystems ausgenutzt würde (man bedenke, dass schon die Speicherung einer Matrix mit 100 000 Zeilen und Spalten etwa 1010 Speicherplätze mit je 8 Byte erfordert, also etwa 80 Gigabyte).
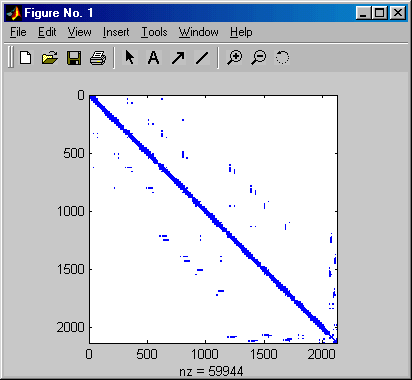
Die Koeffizientenmatrizen, die bei den genannten Diskretisierungsverfahren entstehen, sind in der Regel nur recht dünn mit von Null verschiedenen Elementen besetzt (so genannte "Sparse matrices") Das nebenstehende Bild zeigt das typische "Belegungsmuster" einer Koeffizientenmatrix einer Finite-Elemente-Rechnung (erzeugt mit der spy-function von Matlab mit dem unten vorgestellten kleinen Programm, von 4536900 Matrixelementen sind in diesem Fall nur nz = 59944 Elemente von Null verschieden, also nur etwas mehr als 1%) .
Zwei grundsätzlich unterschiedliche Varianten der Speicherung solcher Matrizen bieten sich an (für eine etwas ausführlichere Beschreibung siehe "Band, Skyline, Sparse und Voll"):
- Weil die von Null verschiedenen Elemente häufig entweder automatisch oder aber durch geeignete Maßnahmen in der Nähe der Hauptdiagnonalen liegen, wird nur dieses "Band" gespeichert (Hauptdiagonale und die entsprechenden Nebendiagonalen), siehe: Gleichungssysteme mit dünn besetzten Matrizen. Eine noch effektivere Variante dieser Speicherstrategie ist die so genannte "Skyline-Speicherung". Diese Speicher-Varianten bieten sich vorwiegend für die Lösung des Gleichungssystem mit direkten Verfahren an.
- Es werden nur die von Null verschiedenen Elemente (und die Information über deren Positionen in der Matrix) gespeichert. Diese Speichervariante ist für iterative Lösungsverfahren zu bevorzugen, allerdings auch für die direkten Verfahren besonders effektiv. Sie ist für zahlreiche Matrix-Operationen (natürlich auch für die Lösung von linearen Gleichungssystemen) in Matlab implementiert.
 Beide Speichervarianten erfordern die Bereitstellung von Lösungsprogrammen, die diese Speicherung verarbeiten und mit möglichst großem Vorteil nutzen .
Beide Speichervarianten erfordern die Bereitstellung von Lösungsprogrammen, die diese Speicherung verarbeiten und mit möglichst großem Vorteil nutzen .
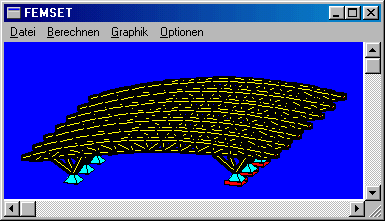
Ein kleines Beispiel soll die Aussagen verdeutlichen (ein weiteres Beispiel findet man hier). Das Finite-Elemente-Modell der nebenstehend zu sehenden Dachkonstruktion (Terminal 4 des Hamburger Flughafens) führt auf ein eher kleines Gleichungssystem mit nur 2130 Gleichungen, an dem sich aber die oben gemachten Aussagen demonstrieren lassen, weil ein Vergleich mit einer Rechnung mit voll besetzter Matrix durchaus noch möglich ist:
Mit Matlab-Femset wird im nachfolgend zu sehenden Matlab-Script das lineare Gleichungssystem erzeugt. Die Koeffizientenmatrix wird einmal in eine voll besetzte quadratische Matrix mit insgesamt 21302 = 4536900 Elementen umgewandelt, zum anderen in eine "Sparse matrix".
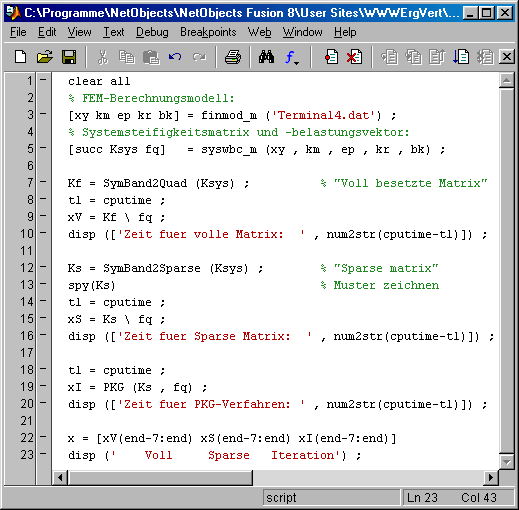 Für beide Varianten wird die Lösung des Gleichungssystems mit dem Matlab-"Backslash-Operator" ausgeführt, die Rechenzeiten werden ermittelt und in das Command Window ausgegeben. Diese sind natürlich vom benutzten PC abhängig, aber die Relationen werden deutlich: Bei voll besetzter Koeffizientenmatrix wird in diesem Fall etwa die 70-fache Zeit benötigt. Da die Rechenzeit bei voll besetzter Matrix proportional zur dritten Potenz der Anzahl der Gleichungen ist, kann man abschätzen, wie schnell eine Erhöhung der Gleichungsanzahl zu nicht mehr akzeptablen Rechenzeiten führen würde.
Für beide Varianten wird die Lösung des Gleichungssystems mit dem Matlab-"Backslash-Operator" ausgeführt, die Rechenzeiten werden ermittelt und in das Command Window ausgegeben. Diese sind natürlich vom benutzten PC abhängig, aber die Relationen werden deutlich: Bei voll besetzter Koeffizientenmatrix wird in diesem Fall etwa die 70-fache Zeit benötigt. Da die Rechenzeit bei voll besetzter Matrix proportional zur dritten Potenz der Anzahl der Gleichungen ist, kann man abschätzen, wie schnell eine Erhöhung der Gleichungsanzahl zu nicht mehr akzeptablen Rechenzeiten führen würde.
Die spy-function in Zeile 13 erzeugt das oben rechts zu sehende "Belegungsmuster" der "Sparse matrix": Nur etwa 1,3% der Matrixelemente sind von Null verschieden.
Schließlich wird die "Sparse matrix"-Variante noch mit einem iterativen Verfahren gelöst. In Zeile 14 wird das "Präkonditionierte Konjugierte-Gradienten-Verfahren" gestartet. Einerseits sind die iterativen Verfahren prädestiniert für Koeffizientenmatrizen mit einer so dünnen Belegung wie in diesem Beispiel, andererseits ist das Problem doch noch nicht groß genug, um die Vorteile der iterativen Verfahren deutlich zu machen. Außerdem ist die Kondition dieses Gleichungssystems nicht so gut, dass bei einem iterativen Verfahren eine besonders schnelle Konvergenz zu erwarten wäre. Deshalb fällt der Zeitvergleich in diesem Fall recht ungünstig aus.
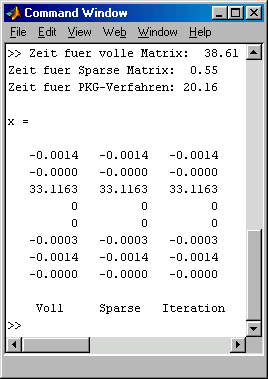 Schließlich wird noch ein kleiner Ausschnitt des Lösungsvektors (die letzten 8 Werte) ausgegeben, der zeigt, dass alle drei Lösungsverfahren (natürlich) das gleiche Ergebnis liefern.
Schließlich wird noch ein kleiner Ausschnitt des Lösungsvektors (die letzten 8 Werte) ausgegeben, der zeigt, dass alle drei Lösungsverfahren (natürlich) das gleiche Ergebnis liefern.
|
Das abgebildete Matlab-Script und die daraus aufgerufenen Functions und DLLs und die Modell-Datei sind zum Download verfügbar: Sparsetest1.m, finmod_m.dll, syswbc_m.dll, SymBand2Quad.m, SymBand2Sparse.m, PKG.m, Terminal4.dat. |

