Allgemeines homogenes Gleichungssystem (rechteckige Koeffizientenmatrix)
Ein lineares Gleichungssystem (m Gleichungen mit n Unbekannten) wird "homogen" genannt, wenn der Vektor der rechten Seite nur Null-Elemente enthält (Nullvektor):
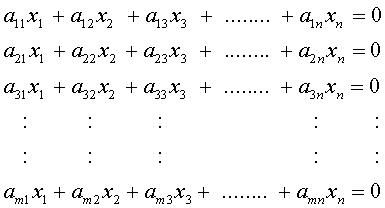 bzw.
bzw. ![]() .
.
Die Lösbarkeitsbedingung für lineare Gleichungssysteme, nach der ein lineares Gleichungssystem dann lösbar ist, wenn der Rang der Koeffizientenmatrix gleich dem Rang der um den Vektor der rechten Seite erweiterten Koeffizientenmatrix ist, ist für homogene Gleichungssysteme immer erfüllt, weil eine Erweiterung einer Matrix mit einer Null-Spalte ihren Rang nicht ändert.
Deshalb gilt für homogene Gleichungssysteme:
- Ein homogenes Gleichungssystem hat immer die so genannte "triviale Lösung"
x1 = x2 = x3 = ... = xn = 0 .
- Ein homogenes Gleichungssystem hat zusätzlich zur trivialen Lösung auch nichttriviale Lösungen, wenn der Rang r(A) der Koeffizientenmatrix kleiner als die Anzahl der Unbekannten n ist. Diese Lösungen sind allerdings nicht eindeutig, denn es können n−r Unbekannte frei gewählt werden.
Anmerkung: Wenn n > m ist (mehr Unbekannte als Gleichungen, "breite" Koeffizientenmatrix), ist die Bedingung r(A) < n immer erfüllt, weil der Rang nicht größer sein kann als der kleinere der beiden Werte m und n. In diesem Fall hat das Gleichungssystem also immer nichttriviale Lösungen.
Praktische Bedeutung kommt diesen Aussagen vornehmlich für den nachfolgend beschriebenen Spezialfall zu.
Homogenes Gleichungssystem mit quadratischer Koeffizientenmatrix
Ein homogenes Gleichungssystem mit quadratischer Koeffizientenmatrix A (n Gleichungen mit n Unbekannten) hat nur die triviale Lösung, wenn die Matrix A regulär ist. Dieser Fall ist im Allgemeinen von geringem Interesse (man beachte den Unterschied zu inhomogenen Gleichungssystemen mit quadratischer Koeffizientenmatrix, bei denen der Fall regulärer Matrix der im Allgemeinen einzige interessierende Fall ist, weil dann das System eine eindeutige Lösung hat).
|
|
Das homogene Gleichungssystem
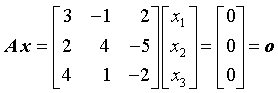
hat eine reguläre Koeffizientenmatrix (auf der Seite "Determinanten n-ter Ordnung" wird gezeigt, dass für die Determinante dieser Matrix det(A) = − 21 gilt). Es hat deshalb nur die triviale Lösung
x1 = x2 = x3 = = 0
(ein beliebiges Lösungsverfahren, z. B. der Gaußsche Algorithmus, würde auch dieses Ergebnis liefern).
Das homogene Gleichungssystem
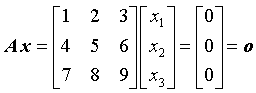
hat dagegen eine singuläre Koeffizientenmatrix (man überzeugt sich leicht, dass det(A) = 0 gilt, denn die dritte Zeile ist gleich der Differenz des Doppelten der zweiten Zeile und der ersten Zeile). Man erhält nach einigen elementaren Umformungen (entsprechend dem Gauß-Algorithmus):
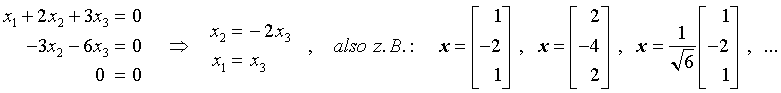
Hier wurde x3 als die beliebig festzulegende Unbekannte gewählt, rechts sieht man eine kleine Auswahl möglicher Lösungen. Der letzte der angegebenen drei Lösungsvektoren ist die normierte Variante des Lösungsvektors (Vektor der Länge 1). Mit der zusätzlichen Forderung "Normierter Lösungsvektor" wird auch für diesen Fall die Lösung eindeutig.
Ist der Defekt der Koeffizientenmatrix größer als 1, dann können mehrere Unbekannte frei gewählt werden. Mit den zusätzlichen Forderungen nach normierten und orthogonalen Lösungsvektoren wird auch in diesen Fällen die Lösungsmenge eindeutig. Der Lösungsraum (Menge aller Lösungen) des homogenen Gleichungssystems wird als "Nullraum" oder "Kern" der Matrix A bezeichnet. Der Satz orthonormierter Lösungsvektoren ist dementsprechend eine "Basis des Nullraums".
 Berechnung der "Nullraum-Basis" mit Matlab
Berechnung der "Nullraum-Basis" mit Matlab
Für die Berechnung der Nullraum-Basis einer Matrix bietet Matlab die Function null an. Dies entspricht (wie oben gezeigt wurde) der Ermittlung der nichttrivialen Lösungen eines homogenen Gleichungssystems (Voraussetzung der Existenz solcher Lösungen bei quadratischer Matrix A ist, dass die Matrix singulär ist).
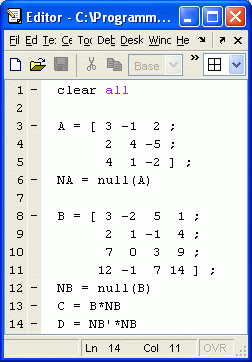 Das nebenstehend links zu sehende kleine Testprogramm NullTest.m demonstriert die Verwendung dieser Function, die auch mit Rechteckmatrizen arbeitet, mit zwei kleinen quadratischen Matrizen. Rechts sind die in das Command Window ausgegebenen Ergebnisse zu sehen.
Das nebenstehend links zu sehende kleine Testprogramm NullTest.m demonstriert die Verwendung dieser Function, die auch mit Rechteckmatrizen arbeitet, mit zwei kleinen quadratischen Matrizen. Rechts sind die in das Command Window ausgegebenen Ergebnisse zu sehen.
Die ab Zeile 3 definierte Matrix A ist die bereits im Beispiel oben verwendete reguläre Matrix, mit der das homogene Gleichungssystem nur die triviale Lösung hat. Dementsprechend kann die Function null kein Ergebnis abliefern ("Empty matrix").
Die ab Zeile 8 definierte Matrix B ist dagegen singulär mit dem Defekt 2. Die Function null liefert zwei Vektoren ab (Ausgabe NB). Mit dem Ergebnis des Produkts in Zeile 13 wird gezeigt, dass beide Vektoren das homogene Gleichungssystem erfüllen (die unvermeidlichen Rundungsfehler führen dazu, dass keine reine Nullmatrix als Ergebnis abgeliefert wird).
Das Produkt in Zeile 14 zeigt, dass die zweispaltige Ergebnismatrix tatsächlich orthonormierte Spalten hat.


