Präkonditionierung (allgemein)
Der Einfluss der Konditionszahl der Koeffizientenmatrix eines linearen Gleichungssystems auf die Lösung wird auf der Seite "Rundungsfehler, Kondition einer Matrix" verdeutlicht. Auf der Seite "Skalierung eines linearen Gleichungssystems" wird eine einfache Möglichkeit beschrieben, die Kondition der Koeffizientenmatrix zu verbessern.
Die Grundidee besteht darin, die Kondition der Koeffizientenmatrix A des linearen Gleichungssystems
![]()
durch Linksmultiplikation mit einer geeigneten Matrix PL und/oder Rechtsmultiplikation mit einer Matrix PR so zu verändern, dass das modifizierte Gleichungssystem z. B. in dem Sinne besser lösbar ist, dass ein iteratives Verfahren schneller konvergiert. Der allgemeine Fall kann so realisiert werden:
![]()
Während die Linksmultiplikation mit PL auf beiden Seiten des Gleichungssystems vorgenommen wird, muss die Rechtsmultiplikation der Matrix A mit PR durch zusätzliche Multiplikation mit deren Inverser kompensiert werden. Es wird also stellvertretend für das Originalsystem das modifizierte System
![]()
mit der (hoffentlich) besser konditionierten Koeffizientenmatrix AP gelöst, dessen Ergebnis anschließend entsprechend
![]()
rücktransformiert werden muss.
Das beschriebene Verfahren ist bei beliebigen Lösungsverfahren für das Gleichungssystem anwendbar. Als "Präkonditionierer" PL bzw. PR kann im einfachsten Fall eine skalierende Diagonalmatrix verwendet werden (für die Lösung mit Eliminationsverfahren in der Regel ausreichend, siehe "Skalierung eines linearen Gleichungssystems"). Für iterative Lösungsverfahren, bei denen Präkonditionierung in der Regel zwingend ist, können raffiniertere Strategien verwendet werden, z. B. die so genannten "unvollständigen Dreieckszerlegungen für schwach besetzte Matrizen" (LU, QR, Cholesky), bei denen in der "klasssischen Variante" nur die Elemente der entstehenden Dreiecksmatrizen berechnet werden, die auf Positionen stehen, die auch in der Ausgangsmatrix von Null verschiedene Elemente hatten (die durch das "Fill-in" entstehenden Elemente werden ignoriert, es gibt jedoch auch Varianten, die von "Diagonalmatrix bis zur komplette Dreieckszerlegung" alle Zwischenstufen ermöglichen, vgl. z. B. Test: Präkonditionierung mit "Incomplete Cholesky").
Die in Matlab angebotenen iterativen Verfahren sind alle auf die Übergabe von "Präkonditionierern" eingerichtet. Auf der Seite "Testrechnungen mit Präkonditionierung mit Matlab" findet man dafür Beispielrechnungen.
Präkonditioniertes Konjugierte-Gradienten-Verfahren
Am Beispiel der Methode der konjugierten Gradienten soll gezeigt werden, dass die oben beschriebene Präkonditionierung in das iterative Lösungsverfahren integriert werden kann, so dass der zusätzlich Aufwand gering ist, wenn man die Konditionierungsmatrizen mit erträglichem Aufwand erzeugt. Weil die Methode der konjugierten Gradienten an die Bedingung geknüpft ist, dass die Koeffizientenmatrix A symmetrisch und positiv definit ist, sollte unbedingt mit einem Präkonditionierer PL gearbeitet werden, der diese Eigenschaften erhält, indem A mit PL von links und zusätzlich mit der Transponierten von PL von rechts multipliziert wird (deshalb wird als Präkonditionierer gern die unvollständige Cholesky-Zerlegung gewählt, weil eine Matrix nach Cholesky in ein Produkt aus Links- und Rechtsdreiecksmatrix zerlegt wird, die zueinander transponiert sind, vgl. auch Test: Präkonditionierung mit "Incomplete Cholesky"). Der oben angegebene allgemeine Fall wird also wie folgt modifiziert:
![]()
Dies kann vorab realisiert werden, wobei eine anschließende Rücktransformation entsprechend
![]()
ausgeführt werden muss. Man kann jedoch die oben angegebenen Beziehungen auch direkt in den Algorithmus der Methode der konjugierten Gradienten einbauen. Dabei zeigt sich, dass das Verfahren nur das Produkt
![]()
benötigt, und man erhält folgenden
Algorithmus des präkonditionierten Konjugierte-Gradienten-Verfahrens:
- Gestartet wird mit einem beliebigen Vektor x0 (dies kann auch ein Nullvektor sein), mit dem ein erster "Residuenvektor" r0 berechnet wird, dessen Produkt mit dem Präkonditionierer P auch als erster "Korrekturvektor" p0 verwendet wird:
![]()
- Jeder Iterationsschritt i folgt folgender Strategie: Der Vektor xi+1 wird durch Korrektur des Vektors xi in die Richtung pi berechnet, wobei die "Schrittlänge des pi-Schrittes" durch einen Faktor λi bestimmt wird:
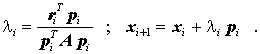
- Als Vorbereitung des folgenden Iterationsschrittes werden ein neuer Residuenvektor ri+1 und ein neuer Korrekturvektor pi+1 berechnet:
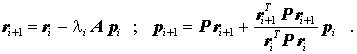
- Es folgt der nächste Integrationsschritt nach den oben angegebenen Formeln. Der Prozess konvergiert, wenn Rundungsfehler keine Rolle spielen, nach n Iterationsschritten (i = 0, 1, 2, ... , n−1). Diese Methode kann also sowohl als Iterationsverfahren als auch als direktes Verfahren gesehen werden, das wie die Eliminationsverfahren das Ergebnis nach einer endlichen Anzahl von Operationen liefert.
Dieser Algorithmus ist in dem Matlab-Script PKG.m realisiert, wobei der Präkonditionierer P in einer gesonderten Function PraeKond (am Ende des Scripts) erzeugt wird. In der zum Download bereitgestellten Version findet man dafür einen "Skalierer" (Diagonalmatrix der reziproken Diagonalelemente von A), also eine besonders einfache Variante, bei Bedarf zu ersetzen durch einen anspruchsvolleren Präkonditionierer.
Auf der Seite "Testrechnungen mit präkonditioniertem KG-Verfahren" wird deutlich, dass selbst die im Matlab-Script PKG.m realisierte besonders einfache Präkonditionierung (Skalierung) gerade bei den Gleichungssystemen, die sich bei Verzicht auf Präkonditionierung der Konvergenz besonders hartnäckig widersetzten (vgl. "Testrechnungen mit iterativen Verfahren (1)" und "Testrechnungen mit iterativen Verfahren (2)"), mit gutem Konvergenzverhalten gelöst werden können. Diese Aussage wird (zumindest für einen Teil der angebotenen iterativen Verfahren) mit den "Testrechnungen mit Präkonditionierung mit Matlab" bestätigt.

