Lineares Gleichungssystem mit n Gleichungen und n Unbekannten
Betrachtet wird eine Beziehung der Form
![]()
mit quadratischer Matrix A, ein Gleichungssystem mit n Gleichungen und n Unbekannten, das - ausführlich aufgeschrieben - so aussieht:
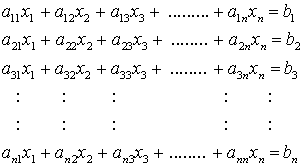
Es soll zunächst vorausgesetzt werden, dass nicht alle bi gleich Null sind (die so genannten homogenen Gleichungssysteme, für die das erfüllt ist, erfordern eine gesonderte Betrachtung) und dass die Matrix A regulär ist (ihre Determinante ist ungleich Null). Dann hat das lineare Gleichungssystem eine eindeutige Lösung.
Idee des Gaußschen Algorithmus
Der Gaußsche Algorithmus verfolgt folgende Strategie:
Durch geeignete Linearkombination der Gleichungen (Multiplikation einer Gleichung mit einem geeigneten Faktor und Subtraktion von einer anderen Gleichung) wird die Koeffizientenmatrix A sukzessive zu einer Rechtsdreiecksmatrix R, dabei ändern sich auch die Werte auf der rechten Seite, aus b wird b* (man sieht leicht ein, dass diese Operationen an der Lösung des Gleichungssystems nichts ändern).
Aus dem so entstehenden "gestaffelten System"
![]()
bzw.
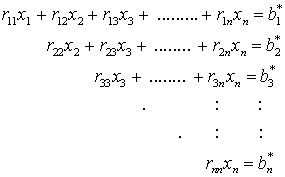
kann dann jeweils genau eine Unbekannte aus einer Gleichung (beginnend mit xn aus der letzten Gleichung) berechnet werden.
Das lineare Gleichungssystem
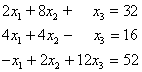
wird schrittweise nach dem Gaußschen Algorithmus gelöst.
1. Eliminationsschritt:
- Gleichung 1 bleibt unverändert.
- Gleichung 1 wird mit l21 = 2 multipliziert und von der 2. Gleichung subtrahiert (die Unbekannte x1 verschwindet aus der 2. Gleichung ).
- Gleichung 1 wird mit l31 = -0,5 multipliziert und von der 3. Gleichung subtrahiert (die Unbekannte x1 verschwindet aus der 3. Gleichung).
- Das Gleichungssystem hat nach diesem 1. Eliminationsschritt folgendes Aussehen:
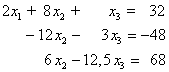
2. Eliminationsschritt:
- Gleichung 1 bleibt unverändert.
- Die veränderte Gleichung 2 bleibt unverändert.
- Die veränderte Gleichung 2 wird mit l32 = -0,5 multipliziert und von der 3. Gleichung subtrahiert (die Unbekannte x2 verschwindet aus der 3. Gleichung).
- Das Gleichungssystem hat nach diesem 2. Eliminationsschritt folgendes Aussehen (gestaffeltes System):
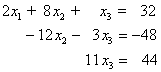
Rückwärtseinsetzen:
- Aus der 3. Gleichung des gestaffelten Systems wird x3 berechnet: x3 = 44/11 = 4 .
- Aus der 2. Gleichung des gestaffelten Systems wird x2 berechnet: x2 = (-48 + 3 · 4)/(-12) = 3 .
- Aus der 1. Gleichung des gestaffelten Systems wird x1 berechnet: x1 = (32 - 8 · 3 - 4)/2 = 2 .
Entsprechend den Eigenschaften von Determinanten (Wert einer Determinante ändert sich nicht, wenn man von einer Zeile ein Vielfaches einer anderen Zeile subtrahiert), hat sich der Wert der Determinante der Matrix A beim Eliminationsprozess nicht geändert (die Determinante der Dreiecksmatrix R hat den gleichen Wert wie die Determinante der Matrix A). Nach den Regeln des Laplaceschen Entwicklungssatzes ist der Wert der Determinante einer Dreiecksmatrix besonders einfach zu berechnen. Man verifiziert leicht, dass dieser sich aus dem Produkt aller Diagonalelemente ergibt, für das Beispiel gilt also:
det (A) = 2 · (-12) · 11 = -264 .
Elimination, Zeilentausch, Singularität, Pivotisierung
Aus dem einfachen Beispiel lassen sich folgende Aussagen über den Gaußschen Algorithmus für ein Gleichungssystem mit n Gleichungen und n Unbekannten ableiten:
- Für die "Triangularisierung" der quadratischen Matrix A mit n Zeilen und n Spalten werden n−1 Eliminationsschritte benötigt.
- Im k-ten Eliminationsschritt werden alle Koeffizienten a*i k mit i = k+1, … ,n (die Elemente unterhalb des k-ten Hauptdiagonalelements) zu Null gemacht.
- Dafür wird die k-te Gleichung (Eliminationszeile) nacheinander mit li k = a*ik/ a*k k multipliziert und von der i-ten Gleichung subtrahiert. Dabei werden auch die b*i auf der rechten Seite verändert.
- Wenn ein Hauptdiagonalelement a*k k, durch das dividiert werden muss, gleich Null ist, wird die Eliminationszeile durch eine der nachfolgenden Zeilen ersetzt (Zeilentausch).
- Wenn sich keine geeignete Zeile für den Zeilentausch finden lässt (alle Elemente unterhalb des Hauptdiagonalelements a*k k haben den Wert Null), dann hat auch die Determinante der Matrix A den Wert Null: Die Koeffizientenmatrix A ist singulär, das lineare Gleichungssystem hat keine eindeutige Lösung.
- Um den unvermeidlichen Einfluss der Rundungsfehler bei der im Allgemeinen sehr großen Zahl von Operationen möglichst gering zu halten, ist es empfehlenswert, vor jedem Eliminationsschritt k einen Zeilentausch so durchzuführen, dass das betragsgrößte aller Elemente unterhalb des k-ten Hauptdiagonalelements und des Hauptdiagonalelements selbst zum Pivotelement gemacht wird (die Zeile mit dem betragsgrößten Element wird zur Eliminationszeile, durch das Pivotelement wird dividiert). Diesen Prozess nennt man Pivotisierung.
- Entsprechend den Eigenschaften von Determinanten (Wert einer Determinante ändert sich nicht, wenn man von einer Zeile ein Vielfaches einer anderen Zeile subtrahiert), ändert sich der absolute Wert der Determinante der Matrix A beim Eliminationsprozess nicht, allerdings führt ein Zeilentausch zu einem Vorzeichenwechsel. Damit kann der Wert der Determinante der Matrix A unter Berücksichtigung der Vorzeichenwechsel beim Zeilentausch aus dem Betrag der Determinante der Rechtsdreiecksmatrix R berechnet werden. Nach dem Laplaceschen Entwicklungssatz gilt für eine Dreiecksmatrix, dass sich der Wert der Determinante aus dem Produkt aller Diagonalelemente errechnet. Also gilt (die ri i sind die Diagonalelemente des gestaffelten Systems):
det (A) = (-1) z · r11 · r22 · r33 · .... · rnn
- Der wesentliche Aufwand des Gaußschen Algorithmus ist der Prozess der Triangularisation der Matrix A. Der Mehraufwand für eine zusätzliche rechte Seite (in der Technischen Mechanik z. B. ein zusätzlicher Lastfall) ist vergleichsweise gering. Um die Lösung für eine zusätzliche rechte Seite zu berechnen, werden ausschließlich die Quotienten li k = a*i k / a*k k benötigt, die man dafür also speichern müsste. Aber genau das ist dann der so genannte verkettete Algorithmus (LR-Zerlegung).
(z ist die Anzahl der Zeilentauschoperationen während des Eliminationsprozesses). Der Gaußsche Algorithmus im Zusammenhang mit dieser Formel ist die effektivste Art der Berechnung von großen Determinanten.

