Die Testrechnungen
Es werden drei FEM-Gleichungssysteme aufgebaut und gelöst, die bei Berechnung mit den von Matlab angebotenen iterativen Lösungsverfahren keine (das 3D-Fachwerk), leichte (das 2D-Rahmentragwerk) bzw. unüberwindliche Probleme (das 3D-Rahmentragwerk) machten (vgl. "Testrechnungen für iterative Verfahren (1)" und "Testrechnungen für iterative Verfahren (2)"). Der für die hier angestellten Betrachtungen uninteressante Algorithmus für den Aufbau des Gleichungssystems wird mit Matlab-Femset ausgeführt.
Die Koeffizientenmatrizen der entstehenden Gleichungssysteme sind symmetrisch und positiv definit (und damit natürlich auch regulär), so dass die notwendigen Voraussetzungen für alle Lösungsverfahren erfüllt sind. Den Matlab-Functions muss eine reguläre Matrix M übergeben werden, als Präkonditionierer wird die Inverse dieser Matrix benutzt. Hier wird jeweils die einfachste Variante der Präkonditionierung (Skalierung, vgl. "Skalierung eines linearen Gleichungssystems") verwendet. Dafür wird eine Diagonalmatrix M an die Matlab-Functions übergeben, die die Diagonalelemente der Koeffizientenmatrix enthält. Die Inverse dieser Diagonalmatrix ist genau die, die auf der Seite "Skalierung eines linearen Gleichungssystems" empfohlen wird, um auf der Hauptdiagonalen Eins-Elemente zu erzeugen (die Inverse einer Diagonalmatrix ist auch eine Diagonalmatrix, die die reziproken Elemente der Originalmatrix enthält).
Dreidimensionales Fachwerk
Die nebenstehend zu sehende Brückenkonstruktion wurde mit dreidimensionalen Fachwerkstäben modelliert. Das FEM-Berechnungsmodell ist in der Datei Fof.dat gespeichert und wird im nachfolgenden Matlab-Script eingelesen. Mit Matlab-Femset wird das lineare Gleichungssystem erzeugt, mit dem die Knotenverschiebungen berechnet werden können. Bei 400 Stäben und 136 Knoten ergibt sich ein Gleichungssystem mit 408 Gleichungen.
Das Matlab-Script PraeKondMatlab1.m formt die Koeffizientenmatrix in eine "Sparse matrix" (Zeile 8) um, bevor das Gleichungssystem zunächst mit dem Matlab-Standard-Solver (Zeile 11) gelöst wird. In Zeile 13 wird die Diagonalmatrix erzeugt, die den 9 Matlab-Functions (Zeilen 15 bis 23) für die Präkonditionierung übergeben wird:
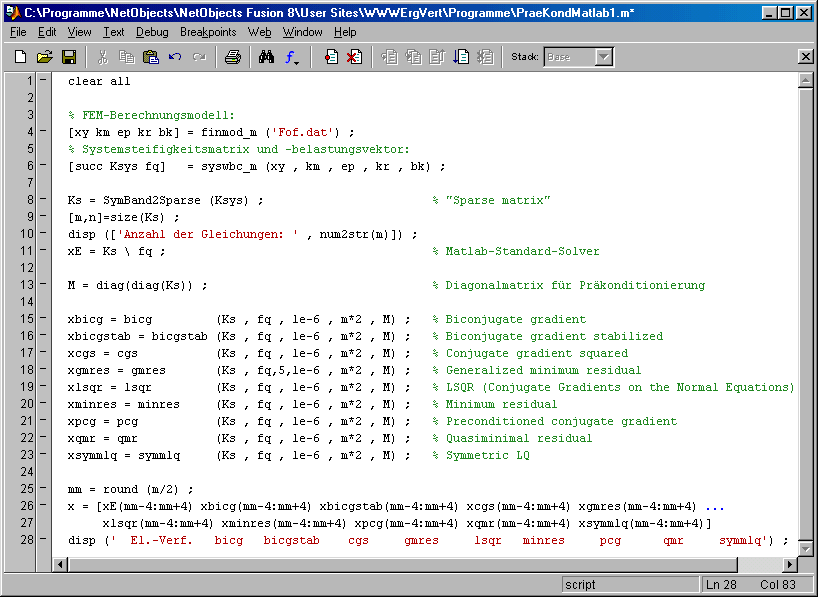
Im Command Window findet man das Ergebnis:
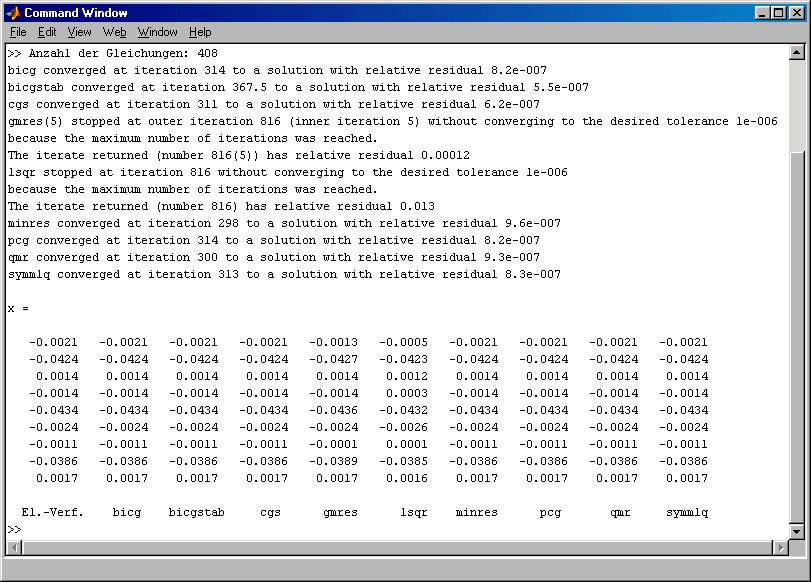
Nur 7 der 9 Verfahren führen zur Konvergenz. Die Functions gmres und lsqr versagten schon bei den Testrechnungen ohne Präkonditionierung, sie werden deshalb für die weiteren Testrechnungen nicht mehr verwendet.
Alle übrigen Verfahren konvergieren im Durchschnitt nach etwas mehr als 300 Iterationsschritten. Dies ist eine Verbesserung um etwa 25% gegenüber der Berechnungen ohne Präkonditionierung, bei denen durchschnittlich etwas mehr als 400 Iterationsschritte benötigt wurden.
Es ist nicht gelungen, mit den Matlab-Functions gmres und lsqr relativ kleine lineare Gleichungssysteme zu lösen, auch Präkonditionierung brachte keine Verbesserung. Auch die Zulassung von wesentlich mehr Iterationsschritten als in den gezeigten Beispielen, in denen der Wert für die maximale Anzahl der Iterationsschritte schon recht großzügig angesetzt wurde, brachte keinen Erfolg.
Die Beispiele mit diesen Functions wurden mit Matlab 6.5 (R13) berechnet. Mit Matlab 7.0 (R14) zeigte sich keine Verbesserung, im Gegenteil: Die Function gmres stürzt unter dieser Version sogar mit einer Fehlermeldung ab.
Zweidimensionales Rahmentragwerk
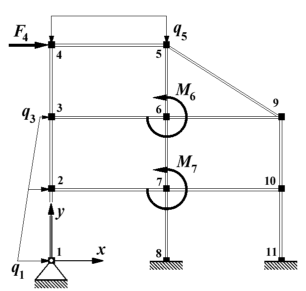
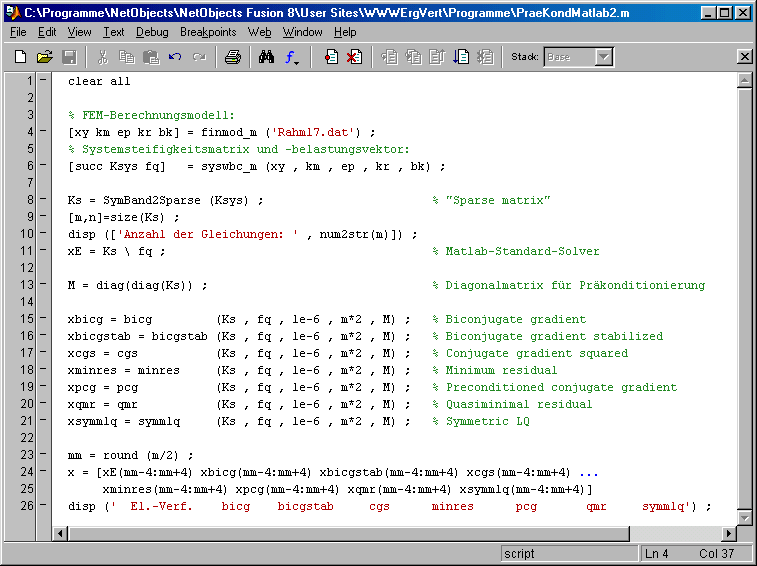
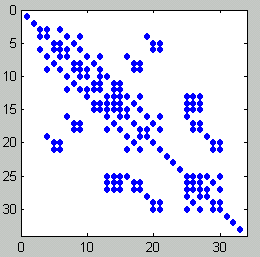Nebenstehend links ist der ebene biege- und dehnsteife Rahmen dargestellt (Beispiel aus dem Kapitel "Verifizieren vom Computerrechnungen"), dessen FEM-Modell in der Datei Rahm17.dat gespeichert ist. Es ist ein sehr kleines Problem, das auf ein Gleichungssystem mit nur 33 Gleichungen führt (rechts das Belegungsmuster der Koeffizientenmatrix mit den von Null verschiedenen Elementen), das allerdings einigen Iterationsverfahren (siehe "Testrechnungen für iterative Verfahren (1)") erhebliche Probleme bereitete. Das nachfolgend zu sehende Matlab-Script PraeKondMatlab2.m entspricht im Aufbau dem oben beschriebenen Script PraeKondMatlab1.m. Auch hier werden von den berechneten Lösungsvektoren jeweils nur einige Elemente ausgegeben:
Im Command Window findet man das Ergebnis:
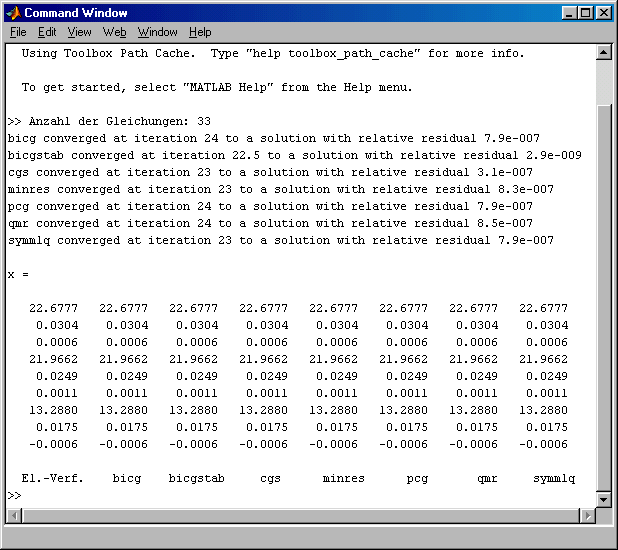
Die Rechnung konvergiert nach 22 bis 24 Iterationsschritten. Dies ist eine deutliche Verbesserung gegenüber den Berechnungen ohne Präkonditionierung, bei denen zwei der hier getesteten Verfahren gar nicht konvergierten (bicgstab und cgs) und die übrigen Verfahren 61 bis 66 Iterationsschritte benötigten.
Dreidimensionales Tragwerk mit biege-, dehn- und torsionssteifen Elementen
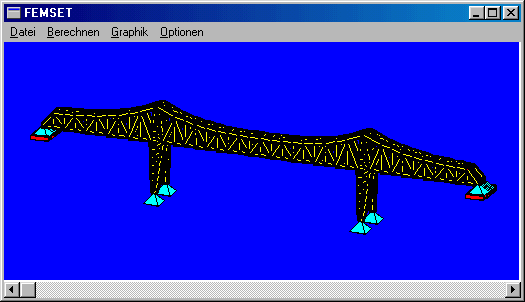Das nebenstehend zu sehende Finite-Elemente-Modell der Brücke über den Nord-Ostsee-Kanal bei Rendsburg besteht aus 1947 Elementen (biege-, dehn- und torsionssteife Träger mit je zwei Knoten), die an 747 Knoten untereinander verbunden sind. Dieses Modell führt auf ein (im Vergleich mit typischen FEM-Modellen eher kleines) Gleichungssystem mit 4482 Unbekannten.
Das FEM-Berechnungsmodell ist in der Datei Rendbrem.dat gespeichert. Es wird das gleiche Matlab-Script PraeKondMatlab2.m verwendet, das zur Berechnung des ebenen Rahmens diente. Darin ist nur (in der Zeile 4) der Name der Datei mit dem Berechnungsmodell von Rahm17.dat in Rendbrem.dat zu ändern.
An diesem Beispiel sind nahezu alle getesteten iterativen Verfahren gescheitert (siehe "Testrechnungen für iterative Verfahren (2)"), nur ein einziges der auch hier getestenen Verfahren (minres) lieferte brauchbare Ergebnisse, allerdings nach völlig inakzeptablen 500000 Iterationsschritten. Obwohl hier nur die einfachste Präkonditionierung (Skalierung) verwendet wird, sieht das Ergebnis ganz anders aus:
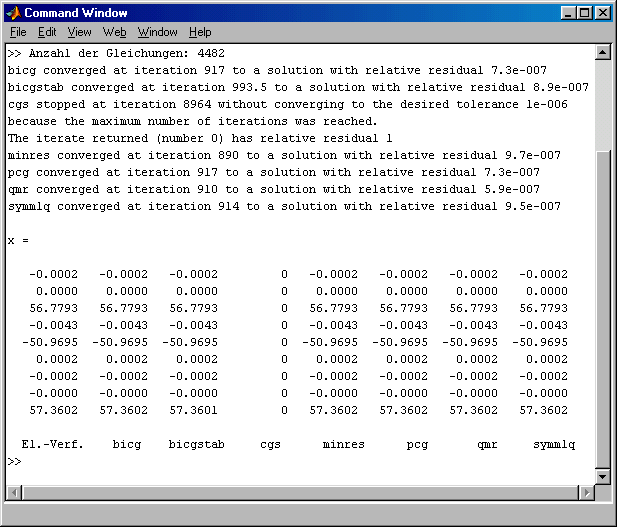
Nur cgs ("Conjugate gradient square") verabschiedet sich mit einer Fehlermeldung. Alle übrigen Verfahren melden Konvergenz nach weniger als 1000 Iterationsschritten.
Fazit der hier durchgeführten Testrechnungen:
- Matlab bietet 9 iterative Verfahren für die Lösung linearer Gleichungssysteme an, von denen zwei (gmres und lsqr) schon bei relativ kleinen Problemen versagten, cgs scheiterte am etwas größeren (aber keineswegs großen) Gleichungssystem. Dass gmres in der Matlab-Version 7.0 mit einer Fehlermeldung abstürzt, verschlechtert die Situation nicht nennenswert, denn auch in der Vorgängerversion konnten kaum brauchbare Ergebnisse erzielt werden.
- Präkonditionierung ist für fast alle Verfahren zwingend, schon mit der einfachsten Variante "Skalierung" wird ein zum Teil drastisch verbessertes Konvergenzverhalten erzielt.
- Alle Matlab-Functions sind für die Übernahme eines Präkonditionierers eingerichtet. Weil die Skalierung überhaupt keinen nennenswerten Mehraufwand erfordert, bleibt die Frage, ob diese nicht die Default-Variante für die iterativen Verfahren sein sollte, wenn kein Präkonditionierer übergeben wird (gegebenenfalls könnte man bei Bedarf diese Art der Präkonditionierung unterdrücken).
- Man lasse sich nicht täuschen vom Namen des pcg-Verfahrens, der für "Preconditioned conjugate gradient" steht. Auch diese Function arbeitet nicht automatisch mit einem Präkonditionierer, sondern nur dann, wenn (wie bei den anderen Verfahren) eine entsprechende Matrix übergeben wird.
Download
Die Matlab-Scripts auf dieser Seite und die von ihnen aufgerufenen Functions, DLLs und Dateien sind zum Download verfügbar:
- Die gezeigten Matlab-Scripts sind als PraeKondMatlab1.m und PraeKondMatlab2.m verfügbar.
- Zusätzlich werden die DLLs finmod_m.dll und syswbc_m.dll und die Matlab-Function SymBand2Sparse.m benötigt. Die FEM-Modelle befinden sich in den Dateien Fof.dat (3D-Fachwerk), Rahm17.dat (2D-Rahmen) und Rendbrem.dat (3D-Tragwerk).
