2 Gleichungen mit 2 Unbekannten, Determinanten

2 lineare Gleichungen mit 2 Unbekannten

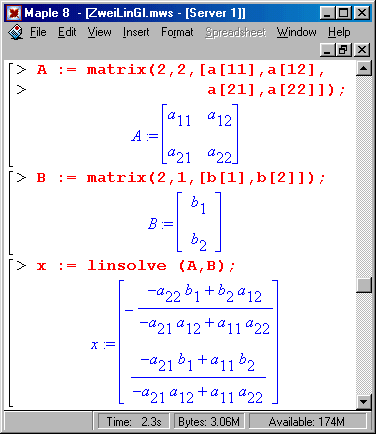
Betrachtet werden die beiden linearen Gleichungen

Erinnerung an die Elementarmathematik: Man ändert nichts an der Richtigkeit von Gleichungen, wenn man

• eine Gleichung auf beiden Seiten mit dem gleichen Faktor multipliziert,
• eine Gleichung zu einer anderen addiert.

Multiplikation der ersten Gleichung mit  -a₂₁/a₁₁ und Addition zur zweiten liefert:

Die Lösung eines solchen Gleichungssystems ist auch möglich mit Mathematik- Programmen, die symbolisch rechnen können. Nachfolgend sieht man die Lösung mit Maple:

(man erkennt, dass die erste Klammer den Wert Null hat). Multiplikation der zweiten Gleichung mit  -a₁₂/a₂₂ und Addition zur ersten liefert:

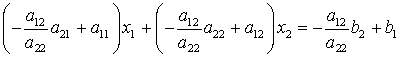
(hier hat die zweite Klammer den Wert Null). Damit ist in jeder Gleichung nur noch eine Unbekannte, und man kann die Lösung des Gleichungssystems nach kurzer Umformung wie folgt aufschreiben.

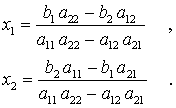
Es fällt auf:

• Beide Formeln haben den gleichen Nenner. Dieser bestimmt die Lösungsmöglichkeit des Gleichungssystems:

 a₁₁a₂₂ - a₁₂a₂₁

darf nicht Null werden (man beachte, dass diese "Lösbarkeitsbedingung" nur mit den Elementen der Koeffizientenmatrix A formuliert wird).

• Auch die beiden Zähler weisen ähnliche Strukturen auf.

Determinanten

Man nennt Ausdrücke, wie sie in Zähler und Nenner der oben entwickelten Lösung des kleinen Gleichungssystems vorkommen, Determinanten und schreibt symbolisch:

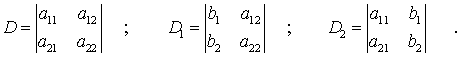
Man beachte den Unterschied:

• Eine Matrix ist ein rechteckiges Schema, in dem Elemente angeordnet sind.
• Eine Determinante ist immer quadratisch, und im Gegensatz zur Matrix ist der Determinante ein Wert zuzuordnen, der sich für die zweireihige Determinante aus folgendem Berechnungsschema ergibt:

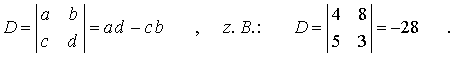
Die Lösung für das oben betrachtete lineare Gleichungssystem mit 2 Unbekannten kann also auch so formuliert werden:

mit der so genannten Koeffizientendeterminante

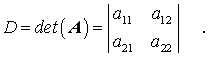
Die Determinanten D₁ und D₂ entstehen aus D, indem die erste bzw. zweite Spalte in D durch die "rechte Seite" b des Gleichungssystems ersetzt werden.

Cramersche Regel

Die mit Determinanten formulierte Lösung des linearen Gleichungssystems kann formal auf die Lösung eines linearen Gleichungssystems mit n Unbekannten übertragen werden, wenn man den Determinanten-Begriff in geeigneter Weise auf  Determinanten n-ter Ordnung erweitert:

Diese so genannte Cramersche Regel ist eine sehr schöne (weil kompakte) Möglichkeit, die Lösung formal aufzuschreiben. Sie ist allerdings wegen des unverhältnismäßig hohen Aufwands schon ab 3 Gleichungen mit 3 Unbekannten nicht konkurrenzfähig mit anderen Lösungsverfahren (z. B. dem Gaußschen Algorithmus).

Die Koeffizientendeterminante  D = det(A)  im Nenner ist der entscheidende Indikator für die Lösbarkeit des linearen Gleichungssystems. Sie muss ungleich Null sein. Man nennt Matrizen, die diese Bedingung erfüllen, regulär, ansonsten singulär.

Eigenschaften von Determinanten

An der Determinante 2. Ordnung lassen sich sehr anschaulich einige wichtige Eigenschaften nachvollziehen, die uneingeschränkt auch für Determinanten höherer Ordnung gelten:

• Die Determinante wechselt das Vorzeichen, wenn man zwei Zeilen (Spalten) vertauscht (weil sich bei der Lösung von Gleichungssystemen natürlich die Ergebnisse nicht ändern, wenn man zwei Gleichungen vertauscht, wechseln neben der Koeffizientendeterminante D auch alle D_i das Vorzeichen, was leicht nachvollziehbar ist).
   
• Eine Determinante hat den Wert Null, wenn eine Zeile (Spalte) nur aus Nullelementen besteht.
   
• Der Wert einer Determinante multipliziert sich mit dem Faktor p, wenn man alle Elemente einer Zeile (Spalte) mit p multipliziert (man beachte den Unterschied zur entsprechenden Regel für Matrizen, bei denen für eine Multiplikation mit einem Skalar gilt, dass alle Elemente der Matrix multipliziert werden müssen).
   
• Der Wert einer Determinante ändert sich nicht, wenn man zu einer Zeile (Spalte) ein Vielfaches einer anderen Zeile (Spalte) addiert.