Matrix-Division mit dem Backslash-Operator
Für Matrizen ist eine Division nicht definiert. In Matlab dagegen gibt es zwei Operatoren, die der Umkehrung der Matrixmultiplikation (im Sinne einer Division) entsprechen:
![]()
Hier soll nur der Backslash-Operator betrachtet werden, der für quadratische Matrix A der Lösung eines linearen Gleichungssystems mit n Gleichungen und n Unbekannten entspricht. In diesem Fall ist der Backslash-Operator nur eine spezielle Schreibweise der Linksmultiplikation mit der Inversen von A (die Realisierung der Operation in Matlab kommt allerdings ganz sicher ohne explizite Bildung der Inversen von A aus):
![]()
Aber auch für beliebige Rechteckmatrizen A liefert Matlab Ergebnisse. Was dabei zu beachten ist, wird nachfolgend besprochen.
Backslash-Operation mit "breiter" Rechteckmatrix
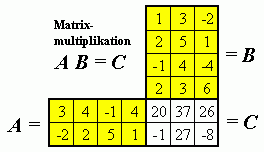
 Links sieht man das
Falksche Schema für die Multiplikation zweier Matrizen
Beispiel für Matrixmultiplikation
Links sieht man das
Falksche Schema für die Multiplikation zweier Matrizen
Beispiel für Matrixmultiplikation
 :
A hat 2 Zeilen und 4 Spalten, B hat 4 Zeilen und 3 Spalten, die sich daraus eindeutig ergebende Ergebnismatrix A·B = C hat nach den Regeln der Matrixmultiplikation 2 Zeilen und 3 Spalten.
:
A hat 2 Zeilen und 4 Spalten, B hat 4 Zeilen und 3 Spalten, die sich daraus eindeutig ergebende Ergebnismatrix A·B = C hat nach den Regeln der Matrixmultiplikation 2 Zeilen und 3 Spalten.
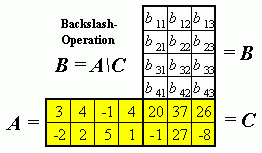
Rechts sieht man das gleiche Schema, in dem aber die Matrizen A und C vorgegeben sind, und die Matrix B soll ermittelt werden. Nach den Regeln der Matrixmultiplikation müssen z. B. die 4 Werte in der ersten Spalte von B nur zwei Bedingungen erfüllen:

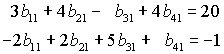
Dies sind 2 Gleichungen für 4 Unbekannte, so dass zwei bi1-Werte frei gewählt werden können, die beiden anderen ergeben sich dann zwangsläufig. Die gleiche Aussage gilt für die beiden anderen Spalten von B.
Fazit: Die "Matrix-Division" mit "breiter" Matrix A (mehr Spalten als Zeilen) ist möglich, das Ergebnis ist aber nicht eindeutig.
Man kann also nicht erwarten, dass sich die bei der Matrixmultiplikation (Schema oben links) verwendete Matrix B bei der "Division" wieder ergibt.
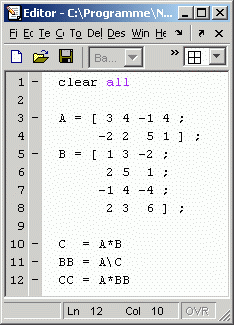
Und genau das liefert die Backslash-Operation in Matlab: Das kleine Script links baut zunächst die beiden Matrizen A und B auf, deren Multiplikation in Zeile 10 das im Falkschen Schema oben links zu sehende Resultat ergibt (siehe "Command window" rechts). Die "Division" (Backslash-Operation) in Zeile 11 liefert aber nicht die Matrix B, sondern eine (zufällige) ganz andere Matrix (hier als BB bezeichnet), die aber durchaus ein richtiges Ergebnis (von unendlich vielen möglichen Ergebnissen) ist, wie die Multiplikation in Zeile 12 beweist.
Backslash-Operation mit "hoher" Rechteckmatrix
Fall a: Es existert eine Matrix B, so dass A·B = C gilt
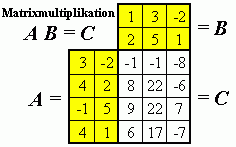
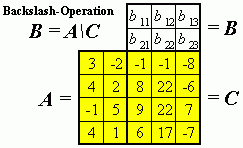 Links sieht man das
Falksche Schema für die Multiplikation zweier Matrizen
Falksche Schema für die Multiplikation zweier Matrizen
Links sieht man das
Falksche Schema für die Multiplikation zweier Matrizen
Falksche Schema für die Multiplikation zweier Matrizen
 :
A hat 4 Zeilen und 2 Spalten, B hat 2 Zeilen und 3 Spalten, die sich daraus eindeutig ergebende Ergebnismatrix A·B = C hat nach den Regeln der Matrixmultiplikation 4 Zeilen und 3 Spalten.
:
A hat 4 Zeilen und 2 Spalten, B hat 2 Zeilen und 3 Spalten, die sich daraus eindeutig ergebende Ergebnismatrix A·B = C hat nach den Regeln der Matrixmultiplikation 4 Zeilen und 3 Spalten.
Rechts sieht man das gleiche Schema, in dem aber die Matrizen A und C vorgegeben sind, und die Matrix B soll ermittelt werden. Nach den Regeln der Matrixmultiplikation müssen z. B. die 2 Werte in der ersten Spalte von B vier Bedingungen erfüllen:
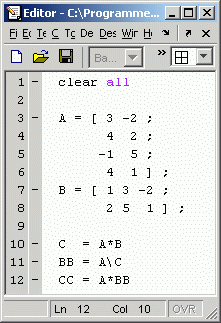
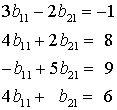
Dies ist ein überbestimmtes Gleichungssystem und in der Regel nicht erfüllbar. In diesem Fall doch, denn die Matrix C wurde ja mit einer Matrix B erzeugt, deren Werte in der ersten Spalte b11 = 1 und b21 = 2 alle 4 Gleichungen erfüllen (man überzeugt sich leicht durch Einsetzen). Die gleiche Aussage gilt für die beiden anderen Spalten von B.
Fazit: Die "Matrix-Division" mit "hoher" Matrix A (mehr Zeilen als Spalten) kann möglich sein, das ist aber eher zufällig.
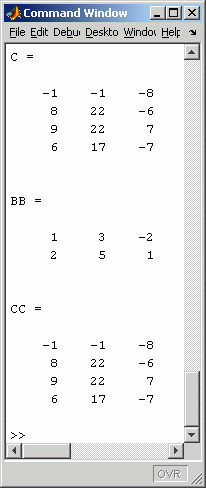
Die Backslash-Operation in Matlab liefert in diesem Fall auch das erwartete Ergebnis: Das kleine Script links baut zunächst die beiden Matrizen A und B auf, deren Multiplikation in Zeile 10 das im Falkschen Schema oben links zu sehende Resultat ergibt (siehe "Command window" rechts). Die "Division" (Backslash-Operation) in Zeile 11 liefert nun genau die erwartete Matrix B (hier als BB bezeichnet).
Fall b: Es existert keine Matrix B, so dass A·B = C gilt
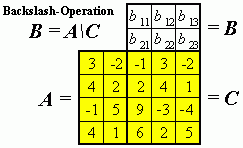 Der als Fall a gezielt konstruierte Fall, dass zu gegebenen Matrizen A und C eine Matrix B existiert, so dass A·B = C gilt, ist natürlich die Ausnahme bei "hoher" Matrix A (mehr Zeilen als Spalten). Rechts sieht man das Falksche Schema, in dem die Matrizen A und C vorgegeben sind, und die Matrix B soll ermittelt werden. Eine solche Matrix existiert aber nicht, denn nach den Regeln der Matrixmultiplikation müssten z. B. die 2 Werte in der ersten Spalte von B die folgenden vier Bedingungen erfüllen:
Der als Fall a gezielt konstruierte Fall, dass zu gegebenen Matrizen A und C eine Matrix B existiert, so dass A·B = C gilt, ist natürlich die Ausnahme bei "hoher" Matrix A (mehr Zeilen als Spalten). Rechts sieht man das Falksche Schema, in dem die Matrizen A und C vorgegeben sind, und die Matrix B soll ermittelt werden. Eine solche Matrix existiert aber nicht, denn nach den Regeln der Matrixmultiplikation müssten z. B. die 2 Werte in der ersten Spalte von B die folgenden vier Bedingungen erfüllen:
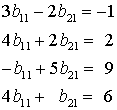
Dieses Gleichungssystem ist widersprüchlich, wie man sich leicht überzeugt: Die beiden ersten Gleichungen (man addiere sie, um das zu überprüfen) können nur erfüllt sein, wenn b11 = 1/7 ist, die beiden letzten Gleichungen (man subtrahiere das 5-fache der vierten von der dritten Gleichung, um das zu überprüfen) können nur erfüllt sein, wenn b11 = 1 ist. Die gleiche Aussage gilt für die beiden anderen Spalten von B.
Fazit: Die "Matrix-Division" mit "hoher" Matrix A (mehr Zeilen als Spalten) ist im Regelfall unmöglich.
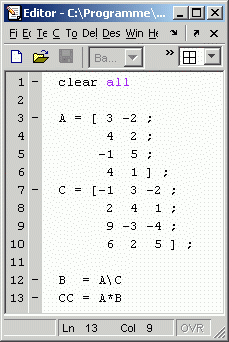
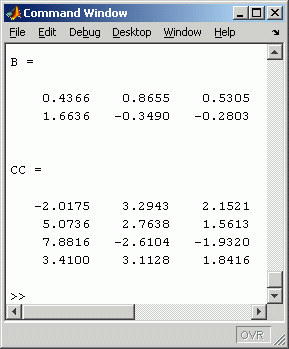 Die Backslash-Operation in Matlab liefert trotzdem ein Ergebnis. Das Gleichungssystem wird nach den Regeln der Ausgleichsrechnung behandelt: Es wird das Ergebnis abgeliefert, das im Sinne des Minimums der Summe der Fehlerquadrate alle Gleichungen "bestmöglich" erfüllt. Für das aufgelistete System für die Berechnung der ersten Spalte der Matrix B ergibt sich in diesem Fall die Lösung: b11 = 0,4366 und b21 = 1,6636. Dieses Wertepaar erfüllt keine der 4 Gleichungen, aber alle 4 in dem genannten Sinne "bestmöglich".
Die Backslash-Operation in Matlab liefert trotzdem ein Ergebnis. Das Gleichungssystem wird nach den Regeln der Ausgleichsrechnung behandelt: Es wird das Ergebnis abgeliefert, das im Sinne des Minimums der Summe der Fehlerquadrate alle Gleichungen "bestmöglich" erfüllt. Für das aufgelistete System für die Berechnung der ersten Spalte der Matrix B ergibt sich in diesem Fall die Lösung: b11 = 0,4366 und b21 = 1,6636. Dieses Wertepaar erfüllt keine der 4 Gleichungen, aber alle 4 in dem genannten Sinne "bestmöglich".
Das kleine Script links demonstriert dies. Es baut zunächst die beiden Matrizen A und C auf. Die "Division" (Backslash-Operation) in Zeile 11 liefert eine Matrix B (Ergebnis rechts im "Command window"), die das Produkt A·B = C nicht erfüllt, wie das Ergebnis der Multiplikation in Zeile 13 beweist. Man erkennt allerdings eine gewisse Tendenz zu den Werten der Matrix C, die in diesem Fall nicht sehr stark ausgeprägt ist, weil die willkürlich aufgeschriebene Matrix C zu sehr starken Widersprüchen im überbestimmten Gleichungssystem führt (bei realistischen Problemen der Ausgleichsrechnung sind die Widersprüche normalerweise eher gering).
"Matrix-Division", Fazit
Die (in der Mathematik nicht definierte) "Matrix-Division", die in Matlab mit Slash und Backslash realisiert wird, liefert dort immer ein Ergebnis. Hinter dem Ergebnis steht auch immer eine sinnvolle Bedeutung. Allerdings muss man schon deshalb genau wissen, was man tut, wenn man diese Operationen anwendet, weil nicht nur verschiedene Algorithmen (in Abhängigkeit von den Eigenschaften der übergebenen Matrizen) arbeiten, sondern auch ganz unterschiedliche Aufgabenstellungen gelöst werden. Man darf stets die Vorstellung haben, dass mit dem Backslash-Operator ein lineares Gleichungssystem
![]()
gelöst wird:
- Bei einer quadratischen Matrix A wird ein lineares Gleichungssystem (n Gleichungen mit n Unbekannten) gelöst. Abgesehen davon, dass die Eigenschaften der Matrizen A und B den Lösungsalgorithmus bestimmen, darf man in diesem Fall davon ausgehen, dass sich der Backslash-Operator wie ein übliches Programm zur Lösung eines linearen Gleichungssystems verhält. Hierfür wird auf die Seite "Matlab: Zauberstab Backslash-Operator" verwiesen.
- Bei einer "breiten" Matrix A (mehr Unbekannte als Gleichungen) wird ein mögliches (zufälliges) Ergebnis abgeliefert, von dem das Gleichungssystem erfüllt wird. Bei dieser (praktisch kaum bedeutsamen) Variante muss man sich nur bewusst sein, dass es ein Ergebnis von unendlichen vielen Ergebnissen ist, die dieses Gleichungssystem hat.
- Bei einer "hohen" Matrix A wird in der Regel ein Ergebnis abgeliefert, von dem das Gleichungssystem nicht erfüllt wird. Allerdings wird damit das wichtige Spezialgebiet "Ausgleichsrechnung" bedient.
Vorsicht! Die Mächtigkeit des Backslash-Operators hat ihre Tücken.
Das Ergebnis kann die Lösung eines Gleichungssystems sein, kann eine beliebige Lösung (von unendlichen vielen Lösungen) sein, kann aber auch keine Lösung des Gleichungssystem sein, weil es im Sinne der Ausgleichsrechnung eine bestmögliche Annäherung ist.
Ob es eine gute Idee ist, diese unterschiedlichen Varianten in einen einzigen Operator zu packen, soll hier nicht diskutiert werden, aber: Der Alleskönner Backslash erspart dem Anwender nicht, ganz genau zu wissen, was er tut und was für ihn getan wird.

