Rundungsfehler, Nachiteration
 Die Darstellung der Zahlen und die Ausführung der Rechenoperationen im Computer mit einer endlichen Stellenanzahl führen unausweichlich zu numerischen Fehlern. Es wird also im Allgemeinen für das lineare Gleichungssystem
Die Darstellung der Zahlen und die Ausführung der Rechenoperationen im Computer mit einer endlichen Stellenanzahl führen unausweichlich zu numerischen Fehlern. Es wird also im Allgemeinen für das lineare Gleichungssystem
![]()
nur eine Näherung
![]()
ermittelt. Wenn diese in das Gleichungssystem wieder eingesetzt wird, so ergibt sich entsprechend
![]()
ein Restvektor, der wegen
![]()
mit
![]()
aus dem neuen Gleichungssystem
![]()
berechnet werden kann. Da sich die Koeffizientenmatrix gegenüber dem Ausgangssystem nicht geändert hat, kann dies bei Verwendung eines Eliminationsverfahrens (Gauß, Cholesky, ...) mit geringem Zusatzaufwand (nur Vorwärts- und Rückwärteinsetzen) erledigt werden. Diese Korrektur (Nachiteration) kann gegebenenfalls mehrmals ausgeführt werden, aber:
Die Nachiteration führt im Allgemeinen nur dann zu einer spürbaren Verbesserung des Ergebnisses, wenn der Prozess mit einer höheren Genauigkeit als die Erstrechnung ausgeführt wird.
Die Qualität der Lösung eines linearen Gleichungssystems mit Hilfe eines direkten Verfahrens und die Konvergenzgeschwindigkeit iterativer Verfahren hängen wesentlich von der so genannten "Kondition" der Koeffizientenmatrix A ab. Diese kann mit einer "Konditionszahl" quantitativ gemessen werden. Sie wird definiert als Produkt aus einer Norm der Matrix A und der Norm ihrer Inversen:
![]()
Für singuläre Matrix A gilt: cond(A) = ∞. Matrixnormen werden analog zu Vektornormen definiert, wobei die Forderung
![]()
hinzukommt. Ein Beispiel für eine Matrixnorm ist das "Maximum der mit den Absolutwerten gebildeten Zeilensummen":
![]()
Es lässt sich zeigen, dass die Konditionszahl folgendermaßen gedeutet werden kann:
Bei Rechnung mit einer festen Anzahl wesentlicher Dezimalstellen ist im Ergebnis eine Abweichung von cond(A) Einheiten der letzten Dezimalstelle möglich.
Eine zusätzliche Fehlerquelle ergibt sich dadurch, dass schon das Ausgangssystem wegen der begrenzten Stellenanzahl der Darstellung im Computer mit einem Fehler behaftet ist (Anfangsabbrechfehler). Die dadurch hervorgerufenen Fehler im Ergebnis sind von gleicher Größenordnung wie die Fehler, die durch den Lösungsprozess erzeugt werden.
Man beachte das Beispiel, das die Auswirkungen einer schlecht konditionierten Matrix demonstriert und die Möglichkeit, die Kondition einer Koeffizientenmatrix eines Gleichungssystems durch Skalierung zu verbessern.
Kondition einer symmetrischen, positiv definiten Matrix
Für den Sonderfall der symmetrischen, positiv definiten Matrix kann die Konditionszahl nach
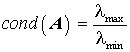
(Verhältnis des größten zum kleinsten Eigenwert der Matrix A) berechnet werden. Nach der oben für den allgemeinen Fall getroffenen Aussage (über die unsicheren Einheiten der letzten Dezimalstelle) sollte man mit der Konditionszahl etwas allgemeiner die Anzahl der "unsicheren Dezimalstellen u" entsprechend
![]()
(lg ist der dekadische Logarithmus) ermitteln.
Für die Berechnung der Eigenwerte bieten sich die Iterationsverfahren auf der Basis der von-Misesschen Vektoriteration an. Weil es ohnehin nur um Abschätzungen geht, genügen wenige Iterationen.

