Unvollständige Cholesky-Zerlegung ("Incomplete Cholesky")
Für das Verfahren der konjugierten Gradienten, das Symmetrie und positive Definitheit der Koeffizientenmatrix voraussetzt, kann eine Präkonditionierung auf der Basis der unvollständigen Cholesky-Zerlegung der dünn besetzten Matrix vorgenommen werden. In der "klassischen Variante" werden dabei nur genau die Elemente in der Dreiecksmatrix erzeugt, auf deren Positionen auch in der Ausgangsmatrix von Null verschiedene Elemente stehen.
Matlab offeriert mit der Function cholinc sowohl diese Variante als auch (eigentlich alle möglichen) Varianten, bei denen die entstehende Dreiecksmatrix sowohl weniger als auch mehr Elemente enthält. Nachfolgend wird die Matlab-Function pcg ("Preconditiones conjugate gradients") mit Präkonditionierern aufgerufen, die mit cholinc erzeugt werden. Als Gleichungssysteme werden die FEM-Systeme verwendet, die sich bei den Testrechnungen ohne Präkonditionierung durch schlechte Konvergenz auszeichneten.
Zweidimensionales Rahmentragwerk
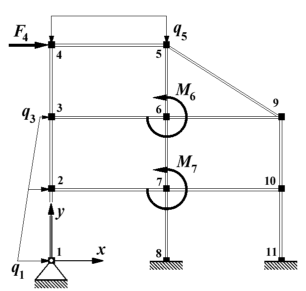
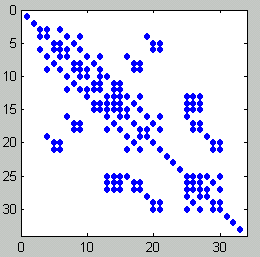Nebenstehend links ist der ebene biege- und dehnsteife Rahmen dargestellt (Beispiel aus dem Kapitel "Verifizieren von Computerrechnungen"), dessen FEM-Modell in der Datei Rahm17.dat gespeichert ist. Es ist ein sehr kleines Problem, das auf ein Gleichungssystem mit nur 33 Gleichungen führt (rechts das Belegungsmuster der Koeffizientenmatrix mit den von Null verschiedenen Elementen), das allerdings einigen Iterationsverfahren (siehe "Testrechnungen für iterative Verfahren (1)") erhebliche Probleme bereitete.
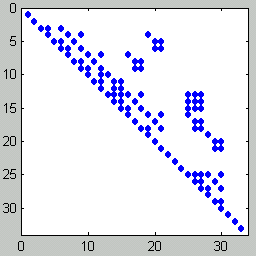
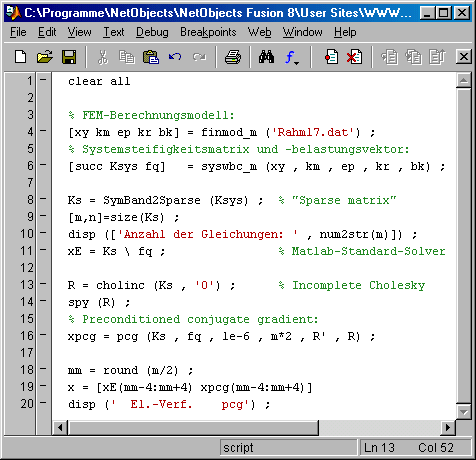
Mit der einfachsten Präkonditionierung (Skalierung) konvergierte das Verfahren wesentlich besser. Hier soll nun die Präkonditionierung mit "Incomplete Cholesky" in der "klassischen Variante" realisiert werden (Belegungsmuster mit von Null verschiedenen Elementen der Dreiecksmatrix der Cholesky-Zerlegung ist identisch mit dem entsprechenden Dreieck der Ausgangsmatrix). Matlab bietet dafür die Aufrufvariante, die im nachstehend zu sehenden Matlab-Script PraeCondCholInc1.m in Zeile 13 zu sehen ist. Die Ausgabe des Belegungsmusters in Zeile 14 (rechtes Bild) bestätigt dies:
 |
|
Im Aufruf von pcg in Zeile 16 werden die Ergebnismatrix der unvollständigen Cholesky-Zerlegung und deren Transponierte als Präkonditionierer an das Iterationsverfahren übergeben. Das Ergebnis bestätigt die Erwartungen: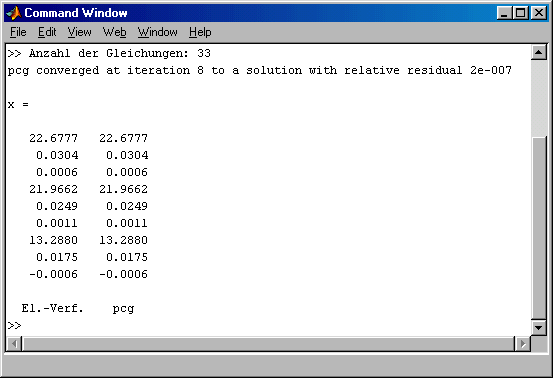
Das Verfahren, das bei diesem kleinen Beispiel ohne Präkonditionierung erst nach 62 Iterationsschritten konvergierte und bei Präkonditionierung durch Skalierung nach 24 Iterationsschritten konvergierte, beendet die Arbeit nach Präkonditionierung mit "Incomplete Cholesky" bereits nach 8 Iterationsschritten erfolgreich.
Andererseits verlagert man dabei doch einen erheblichen Teil der Arbeit vom Iterationsprozess zur Präkonditionierung, denn zumindest bei diesem kleinen Beispiel ist der Aufwand für "Incomplete Cholesky" nicht wesentlich geringer als für die komplette Cholesky-Zerlegung, mit der man dann ja den wesentlichen Aufwand dieses direkten Lösungsverfahrens bereits erledigt hätte. Deshalb soll noch ein größeres Gleichungssystem untersucht werden.
Dreidimensionales Tragwerk mit biege-, dehn- und torsionssteifen Elementen
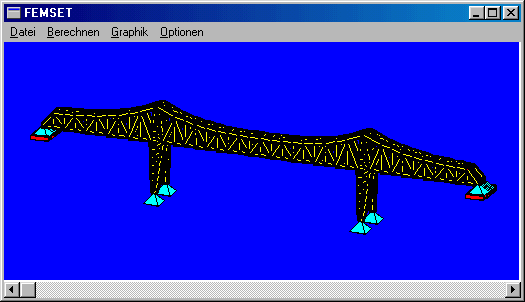Das nebenstehend zu sehende Finite-Elemente-Modell der Brücke über den Nord-Ostsee-Kanal bei Rendsburg besteht aus 1947 Elementen (biege-, dehn- und torsionssteife Träger mit je zwei Knoten), die an 747 Knoten untereinander verbunden sind. Dieses Modell führt auf ein (im Vergleich mit typischen FEM-Modellen eher kleines) Gleichungssystem mit 4482 Unbekannten.
Das FEM-Berechnungsmodell ist in der Datei Rendbrem.dat gespeichert. Bei Verwendung des oben für das 2D-Problem benutzte Matlab-Scripts PraeCondCholInc1.m, wobei nur in Zeile 4 der Name der Datei Rahm17.dat durch Rendbrem.dat zu ersetzen ist, wird man durch die folgende Fehlermeldung darauf aufmerksam gemacht, dass "Incomplete Cholesky" in der klassischen Variante auch für symmetrische und positiv definite Matrizen nicht immer realisierbar ist:
Matlab bietet aber noch andere Aufrufvarianten für die Function cholinc an, speziell kann als zweiter Parameter eine "Drop tolerance" angegeben werden, mit der der Füllungsgrad der Dreiecksmatrix innerhalb der sinnvollen Grenzen beinahe beliebig gesteuert werden kann (es können also auch deutlich weniger Elemente entstehen als bei der klassischen Variante, andererseits auch wesentlich mehr). In den beiden Extremfällen erhält man eine reine Digonalmatrix bzw. das Ergebnis der kompletten Cholesky-Zerlegung.
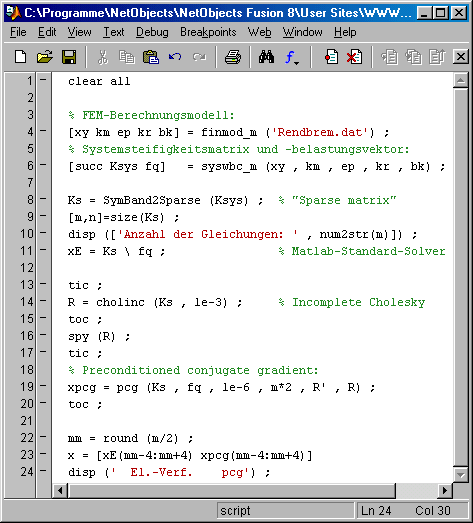Das nebenstehend zu sehende Matlab-Script PraeCondCholInc2.m realisiert diese Variante mit einer "Drop tolerance" von 10-3 (Zeile 14). Das Belegungsmuster (von Null verschiedene Elemente) des Ergebnisses der unvollständigen Cholesky-Zerlegung wird in Zeile 16 ausgegeben:
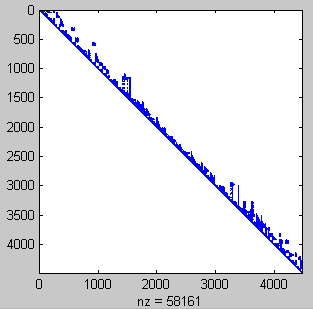
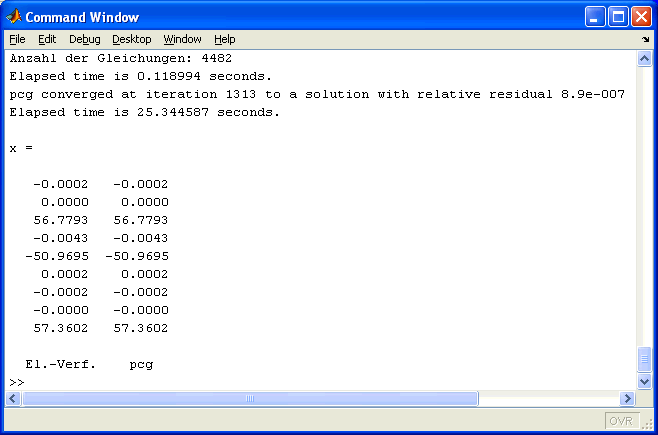
Mit 58161 von Null verschiedenen Elementen ist diese Rechtsdreiecksmatrix etwas stärker besetzt als das obere Dreieck der symmetrischen Koeffizientenmatrix, das 43580 Elemente enthält (also etwas stärker gefüllt als bei "Incomplete Cholesky" in der klassischen Variante). Das Ergebnis im Command Window entsteht nach 1313 Iterationsschritten. Dies ist mehr als bei der entsprechenden Rechnung mit reiner Skalierung:
Das Matlab-Script wurde zusätzlich mit einigen tic- und toc-Aufrufen ausgestattet, um den relativen Anteil des Aufwandes für cholinc und pcg zu ermitteln. Mit verschiedenen Werten für die "Drop tolerance" zwischen 0 und 1 ergaben sich unterschiedlich stark besetzte Rechtsdreiecksmatrizen als Ergebnis der unvollständigen Cholesky-Zerlegung von der reinen Diagonalmatrix ("Drop tolerance" gleich 1) bis zum Ergebnis der kompletten Cholesky-Zerlegung ("Drop tolerance" 0). Die folgende Tabelle zeigt die Ergebnisse einiger Testrechnungen:
|
Dass mit zunehmender Qualität der unvollständigen Cholesky-Zerlegung (hier zu messen an der Anzahl der von Null verschiedenen Elemente nz in der Rechtsdreiecksmatrix) die Präkonditionierung zu schnellerer Konvergenz führt, war zu erwarten. Die beiden Extremwerte sind bemerkenswert:
- Mit der "Drop tolerance" 1 entsteht eine reine Diagonalmatrix als Präkonditionierer, der den Iterationsprozess auf genau die 915 Schritte beschleunigt, die bei den Testrechnungen mit Skalierung benötigt wurden. Kleinere Werte für die "Drop tolerance" liefern mit aufwendiger zu erzeugenden Präkonditionierern zunächst deutlich mehr Iterationsschritte.
- Mit der "Drop tolerance" 0 entsteht die komplette Rechtsdreiecksmatrix der vollständigen Cholesky-Zerlegung, die natürlich dazu führt, dass Konvergenz im ersten Schritt erreicht wird (dieser Fall ist eigentlich die Lösung des Gleichungssystems mit dem Cholesky-Verfahren). Die benötigten Rechenzeiten für die iterative Lösung werden mit aufwendiger werdender Präkonditionierung erwartungsgemäß immer kleiner, aber bei diesem Beispiel ist der Aufwand der vollständigen Cholesky-Zerlegung (und damit die Lösung des Gleichungssystems mit diesem direkten Verfahren) nicht zu unterbieten.
Download
Die Matlab-Scripts auf dieser Seite und die von ihnen aufgerufenen Functions, DLLs und Dateien sind zum Download verfügbar:
- Die gezeigten Matlab-Scripts sind als PraeCondCholInc1.m und PraeCondCholInc2.m verfügbar.
- Zusätzlich werden die DLLs finmod_m.dll und syswbc_m.dll und die Matlab-Function SymBand2Sparse.m benötigt. Die FEM-Modelle befinden sich in den Dateien Rahm17.dat (2D-Rahmen) und Rendbrem.dat (3D-Tragwerk).
