Aufgabe: Eigenschwingungen eines kontinuierlich mit Masse belegten Biegeträgers
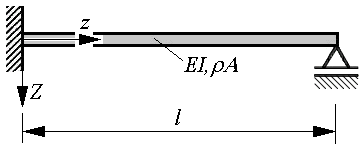 Das Entstehen und der Umgang mit homogenen Gleichungssystemen wird hier am besonders einfachen Beispiel der Berechnung der Eigenschwingungen eines kontinuierlich mit Masse belegten Biegeträgers demonstriert (zu komplizierteren Beispielen kommt man über den Link "Biegeschwingungen gerader Träger").
Das Entstehen und der Umgang mit homogenen Gleichungssystemen wird hier am besonders einfachen Beispiel der Berechnung der Eigenschwingungen eines kontinuierlich mit Masse belegten Biegeträgers demonstriert (zu komplizierteren Beispielen kommt man über den Link "Biegeschwingungen gerader Träger").
Für den nebenstehend skizzierten Träger sollen bei der numerischen Auswertung folgende Zahlenwerte angenommen werden:
l = 1 m ; EI = 3000 Nm2 ; ρA = 3 kg/m .
Analytische Lösung ⇒ Homogenes Gleichungssystem
Im Skript "Biegeschwingungen gerader Träger" (PDF) wird die Theorie ausführlich dargestellt und gezeigt, dass sich die Eigenschwingungsformen in dem oben dargestellten Koordinatensystem in der Form
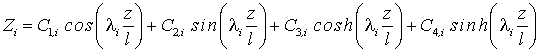
aufschreiben lassen (es gibt bei diesem System mit "unendlich vielen Freiheitsgraden" unendlich viele Eigenfrequenzen mit jeweils einer zugehörigen Schwingungsform, der Index i bezieht sich auf die i-te Schwingungsform). Die darin enthaltenen Parameter λi sind mit den Eigenkreisfrequenzen der Schwingungen über die Beziehung
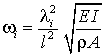
verknüpft, und die Konstanten C1,i bis C4,i sind die Lösungen des homogenen Gleichungssystems
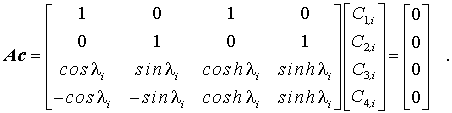
Natürlich interessieren nur die nichttrivialen Lösungen, denn die triviale Lösung beschreibt nur die Ruhelage des Systems. Schwingungen sind also nur möglich, wenn die Koeffizientenmatrix A singulär ist, ihre Determinante den Wert Null hat. Die Bedingung
![]()
führt auf die Bestimmungsgleichung für die λi-Werte, die für diesen einfachen Fall durch Entwicklung der Determinante erzeugt werden kann:
![]()
liefert die λi-Werte, für die das homogene Gleichungssystem nichttriviale Lösungen hat. Die numerische Lösung dieser Gleichung mit Matlab wird bei der exakten Lösung der Aufgabe 32-6 auf verschiedene Weise realisiert (siehe auch: "Matlab: Beispiel einer Nullstellenberechnung"). Die Gleichung hat unendlich viele Lösungen, die drei kleinsten sind:
λ1 = 3,9266 ; λ2 = 7,0686 ; λ3 = 10,2102 ; ...
Für jedes λi ist die Koeffizientenmatrix A des homogenen Gleichungssystems singulär. Damit kann für jedes λi ein Satz nichttrivialer Konstanten C1,i bis C4,i (bis auf einen beliebigen Faktor) berechnet werden, so dass die zugehörige Eigenschwingungsform Zi nach der oben angegebenen Formel aufgeschrieben werden kann. In Matlab ist das z. B. zu realisieren durch den Aufruf der null-Function, der entsprechend
ci = null (Ai)
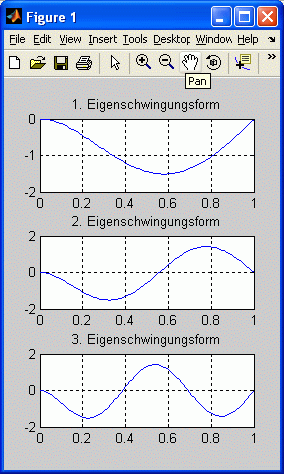
die Matrix Ai (berechnet mit dem Wert für λi) übergeben wird. Abgeliefert wird der Vektor der 4 Konstanten C1,i bis C4,i. Nebenstehend sind die graphischen Darstellungen der Schwingungsformen für die ersten drei Eigenfrequenzen zu sehen.
Differenzenverfahren ⇒ Spezielles Matrizeneigenwertproblem
Im Skript "Biegeschwingungen gerader Träger" (PDF) wird die hier betrachtete Aufgabe auch mit verschiedenen numerischen Verfahren gelöst (Differenzenverfahren, Verfahren von Ritz und Finite-Elemente-Methode). Diese Verfahren führen auf spezielle Varianten des homogenen Gleichungssystems.

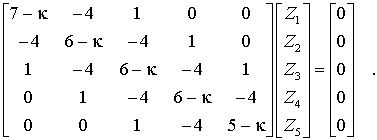
In
![]()
steckt (neben den gegebenen Größen und der Schrittweite h) wieder die Eigenkreisfrequenz. Natürlich interessieren auch hier nur die nichtttrivialen Lösungen des homogenen Gleichungssystems. Gesucht sind also die κ-Werte, die die Koeffizientenmatrix singulär machen. Man könnte also die Determinante dieser Matrix nach dem Laplaceschen Entwicklungssatz berechnen, was auf eine algebraische Gleichung 5. Grades führen würde, die man dann numerisch lösen müsste. Dies ist nicht empfehlenswert (und für feinere Diskretisierungen, die auf wesentlich größere Gleichungssysteme führen, ohnehin nicht praktikabel), denn mit dieser Form eines homogenen Gleichungssystems beschäftigt sich ausführlich ein Spezialgebiet der numerischen Mathematik und stellt leistungsfähige Algorithmen zur Verfügung. Dafür wird es in der Form
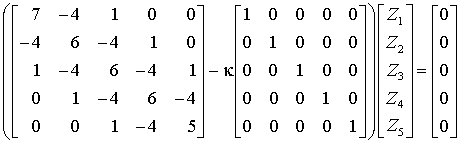
geschrieben. Es ist ein so genanntes "Spezielles Matrizeneigenwertproblem"
![]()
(E ist die Einheitsmatrix). Für die Lösung solcher Aufgabenstellungen wird auf die Seite "Matrizeneigenwertprobleme" verwiesen. Die Ergebnisse findet man hier unter dem Link "Lösung mit dem Differenzenverfahren mit Matlab".
Finite-Elemente-Methode ⇒ Allgemeines Matrizeneigenwertproblem
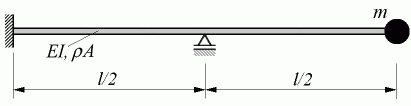 Im Skript "Biegeschwingungen gerader Träger" (PDF) wird die nebenstehend skizzierte Aufgabe als Beispiel für die Lösung mit der Finite-Elemente-Methode ausführlich behandelt. Als Zahlenwerte werden verwendet:
Im Skript "Biegeschwingungen gerader Träger" (PDF) wird die nebenstehend skizzierte Aufgabe als Beispiel für die Lösung mit der Finite-Elemente-Methode ausführlich behandelt. Als Zahlenwerte werden verwendet:
l = 1 m ; EI = 3000 Nm2 ; ρA = 3 kg/m ; m = 2 kg .
Wie beim Differenzenverfahren wird die Schwingungsform durch Variablen an diskreten Punkten beschrieben (hier: Verschiebungen und Tangentenneigungen).
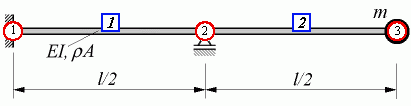 In dem genannten Skript wird gezeigt, dass bei einer (sehr groben) Einteilung des Träger in nur 2 Elemente (nebenstehende Skizze) ein homogenes Gleichungssystem mit nur 3 Gleichungen entsteht, weil 2 Verschiebungen (an der Einspannung links und an der Zwischenstütze) und die Tangentenneigung an der Einspannung links gleich Null sind, so dass die 3 verbleibenden unbekannten Verformungen die Tangentenneigungen an der Zwischenstütze (Punkt 2) und am rechten Rand (Punkt 3) und die Vertikalverschiebung des Punktes 3 sind. Das verbleibende homogene Gleichungssystem wird hier gleich in der Form des Matrizeneigenwertproblems aufgeschrieben:
In dem genannten Skript wird gezeigt, dass bei einer (sehr groben) Einteilung des Träger in nur 2 Elemente (nebenstehende Skizze) ein homogenes Gleichungssystem mit nur 3 Gleichungen entsteht, weil 2 Verschiebungen (an der Einspannung links und an der Zwischenstütze) und die Tangentenneigung an der Einspannung links gleich Null sind, so dass die 3 verbleibenden unbekannten Verformungen die Tangentenneigungen an der Zwischenstütze (Punkt 2) und am rechten Rand (Punkt 3) und die Vertikalverschiebung des Punktes 3 sind. Das verbleibende homogene Gleichungssystem wird hier gleich in der Form des Matrizeneigenwertproblems aufgeschrieben:
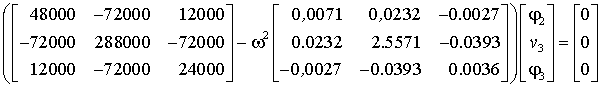
(ω ist die Eigenkreisfrequenz des Schwingungssystems). Dies ist ein so genanntes "Allgemeines Matrizeneigenwertproblem"
![]()
(im Gegensatz zum speziellen Matrizeneigenwertprolem, wie es oben beim Differenzenverfahren entstand, ist beim allgemeinen Eigenwertproblem keine der beiden Matrizen eine Einheitsmatrix).
Für die Lösung solcher Aufgabenstellungen wird auch hier auf die Seite "Matrizeneigenwertprobleme" verwiesen. Die Ergebnisse findet man u. a. auf der Seite "Beispiel: Eigenschwingungen eines geraden Biegeträgers".

