Bandmatrizen: LR-Zerlegung und Cholesky-Zerlegung
Bandmatrizen
Unsymmetrische Bandmatrix
 enthalten nur in einem relativ schmalen Band in der Umgebung der Hauptdiagonalen von Null verschiedene Elemente. Finite-Elemente-Berechnungen und Rechnungen mit dem Differenzenverfahren führen in der Regel auf (sehr große) lineare Gleichungssysteme, deren Koeffizientenmatrizen Bandmatrizen sind.
enthalten nur in einem relativ schmalen Band in der Umgebung der Hauptdiagonalen von Null verschiedene Elemente. Finite-Elemente-Berechnungen und Rechnungen mit dem Differenzenverfahren führen in der Regel auf (sehr große) lineare Gleichungssysteme, deren Koeffizientenmatrizen Bandmatrizen sind.
 Sowohl bei der
LR-Zerlegung des verketteten Algorithmus
bei beliebiger (regulärer) quadratischer Matrix als auch beim
Cholesky-Verfahren
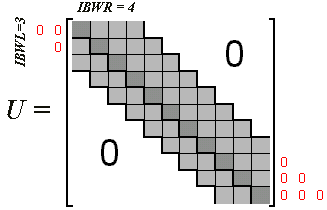
für symmetrische (positiv definite) Matrix überträgt sich die Bandeigenschaft der Koeffizientenmatrix A auf die Dreiecksmatrizen L bzw. R. Das nebenstehend zu sehende Beispiel demonstriert dies für die Cholesky-Zerlegung einer 6*6-Matrix mit der (halben) Bandweite ib = 3.
Sowohl bei der
LR-Zerlegung des verketteten Algorithmus
bei beliebiger (regulärer) quadratischer Matrix als auch beim
Cholesky-Verfahren
für symmetrische (positiv definite) Matrix überträgt sich die Bandeigenschaft der Koeffizientenmatrix A auf die Dreiecksmatrizen L bzw. R. Das nebenstehend zu sehende Beispiel demonstriert dies für die Cholesky-Zerlegung einer 6*6-Matrix mit der (halben) Bandweite ib = 3.
Die Programmierung der Algorithmen für Gleichungssysteme mit Bandmatrizen muss die spezielle kompakte Speicherungsform berücksichtigen und überflüssige Operationen vermeiden (dies sind im Wesentlichen die Additionen von Nullelementen und die Multiplikationen, bei denen ein Faktor Null ist (es wird also nur innerhalb des Bandes gerechnet). Folgende Algorithmen sind verfügbar:
- Gauß-Algorithmus (mit Pivotisierung) zur Lösung eines linearen Gleichungssystems mit beliebiger (nicht symmetrischer) quadratischer Bandmatrix (Matlab function).
- Cholesky-Zerlegung einer symmetrischen positiv defniten Bandmatrix (aus Matlab aufrufbare DLL, zwei Beispiele).
- Cholesky-Verfahren zur Lösung eines linearen Gleichungssystems mit symmetrischer positiv defniter Bandmatrix (aus Matlab aufrufbare DLL, zwei Beispiele).
Der Aufwand reduziert sich durch die Ausnutzung der Bandstruktur erheblich. Während für die Cholesky-Zerlegung mit voll besetzter Matrix n*n-Matrix etwa n3/6 Multiplikationen und Additionen erforderlich sind, fallen bei einer Bandmatrix nur etwa n*(ib)2/6 Multiplikationen und Additionen an. Es lohnt sich also, speziell die quadratisch den Aufwand beeinflussende Bandweite möglichst klein zu halten. Weil allerdings das am weitesten von der Hauprtdiagonalen entfernte Element die Bandweite bestimmt, kann schon ein einziges Element die Bandweite wesentlich vergrößern, was unbedingt vermieden werden sollte.
Verfahren zur Reduzierung der Bandweite können den Aufwand drastisch verringern,
siehe hierzu "Reduzierung von Bandweite und Fill-in".
Weitere deutliche Reduzierung des Aufwands: Skyline-Verfahren, "Fill-in-Problem"
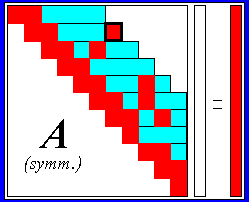
 Das nebenstehende Schema links zeigt die typische Struktur eines FEM-Gleichungssystems. Rot eingezeichnet sind (nur für das rechte obere Dreieck der symmetrischen Koeffizientenmatrix A) die Nicht-Null-Elemente. Das fett schwarz umrandete Element bestimmt die Bandweite, so dass auch innerhalb des Bandes zahlreiche (hellblau gezeichnete) Elemente existieren.
Das nebenstehende Schema links zeigt die typische Struktur eines FEM-Gleichungssystems. Rot eingezeichnet sind (nur für das rechte obere Dreieck der symmetrischen Koeffizientenmatrix A) die Nicht-Null-Elemente. Das fett schwarz umrandete Element bestimmt die Bandweite, so dass auch innerhalb des Bandes zahlreiche (hellblau gezeichnete) Elemente existieren.
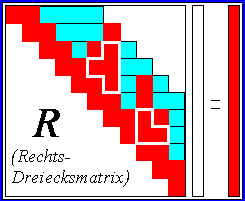
Das Schema rechts zeigt die Situation nach der Cholesky-Zerlegung der Matrix A. Die Rechts-Dreiecksmatrix R enthält nur wenige (die weiß umrandeten) zusätzliche Nicht-Null-Elemente: Nur die Null-Elemente innerhalb des Bandes, die ein Nicht-Null-Element über sich haben, werden selbst zu Nicht-Null-Elementen ("Fill-in"-Problem), alle anderen Null-Elemente bleiben bei der Cholesky-Zerlegung erhalten.
Diese Tatsache kann genutzt werden, um eine weitere deutliche Verringerung des Aufwandes zu erzielen.
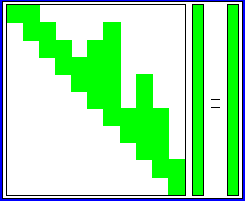 Skyline-Methode
Skyline-Methode
Es werden nur die Elemente innerhalb der "Skyline" der Koeffizientenmatrix gespeichert (nebenstehendes Schema), und die Operationen bei der Cholesky-Zerlegung brauchen sich auch nur auf diese Elemente zu beziehen. Während bei der Bandspeicherung die Gleichungen so angeordnet sein sollten, dass eine möglichst kleine Bandweite entsteht, sollte beim "Skyline-Verfahren" ein möglichst geringes "Fill-in" entstehen. Es gibt eine Reihe von "Umordnungs-Strategien" für lineare Gleichungssysteme, die entweder die Bandweite oder aber das "Fill-in" verringern. Die theoretisch durchaus gegebene Möglichkeit, das jeweilige Minimum zu erreichen, ist für große Systeme nicht praktikabel, für kleinere Systeme lohnt es sich nicht. Bei Verzicht darauf, die bestmögliche Anordnung der Gleichungen zu finden, kann oft mit geringem Aufwand ein großer Effekt erzielt werden. siehe hierzu: "Reduzierung von Bandweite und Fill-in".
Geringster Speicherbedarf: "Sparse-Matrix-Speicherung" und "Fill-in-Problem"
Die allgemeine "Sparse Matrix"-Speicherung, wie sie z. B. in Matlab realisiert ist, geht noch einen Schritt weiter: Es werden nur die Nicht-Null-Elemente und zu jedem Element das zugehörige Indexpaar (Position des Elementes in der Matrix) gespeichert (die Menge aller Indexpaare der Nicht-Null-Elemente wird "Besetzungsstruktur" der Matrix genannt). Diese Variante ist natürlich ideal, wenn sich die "Besetzungsstruktur" der Matrix während des Berechnungsprozesses nicht ändert (wie z. B. bei den Iterationsverfahren zur Lösung von Gleichungssystemen oder beim "Incomplete Cholesky"-Verfahren).
 Beim Cholesky-Verfahren ist diese Speichervariante weitgehend gleichwertig mit der oben beschriebenen "Skyline"-Methode: Das "Fill-in" sorgt für zusätzlich erforderliche Speicherplätze während des Algorithmus und der erforderliche Aufwand ist vergleichbar. Bei der "Skyline"-Variante wird das "Fill-in" gewissermaßen vorausgedacht, und es sind von vornherein zusammenhängende Bereiche vorhanden (die vertikalen "Schornsteine", die als Vektoren gespeichert werden), was einer effektiven Programmierung entgegenkommt. Andererseits sollte natürlich am Start des Cholesky-Verfahrens für eine "Sparse matrix" die Prognose für die erforderlichen Speicherbereiche stehen, die dann in einem Schritt auch organisiert werden (auf keinen Fall sollte jedes beim "Fill-in" entstehende Element eine Speicherplatzanforderung auslösen), und damit sind diese beiden Speichervarianten weitgehend gleichwertig.
Beim Cholesky-Verfahren ist diese Speichervariante weitgehend gleichwertig mit der oben beschriebenen "Skyline"-Methode: Das "Fill-in" sorgt für zusätzlich erforderliche Speicherplätze während des Algorithmus und der erforderliche Aufwand ist vergleichbar. Bei der "Skyline"-Variante wird das "Fill-in" gewissermaßen vorausgedacht, und es sind von vornherein zusammenhängende Bereiche vorhanden (die vertikalen "Schornsteine", die als Vektoren gespeichert werden), was einer effektiven Programmierung entgegenkommt. Andererseits sollte natürlich am Start des Cholesky-Verfahrens für eine "Sparse matrix" die Prognose für die erforderlichen Speicherbereiche stehen, die dann in einem Schritt auch organisiert werden (auf keinen Fall sollte jedes beim "Fill-in" entstehende Element eine Speicherplatzanforderung auslösen), und damit sind diese beiden Speichervarianten weitgehend gleichwertig.
In Matlab ist diese Speichervariante für zahlreiche Operationen verfügbar und außerordentlich effektiv realisiert.
 Das folgende kleine Matlab-Script demonstriert die "Sparse Matrix"-Speicherung und das "Fill-in" an einem kleinen Beispiel:
Das folgende kleine Matlab-Script demonstriert die "Sparse Matrix"-Speicherung und das "Fill-in" an einem kleinen Beispiel:
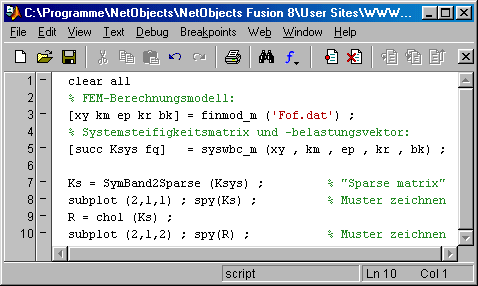
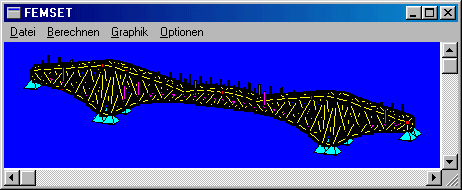
In der Zeile 3 wird das FEM-Berechnungsmodell der oben dargestellten Brückenkonstruktion von der Datei Fof.dat eingelesen, in Zeile 5 wird daraus das lineare Gleichungssystem mit Matlab-Femset erzeugt.
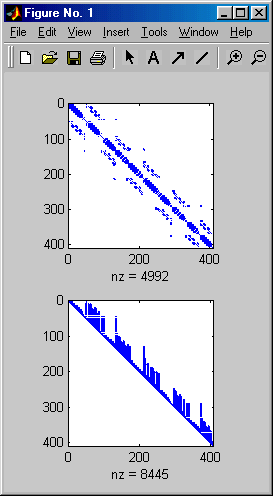
In Zeile 7 wird die (symmetrische und postiv definite) Koeffizientenmatrix in das Matlab-"Sparse Matrix"-Format umgewandelt, in Zeile 9 wird die Cholesky-Zerlegung ausgeführt. Rechts sieht man die beiden Belegungsmuster der (symmetrischen) Ausgangsmatrix und der nach Cholesky erzeugten Rechtsdreiecksmatrix. Deutlich sieht man, dass sich die "Schornsteine" (wie oben beim Skyline-Verfahren beschrieben) weitgehend gefüllt haben.
Die Vorteile der beschriebenen Speichervarianten zeigen sich natürlich erst bei großen Gleichungssystemen. Dies wird auf der Seite "Band", "Skyline", "Sparse" und "Voll" demonstriert.
Verfahren zur Reduzierung des Fill-in können den Aufwand drastisch verringern,
siehe hierzu "Reduzierung von Bandweite und Fill-in".
Download
Das Matlab-Script für die Demonstration der "Sparse Matrix"-Speicherung und die darin aufgerufenen DLLs, Function und Datei sind zum Download verfügbar:
- Das gezeigte Matlab-Script ist als SparsTestFof.m verfügbar.
- Zusätzlich werden die DLLs finmod_m.dll und syswbc_m.dll und die Matlab-Function SymBand2Sparse.m benötigt. Das FEM-Modell befindet sich in der Datei Fof.dat.

