Für das Verständnis der nachfolgend gegebenen Definitionen ist es sicher hilfreich, wenn man sich den zweidimensionalen bzw. dreidimensionalen Vektorraum vorstellt, weil sich darin alle Aussagen, die formal für den n-dimensionalen Raum gemacht werden, geometrisch deuten lassen.
Der n-dimensionale Vektorraum
Die Gesamtheit aller n-dimensionalen Vektoren (Vektoren mit n Komponenten) wird n-dimensionaler Vektorraum genannt. Die Komponenten der Vektoren rekrutieren sich aus einem Zahlenkörper (z. B. dem Zahlenkörper der reellen Zahlen). Vektoren sind im Regelfall Spaltenvektoren
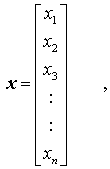
können jedoch auch als Zeilenvektoren in der Form
![]()
(sprich: "x-transponiert") geschrieben werden.
Lineare Unabhängigkeit, Linearkombination
Die Vektoren x1, x2, x3, ... , xm werden linear unabhängig genannt, wenn ihre so genannte Linearkombination
![]()
nur für c1 = c2 = c3 = ... = cm = 0 den Nullvektor y = o ergibt (alle Komponenten eines Nullvektors sind gleich Null), sonst linear abhängig.
Basis, Einheitsvektoren, Koordinaten
Mehr als n Vektoren des n-dimensionalen Vektorraums sind immer linear abhängig. Ein System von genau n linear unabhängigen Vektoren wird Basis genannt. Jeder beliebige Vektor kann als Linearkombination einer Basis dargestellt werden. Die Koeffizienten ci dieser Linearkombination heißen Koordinaten des Vektors bezüglich der Basis. Speziell bildet das System der n Einheitsvektoren
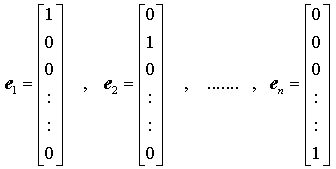
eine Basis, für die die Komponenten eines Vektors zugleich seine Koordinaten sind.
Euklidischer Vektorraum, Metrik (Betrag, Winkel, Orthogonalität)
Ein Vektorraum, für den ein inneres Produkt (Skalarprodukt) zweier Vektoren in der Form
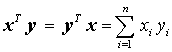
definiert ist, heißt Euklidischer Vektorraum. Mit Hilfe dieser Beziehung wird in Anlehnung an die Begriffe des dreidimensionalen Raums eine Metrik eingeführt. Man definiert
![]()
als Betrag (auch: Länge) des Vektors x und
![]()
als Abstand der Vektoren x und y. Der Begriff des Winkels φ zwischen zwei Vektoren ist durch die Gleichung
![]()
gegeben. Zwei Vektoren x und y sind also zueinander orthogonal (stehen rechtwinklig aufeinander, kein Vektor besitzt eine Komponente in Richtung des anderen Vektors), wenn
![]()
gilt.
Orthogonalsystem, Orthonormalsystem, Orthonormalmatrix, Vektornormen
- Ein Satz Vektoren, die sämtlich zueinander orthogonal sind, heißt orthogonales System. Vektoren eines orthogonalen Systems sind stets linear unabhängig. Im n-dimensionalen Vektorraum existiert immer ein System von n orthogonalen Vektoren (vollständiges Orthogonalsystem).
- Einen Vektor vom Betrage Eins nennt man normiert, ein Orthogonalsystem mit ausschließlich normierten Vektoren ist ein Orthonormalsystem. Die oben angegebenen besonders einfachen n Einheitsvektoren des n-dimensionalen euklidischen Vektorraums sind ein Beispiel für eine orthonormierte Basis.
- Eine Matrix, deren Spalten ausschließlich zueinander othonormierte Vektoren sind, heißt Orthonormalmatrix
- Eine so genannte Vektornorm ||x|| hat die Eigenschaften:
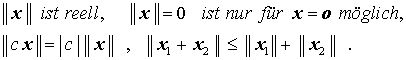
Der Betrag eines Vektors erfüllt z. B. augenscheinlich sämtliche Bedingungen für eine Vektornorm.

