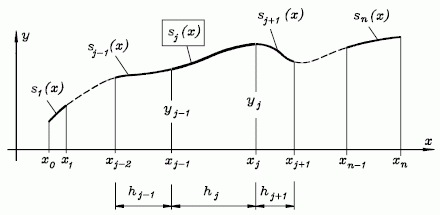
Ansatzfunktionen
Auf der Seite "Natürliche Splines" werden die Bedingungen formuliert, die für die Interpolation einer vorgegebenen Punktmenge ("Stützpunkte") mit "natürlichen Spline-Funktionen" (Polynome 3. Grades) erfüllt sein müssen. Der dort hergeleitete Algorithmus zur Berechnung der Koeffizienten der Polynome versagt, wenn der Abstand zwischen zwei aufeinanderfolgenden Stützstellen hj ≤ 0 ist. Damit sind zum Beispiel geschlossene Kurven nicht darstellbar.
Als Lösung dieses Problems bietet sich die Parameterdarstellung der Funktionen an. An die Stelle der Ansatzfunktion sj(x) = y(x) treten
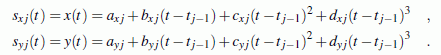
Für die Stützstellen gilt, dass alle Wertepaare (xj,yj) durch jeweils zwei Wertepaare (xj,tj) und (yj,tj) ersetzt werden, wobei man bei der Festlegung der tj-Werte ziemlich frei ist. Besonders einfach wird es, wenn man dem Parameter t eine konstante Schrittweite von Stützpunkt zu Stützpunkt zuweist:
![]()
was zweckmäßig zum Beispiel so realisiert wird, dass für alle tj−1 = j gesetzt wird, so dass die Klammern in den Ansatzfunktionen an den Rändern eines Spline-Abschnitts die Werte 0 bzw. 1 annehmen.
Berechnung der Spline-Funktionen für offene Splines
Bei Splineansätzen in Parameterdarstellung fällt die doppelte Anzahl zu bestimmender Parameter an. Weil für sxj(t) und syj(t) formal gleichartige Ansätze gewählt werden, muss der Algorithmus für die Berechnung der Koeffizienten zweimal abgespult werden. Es ist allerdings kaum ein Mehraufwand, weil der aufwendigste Teil, die Lösung des Gleichungssystems zur Bestimmung der cj mit der gleichen Koeffizientenmatrix für beide Rechnungen ausgeführt werden muss.
Der komplette Algorithmus wird unter Berücksichtigung der oben beschriebenen Vereinfachungen noch einmal zusammengestellt. Zunächst müssen die cxj und cyj aus folgendem Gleichungssystem berechnet werden:
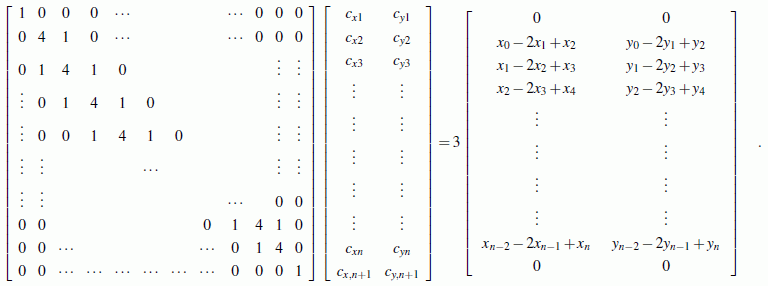
Danach ergeben sich die restlichen Ansatzkoeffizienten nach folgenden Formeln:
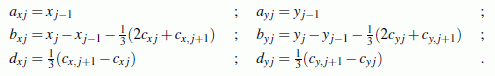

Beispiel: Der beschriebene Algorithmus ist in dem Programm "Splines" (zu finden unter TM-interaktiv) realisiert. Für das auf der Seite "Natürliche Splines" demonstrierte Beispiel mit 5 Stützpunkten liefert es die nebenstehend zu sehenden Parameterdarstellungen der 4 Spline-Funktionen.
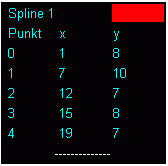

Links sieht man die von dem Programm ausgegebene Tabelle der Koordinaten der Stützpunkte, rechts die grafische Darstellung der Spline-Kurve.
Berechnung der Spline-Funktionen für geschlossene und periodische Splines
Für geschlossene und periodische Splines weichen zwei Bedingungen für die Berechnung der Koeffizienten der Ansatzfunktionen von den Bedingungen für offene Splines ab (siehe die Liste der Bedingungen auf der Seite "Natürliche Splines"): Die ersten beiden Ableitungen an Anfangs- und Endpunkt der Splinekurven müssen gleich sein (bei geschlossenen Splines auch die Punktkoordinaten, aber das ist natürlich automatisch erfüllt).
Auch hierfür wird der komplette Algorithmus unter Berücksichtigung der oben beschriebenen Vereinfachungen zusammengestellt. Zunächst müssen die cxj und cyj aus folgendem Gleichungssystem berechnet werden:
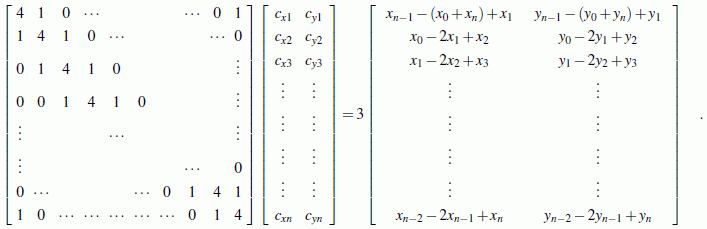
Danach ergeben sich die restlichen Ansatzkoeffizienten nach folgenden Formeln:
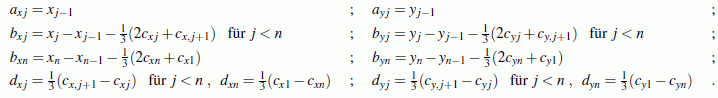
Beispiel für einen geschlossenen Spline
| j | 0 | 1 | 2 | 3 |
| xj | 0 | 3 | 6 | 0 |
| yj | 0 | 4 | 0 | 0 |
Die 3 Punkte P0, P1 und P2 sollen mit einem geschlossenen Spline verbunden werden. Zunächst wird ein vierter Punkt P3 mit den gleichen Koordinaten wie Punkt P0 hinzugefügt. Die nebenstehende Tabelle zeigt die Koordinaten der Punkte, für die die 3 Splinekurven berechnet werden sollen.
Das Gleichungssystem für die Berechnung der cxj und cyj kann mit den gegebenen Koordinaten sofort formuliert werden. Für die Lösung bietet sich das Programm "Cholesky-Verfahren" an (zu finden unter TM-interaktiv). Nachfolgend sieht man Bildschirm-Schnappschüsse von der Lösung mit diesem Programm:

Damit können nun alle Koeffizienten für die Spline-Funktionen berechnet werden:
| j | xj | yj | cxj | cyj | axj | ayj | bxj | byj | dxj | dyj |
| 0 | 0 | 0 | ||||||||
| 1 | 3 | 4 | 9 | 4 | 0 | 0 | −3 | 4 | −3 | −4 |
| 2 | 6 | 0 | 0 | −8 | 3 | 4 | 6 | 0 | −3 | 4 |
| 3 | 0 | 0 | −9 | 4 | 6 | 0 | −3 | −4 | 6 | 0 |
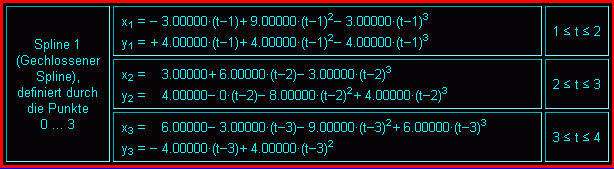
Natürlich ist diese etwas mühsame Handrechnung nicht erforderlich, denn der beschriebene Algorithmus ist auch in dem Programm "Splines" (zu finden unter TM-interaktiv) realisiert. Für dieses Beispiel liefert es die nebenstehend zu sehenden Parameterdarstellungen der 3 Spline-Funktionen. Man erkennt die Koeffizienten, die in der Tabelle verzeichnet sind.
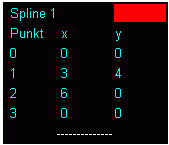
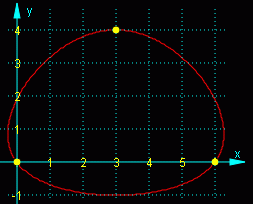
Links sieht man die von dem Programm ausgegebene Tabelle der Koordinaten der Stützpunkte, rechts die grafische Darstellung der Spline-Kurve.

