Nullstellen-Berechnung

Aufgabe

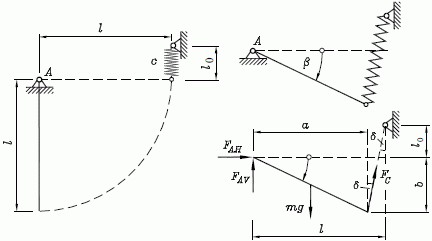
Im Kapitel "Elastische Lager" des Buchs "Dankert/Dankert: Technische Mechanik" wird die nebenstehend skizzierte Aufgabe behandelt: Ein Stab (Masse m, Länge l) wird in eine Feder (Federzahl c, Länge der entspannten Feder l₀) eingehängt. Gefragt wird nach den möglichen Gleichgewichtslagen, die durch den Winkel β beschrieben werden sollen. Für die physikalischen Eigenschaften von Stab und Feder sollen die Werte cl/(mg) = 1 bzw. l₀/l = 1 angenommen werden.

Die Gleichgewichtsbedingung (Summe aller Momente um das Lager) führt auf die Funktion

deren Nullstellen die gesuchten Gleichgewichtslagen beschreiben.

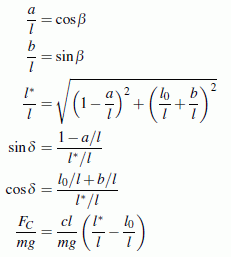
Es sieht natürlich nur so aus, als würde in f(β) die Variable β gar nicht vorkommen. Sie steckt in den geometrischen Beziehungen, die nebenstehend zusammengestellt sind.

Man könnte diese Beziehungen nun in f(β) einsetzen, so dass diese Funktion neben β nur noch die gegebenen Größen enthält. Das ist aber mühsam und fehlerträchtig. Deshalb werden alle Beziehungen als Funktionensatz aufgefasst, wobei auf die Reihenfolge geachtet werden muss: Jede Funktion darf neben den gegebenen Größen und der Variablen β nur vorab definierte Funktionen enthalten.

Die geometrischen Beziehungen sind schon in diesem Sinne geordnet und müssen nur durch f(β) als letzte Funktion ergänzt werden. Die Nullstellen werden nachfolgend mit dem Programm "Funktionen analysieren" (zu finden unter "TM-interaktiv") berechnet. Als Funktionsbezeichner werden "sprechende Namen" eingeführt: adl ("a durch l"), bdl ("b durch l"), lsdl ("l-Stern durch l"), sd ("Sinus delta"), cd ("Cosinus delta"), Fcdmg ("F_C durch mg").

Zunächst werden die beiden gegebenen Größen als Konstanten cldmg = 1 ("cl durch mg") bzw. l0dl = 1 ("l₀ durch l") definiert. Die unabhängige Variable wird in beta geändert, danach werden die Funktionen in der oben genannten Reihenfolge (beginnend mit adl, endend mit f) eingegeben.

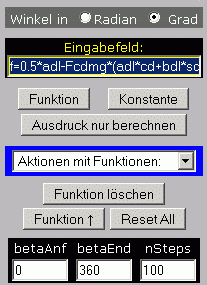
Weil mit β = 0°...360° der gesamte interessierende Bereich erfasst wird, ändert man betaAnf auf 0 und betaEnd auf 360 und muss, wenn in Grad gerechnet werden soll, oben links auch noch von Radian auf Grad umstellen.

Weil nur die Ergebnisse für die Funktion f interessieren, sollte man alle "Häkchen" vor den anderen Funktionen entfernen, um nicht auch für alle diese Funktionen die Nullstellensuche durchführen zu lassen. Schließlich wählt man unter "Aktionen mit Funktionen" vorsichtshalber "Grafik, spezielle Punkte" aus (natürlich würde für diese Aufgabe auch die Auswahl "Nullstellen" genügen).

Der Bildschirm müsste danach folgendermaßen aussehen:

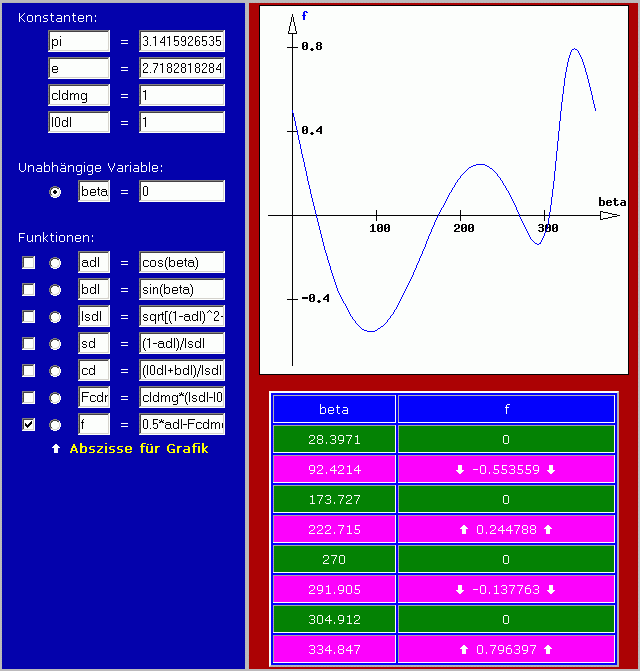
Für Interessenten: Es gibt tatsächlich vier mögliche Gleichgewichtslagen, von denen allerdings nur zwei stabil sind. Die kleinen Bildchen unten zeigen symbolisch die Gleichgewichtslagen: Stabil sind nur die Lagen β₀₁ und β₀₃. Man kann sich gut vorstellen, dass die stark gedehnte bzw. stark zusammengedrückte Feder bei den beiden anderen Gleichgewichtslagen dafür sorgt, dass die geringste Abweichung von dieser Lage sofort zum Übergang in eine der stabilen Lagen führt.

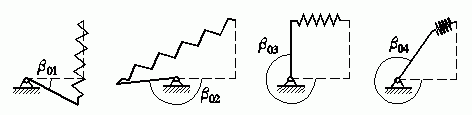
Die Lösung dieser Aufgabe nach der Strategie "Funktionensatz" findet über die Seite "Gleichgewicht bei einer weichen Feder" auch unter Verwendung der Mathematik-Programme Matlab und Maple.