Bézier-Splines
Für die Darstellung beliebiger Funktionen, die durch eine Punktmenge definiert werden, hat sich in CAD-Systemen (auch in der NC-Programmierung) eine auf den französischen Ingenieur Pierre Bézier zurückgehende Idee durchgesetzt, der für die Karosseriekonstruktion bei der Firma Renault am Anfang der 70er Jahre des vorigen Jahrhunderts spezielle Spline-Kurven verwendete, die im Gegensatz zur Interpolation mit natürlichen Splines nicht alle Stützstellen treffen (deshalb werden für die Punkte oft auch die Ausdrücke "Kontroll"-, "Leit"- oder "Steuer"-Punkte verwendet, hier wird weiter von Stützstellen gesprochen).
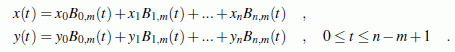
- Die Anzahl der Basispolynome Bi,m ist also von der Anzahl der Stützstellen abhängig. Das bedeutet, dass eine Vorschrift existieren muss, nach der die Basispolynome erzeugt werden.
- Der Index m kennzeichnet den Grad der Basispolynome.
- Man beachte, daß bei vorgegebenen Basispolynomen keine Ansatzparameter auszurechnen sind (wie bei der Arbeit mit natürlichen Splines), die Approximationsfunktionen werden "einfach aufgeschrieben".
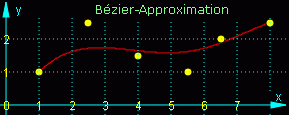
Die Bézier-Approximationen unterscheiden sich im Wesentlichen in der Definition der Basispolynome. Gebräuchlich sind die so genannten "Bernsteinpolynome" (behandelt auf der Seite "Bézier-Bernstein-Approximation") und die "B-Spline-Funktionen" (behandelt auf der Seite "Bézier-B-Spline-Approximation").
Nebenstehend sieht man die Approximation einer Punktmenge als Bézier-Spline unter Verwendung von Bernsteinpolynomen.
Stützpolygon, allgemeine Eigenschaften der Bézier-Approximation
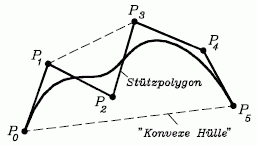
Für die Bézier-Approximationen gelten allgemein folgende Eigenschaften, die sich zum Teil auf das sogenannte "Stützpolygon" (Polygonzug durch alle Stützpunkte) beziehen (das nebenstehende Bild zeigt ein Beispiel mit n = 5):
- Die Bézier-Kurve hat mit dem Stützpolygon den Anfangspunkt (x0,y0) und den Endpunkt (xn,yn) gemeinsam. Die übrigen Punkte beeinflussen den Verlauf (üben eine "Anziehungskraft" auf die Kurve aus).
- Die Richtung der Tangente der Bézier-Kurve im Punkt (x0,y0) stimmt mit der Richtung des 1. Segments des Stützpolygons (Segment zwischen den Punkten P0 und P1), im Punkt (xn,yn) mit der Richtung des letzten Segments des Stützpolygons überein.
- Die Bézier-Kurve liegt vollständig innerhalb der konvexen Hülle der Stützpunkte ("Konvexe Hülle": Man denke sich ein Gummiband um sämtliche Stützpunkte gelegt).

