Definitionen
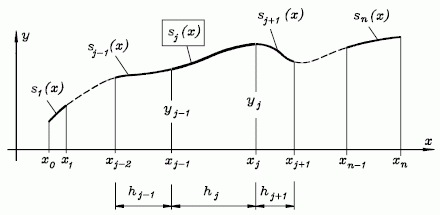
Gegeben seien n+1 Punkte, die auf "natürliche Weise" durch Interpolationsfunktionen miteinander verbunden werden sollen. Um diesen Begriff mathematisch umsetzen zu können, dient folgende Modellvorstellung: Ein elastisches Lineal (engl.: "SPLINE" - biegsame Feder, Latte) wird so verformt, dass es durch die n+1 Punkte verläuft. Es ergibt sich eine Kurve (beschreibbar durch n Funktionen in n Bereichen, nebenstehende Skizze), für die nach den Regeln der Technischen Mechanik folgende Aussagen möglich sind:
- Da die Belastung nur an den Stützstellen eingeleitet wird, wird die "Biegelinie" in jedem der n Bereiche durch eine Polynomfunktion dritten Grades beschrieben (gilt eigentlich nur für "kleine Verformungen", wird hier jedoch allgemein verwendet), so daß 4n Koeffizienten zu bestimmen sind, die sämtliche Funktionen beschreiben.
- Jedes (jeweils nur in einem Bereich gültige) Polynom muß die beiden "Verschiebungsrandbedingungen" an beiden Rändern erfüllen (2n Bedingungen).
- Benachbarte Polynome stoßen an den Übergangsstellen tangential aneinander (n−1 "Übergangsbedingungen").
- Die Gleichheit der Biegemomente an den Übergangsstellen wird durch Gleichheit der zweiten Ableitungen der jeweils beiden Polynome an diesen Punkten garantiert (n−1 "Übergangsbedingungen").
- Für die Endpunkte muss zwischen drei Möglichkeiten unterschieden
werden:
- Bei den so genannten "Offenen Splines" (Bild oben rechts) gilt die Modellvorstellung, dass an den beiden freien Rändern das Biegemoment (und damit die zweite Ableitung) gleich Null ist (2 Bedingungen). Nachfolgend wird diese Variante behandelt.
 Bei den so genannten "Periodischen Splines" wird angenommen,
dass sich die Kurve nach rechts und/oder links
periodisch fortsetzt, so dass Anfangs- und Endpunkte
gleiche Eigenschaften haben sollten. In diesem Fall gilt,
dass an Punkt 0 und Punkt n
die erste und die zweite Ableitung gleich sind.
Bei den so genannten "Periodischen Splines" wird angenommen,
dass sich die Kurve nach rechts und/oder links
periodisch fortsetzt, so dass Anfangs- und Endpunkte
gleiche Eigenschaften haben sollten. In diesem Fall gilt,
dass an Punkt 0 und Punkt n
die erste und die zweite Ableitung gleich sind.
- Bei den so genannten "Geschlossenen Splines" sind Anfangs- und Endpunkt identisch. Die Bedingungen für diese beiden Punkte entsprechen denen der periodischen Splines. Die Variante "Geschlossener Spline" ist nur mit Splinefunktionen in Parameterdarstellung möglich.
Funktionen, die auf die beschriebene Weise die Stützstellen miteinander verbinden, heißen natürliche Splines. Sie haben wie die Polynom-Interpolation den Vorteil, alle Stützstellen zu "treffen", vermeiden aber den wesentlichen Nachteil der Polynom-Interpolation, zwischen den Stützstellen sehr weit auszuschwingen.
Während sich bei der Polynom-Interpolation stets eindeutige Funktionen ergeben (zu jedem x-Wert gehört genau ein y-Wert), können mit der Spline-Interpolation (unter Verwendung der Parameterdarstellung) beliebige (auch sich mehrfach selbst schneidende und geschlossene) Kurven nachgebildet werden. Man beachte, dass bei der Definition der Punktmenge, die die Kurve beschreibt, die Reihenfolge der Punkte bei der Spline-Interpolation (im Gegensatz zur Polynom-Interpolation) eine Rolle spielt.
Berechnung der Spline-Funktionen (offene Splines)
Für jeden Abschnitt j = 1, ... , n (siehe Skizze oben rechts) wird ein Polynomansatz
![]()
mit den unbekannten Parametern aj, bj, cj und dj, gewählt (xj−1 ist die Abszisse des linken Randpunktes des Abschnitts j). Nachfolgend sind die Formeln zusammengestellt, mit denen diese insgesamt 4n Parameter berechnet werden können (die ausführliche Herleitung der Formeln findet man in dem PDF-Skript "Interpolations- und Ausgleichsfunktionen").
Mit den Abschnittsbreiten hj und den damit zu berechnenden Hilfsgrößen gj entsprechend
![]()
kann das folgende lineare Gleichungssystem formuliert werden:
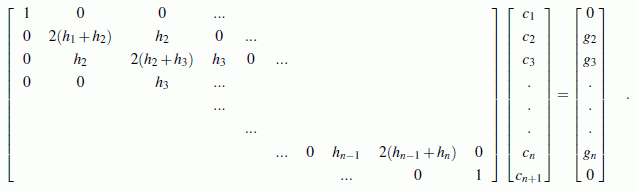
Die Lösung dieses Gleichungssystems liefert die cj-Werte, mit denen die übrigen Parameter der Spline-Funktionen nach folgenden Formeln bestimmt werden können:
![]()
Hinweis: Das Gleichungssystem für die Berechnung der cj-Werte hat eine symmetrische und bandförmige Koeffizientenmatrix (Tridiagonalmatrix). Da die hj-Werte für den hier betrachteten Fall garantiert positiv sein müssen, ist die Matrix positiv definit, und für die Lösung des Gleichungssystems kann das effektiv arbeitende Cholesky-Verfahren verwendet werden. Diese Einschränkung für die hj-Werte gilt nicht bei Arbeit mit Ansatzfunktionen in Parameterdarstellung.
Beispiel
| j | 0 | 1 | 2 | 3 | 4 |
| xj | 1 | 7 | 12 | 15 | 19 |
| yj | 8 | 10 | 7 | 8 | 7 |
Es sind 5 Punkte entsprechend nebenstehender Wertetabelle gegeben. Sie sollen durch eine Spline-Interpolation verbunden werden. Diese soll verglichen werden mit der Polynominterpolation (Polynom 4. Grades für 5 Punkte).
Zunächst werden die hj- und gj-Werte nach den oben angegebenen Formeln berechnet (sind in der Tabelle unten zusammengestellt), mit denen das lineare Gleichungssystem formuliert werden kann. Nachfolgend sieht man den Bildschirm-Schnappschuss des Programms "Lineares Gleichungssystem, Matrixinversion" (zu finden unter TM-interaktiv), links das Gleichungssystem, rechts das Ergebnis:
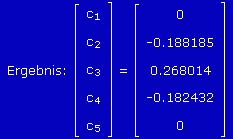

Damit können nun alle Parameter für die 4 Spline-Funktionen berechnet werden:
| j | xj | yj | hj | gj | cj | aj | bj | dj |
| 0 | 1 | 8 | ||||||
| 1 | 7 | 10 | 6 | 0 | 8 | 0,7097 | −0,01045 | |
| 2 | 12 | 7 | 5 | −2,8 | −0,188185 | 10 | −0,4194 | 0,03041 |
| 3 | 15 | 8 | 3 | 2,8 | 0,268014 | 7 | −0,02026 | −0,05005 |
| 4 | 19 | 7 | 4 | −1,75 | −0,182432 | 8 | 0,2365 | 0,01520 |
| 0 |
Damit können die vier Spline-Funktionen formuliert werden:
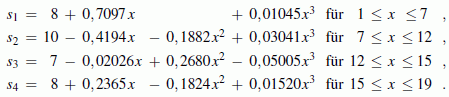
Die nebenstehende Grafik zeigt die Spline-Funktionen als rote Kurve. Zum Vergleich wurde als blaue Kurve die Polynomfunktion 4. Grades eingezeichnet, die sich mit den 5 Stützstellen berechnen lässt:
![]()
Man erkennt, dass die Spline-Funktionen wie die Polynomfunktion 4. Grades alle Stützstellen treffen, dass aber das weite Ausschwingen nach oben bzw. unten von den Spline-Funktionen vermieden wird.
Das unter TM-interaktiv verfügbare Programm "Splines" gestattet die bequeme Berechnung von Splines aller oben genannten Typen auf dieser Basis.

