Regel von de l'Hospital: Betrachtet werden Funktionen der Form
![]()
für die für eine bestimmte Stelle x0
![]()
gilt. Unter diesen Voraussetzungen (Ausdrücke der Form "0/0" oder "∞/∞") darf die so genannte "de l'Hospitalsche Regel" angewendet werden (gilt auch für x0 = ±∞):
![]()
- Man beachte, dass Zähler und Nenner jeweils für sich abgeleitet werden müssen. Es entsteht ein neues Grenzwertproblem, von dem man hoffen darf (mehr nicht!), dass es einfacher zu lösen ist.
- Natürlich kann man hartnäckig bleiben und die "de l'Hospitalsche Regel" mehrfach anwenden, bis sich schließlich (ohne Garantie) ein lösbares Grenzwertproblem ergibt.
- Mit einigen kleinen Tricks (siehe nachfolgende Beispiele, die eine Anpassung erfordern) können neben den Varianten "0/0" oder "∞/∞" (nur dafür gilt die "de l'Hospitalsche Regel") auch Grenzwerte für Ausdrücke der Form "0·∞", "1∞", "00" und "∞−∞" behandelt werden.
Beispiel 1: Die Berechnung des Funktionswertes an der Stelle x = 0 für die Funktion
![]()
scheitert am Problem "0/0". Der Grenzwert kann mit der "de l'Hospitalschen Regel" gefunden werden:
![]()
Beispiel 2: Die folgende Grenzwertberechnung für ein Problem der Form "∞/∞" gelingt nach zweifacher Anwendung der "de l'Hospitalschen Regel":
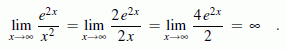
Ein typisches Beispiel eines Problems mit Praxisbezug, das durch mehrfache Anwendung der "de l'Hospitalschen Regel" gelöst wird, findet man auf der Seite "Grenzwerte, Regel von de l'Hospital, Beispiel Biegefeder".
Beispiele, die eine Anpassung erfordern
Beispiel 3: Die Berechnung des Funktionswertes an der Stelle x = 0 für die Funktion
![]()
scheitert am Problem "0·∞". Nach einer identischen Umformung entsprechend
![]()
entsteht ein Problem der Form "∞/∞", so dass der Grenzwert mit der "de l'Hospitalschen Regel" gefunden werden kann:
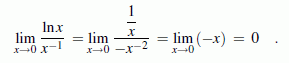
Beispiel 4: Die Berechnung des Funktionswertes an der Stelle x = 0 für die Funktion
![]()
scheitert am Problem "00". Nach einer identischen Umformung (generell gilt die identische Umformung a = eln a) entsprechend
![]()
entsteht folgendes Problem:
![]()
wobei für den Exponenten der im Beispiel 3 berechnete Grenzwert verwendet wurde.
Beispiel 5: Die Berechnung des Grenzwertes
![]()
ist ein Problem der Form "1∞". Nach einer identischen Umformung (generell gilt die identische Umformung a = eln a) entsprechend
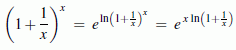
muss der Grenzwert für den Exponenten bestimmt werden. Dieser hat die Form "∞·0" und muss also selbst noch einmal umgeformt werden:
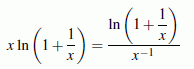
ist vom Typ "0/0" und kann mit der "de l'Hospitalschen Regel" behandelt werden:
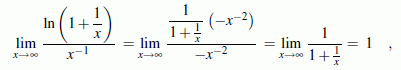
und dieses Ergebnis wird in das Ausgangsproblem eingesetzt:
![]()

