Nullstellen-Berechnung

Aufgabe

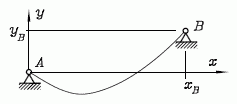
Im Kapitel "Seilstatik, Kettenlinien, Stützlinien" des Buchs "Dankert/Dankert: Technische Mechanik" wird gezeigt, dass für die Berechnung der Seilline unter Eigengewicht (nebenstehende Skizze, gegeben: x_B = 0,8; y_B = 0,2) zunächst der so genannte "Horizontalzug" F_SH ermittelt werden muss, der sich als Nullstelle der Funktion

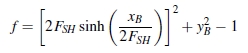
ergibt (hier findet man die komplette Rechnung für diese Aufgabe). Diese Nullstelle, die aus physikalischen Gründen nur positiv sein kann, wird nachfolgend mit dem Programm "Funktionen analysieren" (zu finden unter "TM-interaktiv") berechnet. Nachdem zunächst die beiden Konstanten xB = 0.8 und yB = 0.2 definiert wurden und die unabhängige Variable in FSH umbenannt und ihr Wert auf FSH = 1 geändert wurde (weil der Syntaxcheck bei der Eingabe der Funktion wegen der Division durch FSH einen Fehler melden würde), wurde die Funktion definiert. Weil nur positive Ergebnisse sinnvoll sind, wurde die Untergrenze des zu untersuchenden Bereichs auf FSHanf = 0 geändert.

Der linke Teil des Bildschirms sieht dann wie folgt aus, und aus dem Angebot "Aktionen mit Funktionen" wird "Grafik, spezielle Punkte" gewählt:

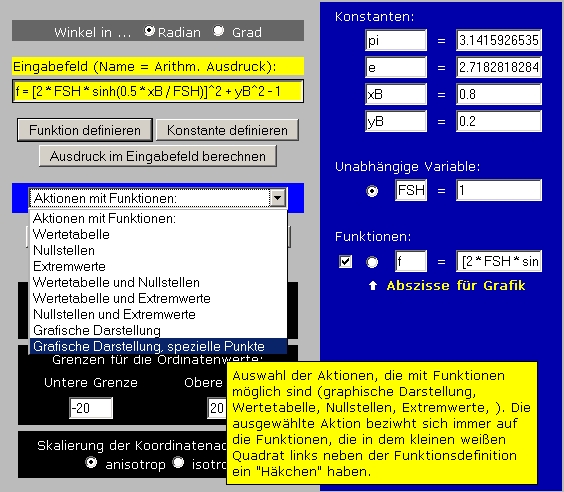
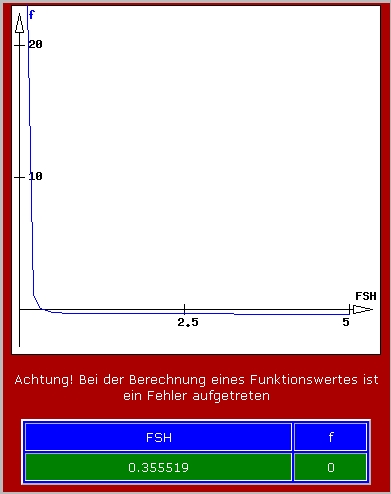
Nebenstehend sieht man das Ergebnis. Die Grafik zeigt, dass es nur eine Nullstelle gibt (vorsichtshalber könnte man noch eine Grafik über einen erweiterten Bereich anfordern). Die Tabelle unten zeigt, dass es nur einen speziellen Punkt im untersuchten Bereich gibt, die gesuchte Nullstelle.

Die Ausschrift "Achtung! Bei der Berechnung eines Funktionswertes ist ein Fehler aufgetreten" weist auf die Polstelle bei x = 0 hin.

Auf der Seite mit der kompletten Rechnung für diese Aufgabe einschließlich der Berechnung und grafischen Darstellung der Seilkurve wird gezeigt, wie die Suche der Nullstelle für die Funktion f mit dem Mathematikprogramm Maple realisiert wird.