B-Spline-Basisfunktionen
Mit den sogenannten "B-Splines" als Basisfunktionen der Bézier-Approximation gelingt es, alle Vorteile der Bézier-Bernstein-Approximation bei Ausschaltung der Mängel zu erhalten. Insbesondere gelingt die Entkopplung des Grades m der Polynomfunktionen von der Anzahl der Stützstellen n + 1 (in dieser Hinsicht besteht eine Verwandtschaft mit den natürlichen Splines). Man bezahlt die Vorteile mit einem höheren Aufwand bei der Berechnung der Funktionswerte für die Basisfunktionen, deren rekursive Definition etwas kompliziert aussieht, was den Anwender, der die Auswertung der Formeln einem Programm überträgt, aber nicht berührt.
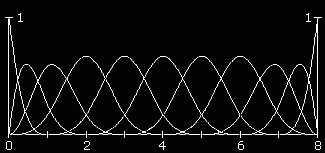 B-Spline-Basisfunktionen für n = 10 und m = 3 liegen im Bereich 0 ≤ t ≤ 8. |
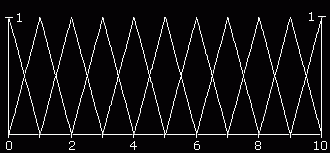 B-Spline-Basisfunktionen für n = 10 und m = 1 liegen im Bereich 0 ≤ t ≤ 10. |
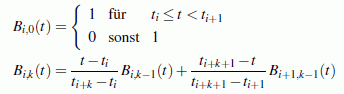
Da diese Basisfunktionen für alle Stützstellen i = 0, 1, ..., n berechnet werden müssen, nehmen die Indizes der tj die Werte j = 0, 1, ..., n + m + 1 an. Die tj werden wie folgt berechnet:
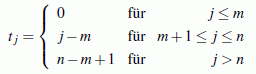
Bei der rekursiven Berechnung der Bi,k können Ausdrücke der Form "0/0" auftreten, für die jeweils der Wert 0 angenommen werden muss.
Die beiden Beispiele rechts verdeutlichen, dass die B-Spline-Basisfunktionen nur in relativ schmalen Bereichen von Null verschieden sind. Deshalb wirken sich Veränderungen der Stützstellen auch nur in einem begrenzten Bereich aus. Je kleiner der Grad m der Ansatzfunktionen ist, desto schmaler ist dieser Bereich. Damit unterscheiden sie sich von den Bernstein-Polynomen, die (bis auf eine Nullstelle) im gesamten Definitionsbereich von Null verschieden sind.
Gemeinsam mit den Bernstein-Polynomen haben die B-Spline-Basisfunktionen die Eigenschaft, für i = 0 und i = n an den Rändern den Wert 1 anzunehmen, während alle übrigen Polynome an beiden Rändern verschwinden.
Strategie der Berechnung einer Bézier-B-Spline-Approximation
Die Berechnung einer Bézier-B-Spline-Approximation kann nur punktweise erfolgen. Dies sind die erforderlichen Schritte:
- Gegeben sind n + 1 Punkte (x0,y0), (x1,y1), ... , (xn,yn). Unabhängig von der Anzahl der Punkte wird der Grad m der B-Spline-Basisfunktionen festgelegt.
- Die Bézier-B-Spline-Approximation kann nur punktweise ermittelt
werden. Die Punktkoordinaten werden nach
berechnet, wobei der Parameter t den angegebenen Bereich, der durch n und m festgelegt wird, überstreichen muss.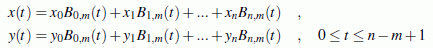
- Die Berechnung eines (x,y)-Wertepaares für einen Wert von t erfordert jeweils die komplette Abarbeitung der oben angegebenen rekursiven Vorschrift zur Berechnung der Bi,k(t).
Diese Strategie ist (neben der Möglichkeit, natürliche Splines und Bézier-Bernstein-Splines zu berechnen) im interaktiv zu nutzenden Progamm "Splines" realisiert. Die nachfolgend zu sehenden Beispiele wurden mit diesem Programm berechnet.
Demonstration der Eigenschaften von Bézier-B-Spline-Approximationen
 Bézier-B-Spline-Approximation für n = 6 und m = 3 mit Stützpolygon |
Die wichtigsten Eigenschaften der Bézier-B-Spline-Approximationen werden nachfolgend zusammengestellt und jeweils an Beispielen demonstriert:
- Alle für die Bézier-Bernstein-Approximationen aufgelisteten Eigenschaften gelten auch für die Bézier-B-Spline-Approximationen: Anfangs- und Endpunkte sind mit den Anfangs- und Endpunkten des Stützpolygons identisch, Tangentenrichtungen in diesen Punkten stimmen mit den Tangentenrichtungen des Stützpolygons überein (siehe nebenstehendes Beispiel), Kurve liegt vollständig innerhalb der "konvexen Hülle" der Stützpunkte.
- Für m = 1 (lineare B-Spline-Basis-Polynome) ist die Bézier-B-Spline-Approximation mit dem Stützpolygon identisch.
- Für m = n (Grad der B-Spline-Basispolynome ist um 1 kleiner als die Anzahl der Stützstellen und entspricht damit dem Grad der Bernstein-Polynome) ist die Bézier-B-Spline-Approximation mit der Bézier-Bernstein-Approximation identisch.
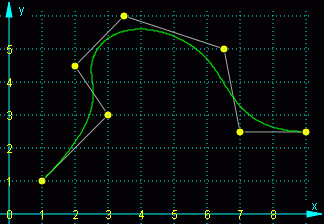
 Bézier-B-Spline-Approximationen mit m = 3 (gelbe Kurve) und m = 6 (grüne Kurve) |
- Je niedriger der Grad der B-Spline-Basisfunktionen ist, desto besser ist die Anpassung der Bézier-B-Spline-Approximation an das Sützpolygon (man vergleiche die nebenstehend zu sehenden Kurven). Deshalb werden besonders gern Basisfunktionen mit m = 2 oder m = 3 verwendet.
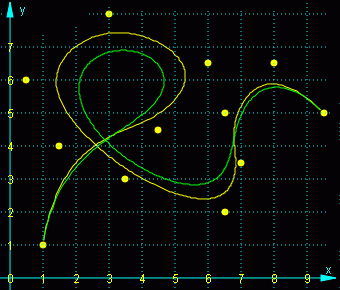
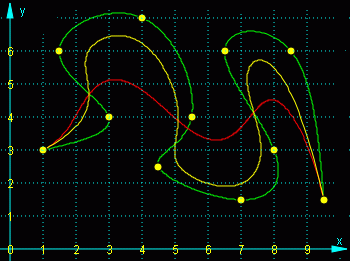 Natürlicher Spline (grüne Kurve), Bézier-B-Spline-Approximationen mit m = 3 (gelbe Kurve) und Bézier-Bernstein-Approximation (rote Kurve) |
- Bézier-B-Spline-Approximationen passen sich besser an den
Stützpolygonzug an als die Bézier-Bernstein-Approximationen
(Ausnahme ist der Fall
m = n, für den
die beiden Approximationen identisch sind).
Nebenstehend sieht man ein Beispiel, bei dem zum Vergleich auch die natürliche Spline-Kurve gezeichnet wurde, die per Definition durch alle Stützpunkte verläuft.
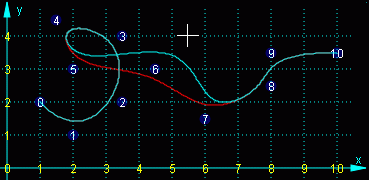 Verschiebung eines einzelnen Punktes |
- Da die B-Spline-Basispolynome nur in einem (bei kleinem m sehr schmalen) Bereich von Null verschieden sind, können die Bézier-B-Spline-Approximationen lokal kontrolliert werden: Die Änderung eines Punktes hat im allgemeinen nur Auswirkungen auf die Bereiche in der Nähe dieses Punktes (genau auf m + 1 Bereiche, bei m = 3 z. B. auf jeweils zwei Bereiche links bzw. rechts vom geänderten Punkt). Der nebenstehende Bildschirm-Schnappschuß zeigt die Auswirkung der Verschiebung des Punktes 6, (das weiße Cursor-Kreuz zeigt die aktuelle Position des Punktes während der Verschiebung). Die aktuelle (hellblaue) Kurve unterscheidet sich nach links nur bis zum Punkt 4, nach rechts bis zum Punkt 8.
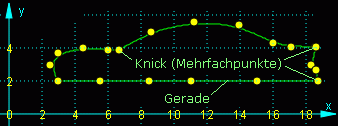 Knickstellen und Geradenstück |
- Wenn mindestens m + 1 Punkte des Stützpolygons auf einer Geraden liegen, dann ist auch die Bézier-B-Spline-Approximation in diesem Bereich eine Gerade (es können exakt linear verlaufende Teilstücke realisiert werden, nebenstehendes Beispiel).
- Es ist möglich, in der Punktfolge zwei oder mehr identische Punkte (unmittelbar aufeinander folgend) zu haben, die dann eine entsprechend "vergrößerte Anziehungskraft" auf die Kurve ausüben. Bei m + 1 (oder mehr) identischen Punkten verläuft die Kurve durch diese Punkte. Da die Kurve an solchen Stellen eine theoretisch unendlich große Krümmung realisieren kann, hat man damit auch die Möglichkeit, einen "Knick" in den Kurvenverlauf einzufügen.

