Bernstein-Polynome
Die Bézier-Approximation einer geordneten Menge von n + 1 Punkten (x0,y0), (x1,y1), ... , (xn,yn) erfolgt mit folgender in Parameterdarstellung definierten Funktion (vgl. Seite "Bézier-Approximationen"):
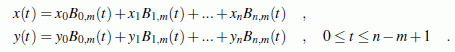
Eine beliebte Vorschrift zur Definition der Basispolynome Bi,m ist die Festlegung, dass der Grad der Polynome m = n ist (Grad der Approximationspolynome ist um 1 kleiner als die Anzahl der Stützstellen) und die nach dem russischen Mathematiker Sergej Bernstein benannten Funktionen verwendet werden, die so genannten
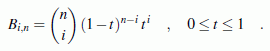
Die Approximation erfolgt also mit n + 1 Basispolynomen n-ten Grades (i = 0 ... n).
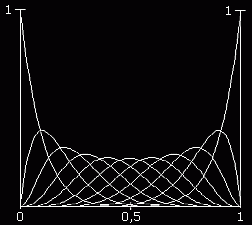
Rechts sieht man als Beispiel die 11 Bernstein-Basispolynome für n = 10. Man erkennt eine typische Eigenschaft der Bernstein-Polynome: Die beiden Polynome für i = 0 und i = n nehmen an den Rändern den Wert 1 an, alle übrigen Bernstein-Polynome verschwinden an beiden Rändern (dies ist der Grund für die erste der nachfolgend formulierten Eigenschaften der Bézier-Bernstein-Approximationen).
Stützpolygon, allgemeine Eigenschaften der Bézier-Bernstein-Approximation
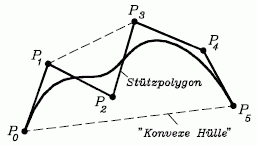
Für die Bézier-Approximationen gelten allgemein folgende Eigenschaften, die sich zum Teil auf das sogenannte "Stützpolygon" (Polygonzug durch alle Stützpunkte) beziehen (das nebenstehende Bild zeigt ein Beispiel mit n = 5):
- Die Bézier-Kurve hat mit dem Stützpolygon den Anfangspunkt (x0,y0) und den Endpunkt (xn,yn) gemeinsam. Die übrigen Punkte beeinflussen den Verlauf (üben eine "Anziehungskraft" auf die Kurve aus).
- Die Richtung der Tangente der Bézier-Kurve im Punkt (x0,y0) stimmt mit der Richtung des 1. Segments des Stützpolygons (Segment zwischen den Punkten P0 und P1), im Punkt (xn,yn) mit der Richtung des letzten Segments des Stützpolygons überein.
- Die Bézier-Kurve liegt vollständig innerhalb der konvexen Hülle der Stützpunkte ("Konvexe Hülle": Man denke sich ein Gummiband um sämtliche Stützpunkte gelegt).
Einfaches Beispiel

Für 4 Punkte (x0,y0), (x1,y1), (x2,y2) und (x3,y3) entsprechend nebenstehender Wertetabelle soll die Bézier-Bernstein-Approximation erzeugt werden.
Für n + 1 = 4 sind die 4 Bézier-Basispolynome vom Grad m = n = 3. Nach der oben angegebenen Formel sind es diese:
![]()
Der Ansatz mit diesen 4 Funktionen sieht so aus:
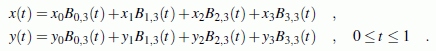
Einsetzen der gegebenen Punkte und der Basispolynome liefert die Parameterdarsellung der Bézier-Bernstein-Approximation:
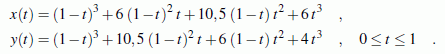
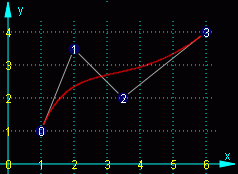
Nebenstehend sieht man die grafische Darstellung des Splines gemeinsam mit dem Stützpolygon. In diesem Fall mit m = n = 3 (allerdings nur in diesem Fall) kann die entstehende Spline-Kurve sehr schön mechanisch gedeutet werden:
Man stelle sich eine elastische Biegefeder ("Spline") vor, deren Endpunkte mit den Punkten P0 und P3 zusammenfallen. An den Endpunkten sind parallel zur Biegefeder zwei starre Hebel angeschweißt (in der Grafik die Linien 0-1 und 2-3). Diese werden nun (durch Drehung um P0 bzw. P3) auf die Verbindungslinien von P0 und P1 bzw. P3 und P2 ausgerichtet. Dann nimmt die Biegefeder die Form der Bézier-Bernstein-Kurve an (unbelasteter Biegeträger, dem an den Endpunkten vorgeschriebene Biegewinkel aufgezwungen werden).
Stärken und Schwächen der Bézier-Bernstein-Approximation
Der erhebliche Vorteil, dass die Bézier-Bernstein-Approximationen einfach mit den Stützstellen-Koordinaten unter Verwendung problemlos zu erzeugender Basisfunktionen aufgeschrieben werden können (es müssen keine Ansatzparameter berechnet werden), bedeutet natürlich auch, dass für eine weitere Funktion ein selbstständiger Ausdruck formuliert wird, der keinerlei Verknüpfungen (wie bei den natürlichen Splines) mit seinem Vorgänger hat.
Dass der Grad der Bézier-Bernstein-Polynome an die Anzahl der Stützstellen gekoppelt ist, bedeutet bei wachsender Anzahl der Stützstellen, dass immer höhergradigere Polynome erzeugt werden. Dies führt dazu, dass die Approximationsfunktionen erheblich vom Stützpolygon abweichen. Der Einfluß des einzelnen Punktes auf den Verlauf lässt dann nach, obwohl jede Koordinatenänderung den gesamten Verlauf der Funktion ändert.
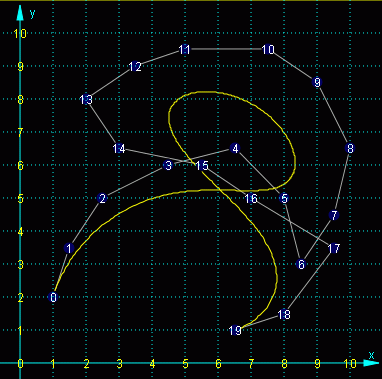
Dies kann sehr schön mit dem Programm "Splines" demonstriert werden, dass unter "TM-interaktiv" zu finden ist. Nebenstehend sieht man eine Bézier-Bernstein-Kurve, die mit diesem Programm erzeugt wurde. Man erkennt, dass die auf dem Stützpolygon liegenden Punkte tatsächlich nur eine gewisse "Anziehungskraft" auf die Kurve ausüben. Weil eine Kurve auch nachträglich durch Verschieben einzelner Punkte ("Drag and Drop") verändert werden kann, lässt sich der Einfluss des einzelnen Punktes sehr schön verfolgen.
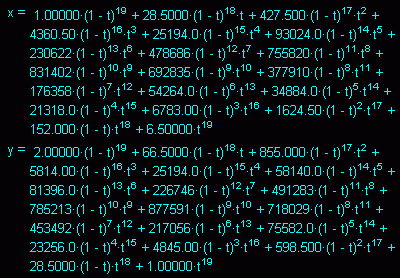
Das Programm "Splines" liefert auch die analytische Darstellung der erzeugten Kurve (in Parameterdarstellung). Nebenstehend sieht man die zur Grafik gehörende Funktion 19. Grades. Solche Funktionen sind aus numerischer Sicht extrem kritisch und können durchaus zu instabilem Verhalten bei Änderungen führen. Allerdings verkraftet das Programm "Splines" auch noch Funktionen wesentlich höheren Grades.
Abhilfe kann die gleiche Strategie schaffen, die bei den natürlichen Splines verfolgt wurde: Es werden abschnittsweise Bézier-Bernstein-Polynome niedriger Ordnung verwendet, die an den Nahtstellen auf geeignete Weise verbunden werden müssen. Interaktiv können zwei Funktionen auf bequeme Art aneinandergesetzt werden. Wenn der erste Nachbarpunkt nach der Nahtstelle auf einer Geraden mit den beiden letzten Punkten des vorherigen Abschnitts liegt, stoßen auch die beiden benachbarten Bézier-Funktionen tangential aneinander, anderenfalls entsteht eine Ecke mit einem Winkel zwischen den Tangenten, der exakt definierbar ist.
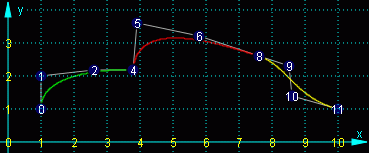
Das nebenstehende Beispiel mit drei einfachen Bézier-Bernstein-Splines 3. Grades (grün, rot und gelb) zeigt beide Varianten: Während der grüne und der rote Spline am Punkt 4 (Punkt 3 liegt darunter) eine Ecke bilden, gehen der rote und der gelbe Spline am Punkt 8 (Punkt 7 liegt darunter) tangential ineinander über, weil die drei Punkte 6, 7 bzw. 8 und 9 auf einer Geraden liegen.
Man darf sich die Silhouette eines Pkw vorstellen: Durch Verändern von Punkt 5 kann der Winkel zwischen Motorhaube und Windschutzscheibe verändert werden, durch Verändern des Punktes 9 kann man vom Fließheck zum Stufenheck übergehen. Diese einfache Möglichkeit, auf die Übergänge Einfluss zu nehmen, wird von dem interaktiv mit einem CAD-System arbeitenden Konstrukteur natürlich geschätzt.

