Man kann sich der Methode der finiten Elemente auf zwei recht unterschiedlichen Wegen nähern, und aus historischer Sicht hat es einige Jahrzehnte gedauert, bis man merkte, dass beide Wege zum gleichen Ziel führen:
- Man ermittelt Lösungen für die Elemente und setzt die Elementlösungen zu Systemlösungen zusammen, indem in jedem Schritt die Anforderungen an die Lösung beachtet werden (Gleichgewicht, Kompatibilität, Elastizitätsgesetz, ...).
- Man betrachtet zunächst das Gesamtsystem und macht einen Ansatz für die zu berechnende Funktion (bei elastostatischen Problemen z. B. für die Verformung), der noch zu bestimmende Freiwerte enthält. Für den Ansatz werden allerdings viele (nur bereichsweise "in einem Element" geltende) Funktionen verwendet, und als Freiwerte nimmt man die Funktionswerte an den Übergangsstellen (Knoten). Dadurch wird die Kompatibilität gewährleistet. Schließlich werden die Freiwerte so bestimmt, dass der Ansatz mit den berechneten Freiwerten die Anforderungen an eine Lösung erfüllt oder besonders gut annähert.
Der Weg 1 (häufig als "strukturdynamischer" Zugang bezeichnet) hat den Vorteil, dass man jederzeit die Konsequenzen der einzelnen Schritte verfolgen kann. Weg 2 ist zweifellos aus mathematischer Sicht eleganter und wird deshalb von Mathematikern und Physikern bevorzugt (auch deshalb, weil er nicht beim physikalischen Modell, sondern erst beim mathematischen Modell ansetzt).
Strukturdynamischer Zugang
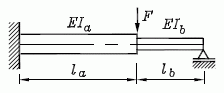
Ingenieure favorisieren im Allgemeinen den oben als Weg 1 bezeichneten Zugang zur FEM, vornehmlich aus dem Grunde, weil man die vielen möglichen Zusatzbedingungen mit stets plausiblen Begründungen realisieren kann, z. B. unterschiedliche Modelle in einem System (Stäbe, Biegeträger, Torsionsstäbe, Scheiben, Platten,Schalen, ...), alle denkbaren Lagervarianten einschließlich Federn und Drehfedern, Gelenke, Scharniere, ...
Am nebenstehend skizzierten einfachen Problem soll dieser Weg plausibel gemacht werden. Der klassische Biegeträger kann mit der Finite-Elemente-Methode exakt nachgebildet werden, so dass eine Einteilung in nur zwei Elemente ausreichend ist. Für diese beiden Elemente (natürlich auch Biegeträger) werden nun nach einem beliebigen Verfahren (z. B. Differenzialgleichung der Biegelinie) die Zusammenhänge zwischen den Schnittkräften an den Knoten und den Verformungen an den Knoten formuliert. Anschließend werden diese Elementlösungen unter Beachtung von Kompatibilität und Gleichgewicht (Schnittkräfte und äußere Lasten an den Knoten) zur Gesamtlösung zusammengesetzt:
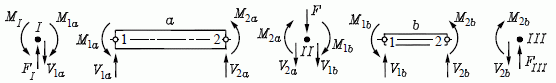
Das Schnittbild mit den beiden Elementen und den 3 Knoten symbolisiert diesen Weg. Genau dieses Beispiel dient im Kapitel "Computer-Verfahren für Biegeprobleme" des Lehrbuchs "Dankert/Dankert: Technische Mechanik" als ausführlich behandeltes Beispiel.
Mathematischer Zugang
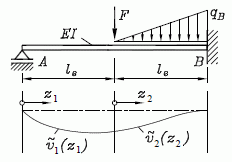
Beim oben als Weg 2 beschriebenen Zugang wird das Gesamtsystem betrachtet. Für die unbekannten Größen (bei Problemen der Technischen Mechanik in der Regel die Verformungen) wird ein Ansatz gemacht, der (wie beim klassischen Verfahren von Ritz) noch Freiwerte enthält. Die Besonderheit besteht darin, dass die Ansatzfunktionen (im Gegensatz zum klassischen Ritz-Verfahren) nur jeweils für einen bestimmten Bereich (ein Element) gelten und dass die Freiwerte die (unbekannten) Verformungsgrößen an den Übergangsstellen (Knoten) sind.
Die nebenstehende Skizze symbolisiert dies: Der für das gesamte System geltende Verschiebungsansatz wird mit bereichsweise geltenden Funktionen formuliert. Zur Bestimmung der Freiwerte in den Ansatzfunktionen sind (abhängig vom aktuellen Problem) verschiedene Wege möglich. Eine besonders elegante Strategie ist möglich, wenn für das Problem ein Minimalprinzip existiert. Für das hier betrachtete Biegeträger-Problem gilt das Minimum vom elastischen Potenzial:
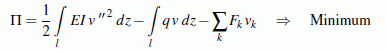
(die Integrationsgrenze l symbolisiert, dass über alle Elemente mit den jeweils dafür geltenden Funktionen zu integrieren ist, der Index k läuft über alle Knoten, an denen äußere Kräfte angreifen).
Genau dieses Beispiel dient im Kapitel "Prinzipien der Mechanik" des Lehrbuchs "Dankert/Dankert: Technische Mechanik" als ausführlich behandeltes Beispiel.
Dieser Weg ist nicht beschränkt auf Probleme, für die ein Extremalprinzip existiert. Er lässt sich ebenso elegant realisieren mit Differenzialgleichungen und den zugehörigen Randbedingungen als Ausgangspunkt. Die theoretische Basis dafür liefert dann die so genannte Methode der gewichteten Residuen. Darauf wird hier nicht eingegangen, weil für die weitaus meisten Probleme der Technischen Mechanik ein Extremalprinzip verfügbar ist.
Empfehlungen
Für eindimensionale Probleme mögen persönliche Präferenzen entscheiden, auf welchem Weg man sich der Finite-Elemente-Methode nähert. Für die komplizierteren (zwei- und dreidimensionalen) Probleme kann als theoretischer Zugang eine Kombination der Wege 1 und 2 empfohlen werden: Man startet mit dem mathematischen Modell (z. B.: Extremalprinzip), wählt geeignete (bereichsweise geltende) Ansatzfunktionen mit geeigneten Freiwerten (z. B.: Knotenverformungen) und kommt über die Extremalbedingungen zu den Gleichungen für die Freiwerte. Dann geht man allerdings noch einen (eigentlich auf diesem Wege nicht erforderlichen) Schritt weiter, und schreibt eine "Elementbeziehungen" auf.
Und weil innere Kräfte bzw. Momente des Systems bei diesem Weg gar nicht auftauchen, sollte man an diesem Punkt (bei Problemen der Technischen Mechanik) an den Weg 1 anknüpfen, weil die in den Elementbeziehungen vorkommenen inneren Kräfte und Momenten bei Problemen der Technischen Mechanik (als Schnittgrößen, Stabkräfte, Spannungen) meistens die wichtigeren Ergebnisse sind.
Diese "gemischte Variante" der Annäherung an die Finite-Elemente-Methode wird auf allen hier publizierten Seiten praktiziert.

