Element-Steifigkeitsbeziehung
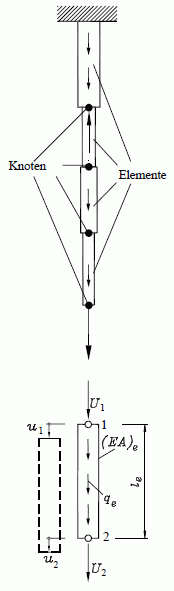
Betrachtet wird eine sehr einfache Struktur (nebenstehende Skizze rechts), die sich aus Stäben mit konstanten Querschnitten zusammensetzt. Die Stäbe sind ausschließlich durch Normalkräfte in Längsrichtung belastet, Einzelkräfte greifen nur an den Verbindungsstellen der Stäbe (Knoten) an. Als verteilte Belastung wird die pro Stab konstante Linienlast q (Eigengewicht) berücksichtigt.
Dieses System wird so zerschnitten, dass die Knoten (einschließlich der äußeren Einzelkräfte) von den Elementen getrennt werden. Man erhält das einfachste finite Element der Elastomechanik, den ausschließlich durch Normalkräfte belasteten geraden Stab.
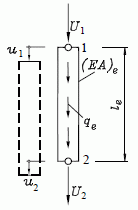
Die am Element angetragenen Kräfte U1 und U2 (Schnittkräfte) und die Linienlast qe werden in gleicher Richtung positiv definiert (man beachte den Unterschied zur Definition der Schnittgrößen in der Technischen Mechanik), die Verschiebungen der Punkte 1 und 2 übereinstimmend mit den Kraftrichtungen. Die elastischen Eigenschaften des Elementes e sind durch die Dehnsteifigkeit (EA)e und die Länge le gegeben.
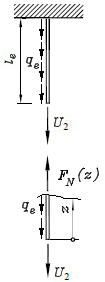
Am Element sind natürlich U1, U2 und die Resultierende der Linienlast qe im statischen
![]()
Die Gesamtverschiebung des Knotens 2 ist die Summe aus der Verschiebung des Knotens 1 und der Verlängerung des Elements infolge der Kraft U2 und der Linienlast qe. Letztere berechnet sich entsprechend nebenstehender Skizze links aus der Integration der Dehnung ε über die Stablänge. Mit der Normalkraft FN = U2 + qe z erfährt der Stab eine Verlängerung
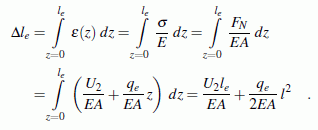
Neben dem Gleichgewicht hat man damit als zweite Beziehung am Element die
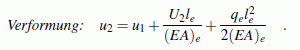
Diese beiden Gleichungen ("Gleichgewicht" und "Verformung") lassen sich umschreiben zu
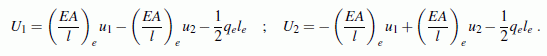
Sie werden zusammengefasst zur
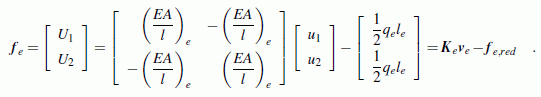
| fe | ⟹ | Element-Kraftvektor, | ||
| ve | ⟹ | Element-Verschiebungsvektor, | ||
| Ke | ⟹ | Element-Steifigkeitsmatrix, | ||
| fe,red | ⟹ | Vektor der reduzierten Elementlasten. |
Mit diesem einfachsten aller Elemente soll nun das einfachste System berechnet werden, das sich daraus bilden lässt, der aus zwei Elementen bestehende Stab.
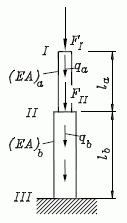
System-Steifigkeitsbeziehung am Beispiel
Der skizzierte Stab ist an den Punkten I und II durch die Kräfte FI bzw. FII und zusätzlich durch das Eigengewicht (repräsentiert durch qa und qb) belastet und bei III gelagert.
Gegeben: Ea ; Aa ; la ; qa ; Eb ; Ab ; lb ; qb ; FI ; FII .
Berechnet werden sollen die Verschiebungen der Punkte I und II und die Lagerkraft bei III.
Natürlich ist diese Aufgabe mit elementaren Mitteln der Festigkeitslehre lösbar, und man kann die Ergebnisse nahezu ohne Rechnung angeben (FIII muss die Summe aus FI, FII und dem Gesamtgewicht sein, die Verschiebung uII entspricht der Längenänderung des Elements b und uI der Summe der Längenänderungen beider Elemente).

Hier soll jedoch der typische Finite-Elemente-Algorithmus demonstriert werden: Die Punkte I, II und III werden als Knoten betrachtet, die die äußere Belastung tragen. Auch die Lagerkraft FIII wird zu den äußeren Kräften gezählt, wie überhaupt alle Knoten zunächst gleichartig behandelt werden. Die Elemente werden durch Schnitte von den Knoten getrennt. Die Schnitte werden unendlich dicht neben den Knoten angebracht, so dass diese keine Längenausdehnung haben, die äußeren Kräfte werden jedoch den Knoten zugeordnet.
Die als Schnittkräfte sichtbar werdenden inneren Kräfte sind nach dem Schnittprinzip der Statik am Element und am Knoten gleich groß mit entgegengesetztem Richtungssinn anzutragen.
Sie werden an beiden Enden beider Elemente (im Folgenden als Elementknoten bezeichnet und in nebenstehender Schnittskizze als kleine Kreise zu sehen) entsprechend der bei der Definition der Elementkräfte erläuterten Regel gleichsinnig angetragen. Diese Richtung gilt allgemein als positive Kraft- und Verschiebungsrichtung. Auch die an den Systemknoten (dicke schwarze Punkte) angreifenden äußeren Kräfte und die Knotenverschiebungen werden dann positiv gezählt, wenn sie in diese Richtung weisen.
Es ergeben sich also drei Knoten, für die jeweils das Knotengleichgewicht erfüllt sein muss, und zwei Elemente, für die die Element-Steifigkeitsbeziehungen gelten müssen:
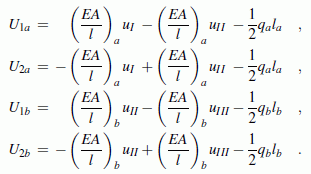
In diesen Element-Steifigkeitsbeziehungen wurden die Kompatibilitätsbedingungen bereits berücksichtigt, indem die Verschiebungen uI, uII und uIII verwendet wurden, so dass die Gleichheit der Verschiebung des Elementknotens 2 des Elements a mit der Verschiebung des Elementknotens 1 des Elements b garantiert ist. Dagegen ist die geometrische Randbedingung (uIII = 0) noch nicht berücksichtigt.
An den Systemknoten müssen die Element-Knotenkräfte (angetragen mit entgegengesetztem Richtungssinn zur Definition am Element) mit den äußeren Kräften im Gleichgewicht sein:
![]()
Aus diesen Kraft-Gleichgewichtsbedingungen an den drei Knoten erhält man durch Einsetzen der oben angegebenen Element-Steifigkeitsbeziehungen (Element-Knotenkräfte U werden durch die Verschiebungen u ausgedrückt) die so genannten System-Steifigkeitsbeziehungen:
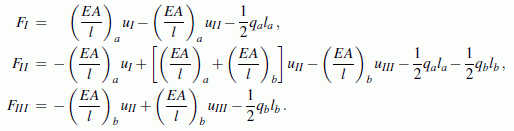
Alle Belastungen (Kräfte FI, FII und FIII und die reduzierten Elementlasten) werden zum System-Kraftvektor f, die drei Knotenverschiebungen uI, uII und uIII werden zum System-Verschiebungsvektor v zusammengefasst, der Zusammenhang zwischen diesen beiden Vektoren wird dann durch die System-Steifigkeitsmatrix K beschrieben:
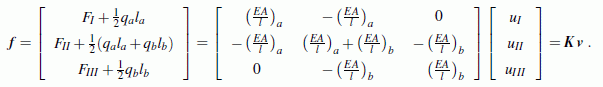
Dieses lineare Gleichungssystem mit 3 Gleichungen enthält genau 3 Unbekannte (uI, uII und FIII), die nun berechnet werden können. Aber:
Der Weg bis zu diesem Gleichungssystem erscheint sicher sehr aufwendig und mühsam. Dafür ist noch eine Rechtfertigung erforderlich:
- Es muss noch gezeigt werden, wo der Vorteil dieses Weges über Element-Steifigkeitsbeziehungen bis zur System-Steifigkeitsbeziehung liegt. Man wird ihn in dem hohen Formalisierungsgrad der einzelnen Schritte finden.
- Das entstandene lineare Gleichungssystem (System-Steifigkeitsbeziehung) hat noch nicht die klassische Form des linearen Gleichungssystems mit allen Unbekannten in einem Vektor. Wie man diese Form sinnvoll erzeugt und welche angenehmen Eigenschaften das dann entstehende Gleichungssystem aus numerischer Sicht hat, wird auf der Seite "Lösung der System-Steifigkeitsbeziehung" beschrieben.

