Methode der finiten Elemente

Richard Courant, "Vater der FEM" (© MFO)

Finite-Elemente-Methode

Die Finite-Elemente-Methode (FEM) basiert auf der Idee, das zu berechnende Gebilde in eine (große) Anzahl einfacher (und damit der Berechnung zugängiger) Elemente zu zerlegen und aus den Elementlösungen unter Berücksichtigung von Kontinuitäts- und Gleichgewichtsbedingungen eine Lösung für das Gesamtsystem zu konstruieren. Diese Bedingungen werden dabei nur an einer endlichen Zahl von Punkten (so genannten Knoten) formuliert.

Der Vorschlag, physikalische Probleme auf diese Weise zu lösen, wurde erstmals 1943 von dem Mathematiker RICHARD COURANT (1888-1972) gemacht, die Zulässigkeit dieses Vorgehens wurde mathematisch einwandfrei bewiesen und die Anwendbarkeit in einer Veröffentlichung an einem Beispiel demonstriert. Der Gedanke wurde jedoch nicht weiter verfolgt, weil vermutlich die Lösung des sich ergebenden (recht umfangreichen) Gleichungssystems abschreckte.

Auf ganz anderem Wege wurden von verschiedenen Ingenieuren (vorwiegend aus dem Flugzeugbau) in der zweiten Hälfte der fünfziger Jahre des 20. Jahrhunderts "Elementlösungen" zu "Gesamtlösungen" zusammengesetzt. Diese eher intuitiv entstandene Methode fand sehr schnell viele Anwender: Die Methode der finiten Elemente wurde erfolgreich eingesetzt, ohne dass der mathematische Nachweis für die Richtigkeit des Verfahrens erbracht war.

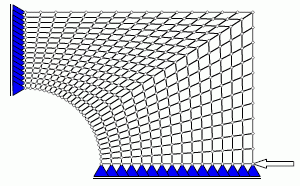
Bauteil wird in Elemente unterteilt

Erst Ende der sechziger Jahre gelangen die mathematische Absicherung der Finite-Elemente-Methode und der Nachweis, dass sie mit dem von Courant vorgeschlagenen Verfahren identisch ist. Anfang der siebziger Jahre erschienen die ersten großen Programmsysteme, deren Einsatzmöglichkeiten weit über die Aufgabenstellungen der Technischen Mechanik hinausgingen.

Heute ist die Methode der finiten Elemente sicher das am meisten benutzte Verfahren, um naturwissenschaftliche und technische Probleme numerisch mit Hilfe des Computers zu lösen. Sie wird für Festigkeitsuntersuchungen, dynamische Probleme und in der Strömungsmechanik ebenso eingesetzt wie in der Thermodynamik, für die Berechnung von Magnetfeldern, in der Gezeitentheorie und für die Wettervorhersage.

Man kann sich der Methode der finiten Elemente auf recht unterschiedlichen Wegen nähern (ähnlich den beiden Wegen, die historisch zu diesem Verfahren führten). Dies wird auf der Seite "Theoretische Zugänge" erläutert.