 Am Beispiel eines Biegeträgers sollen der Aufbau der Elementsteifigkeitsbeziehungen, der Zusammenbau zur Systemsteifigkeitsbeziehung, der Einbau der geometrischen Randbedingungen und die Berechnung der Verschiebungen demonstriert werden.
Am Beispiel eines Biegeträgers sollen der Aufbau der Elementsteifigkeitsbeziehungen, der Zusammenbau zur Systemsteifigkeitsbeziehung, der Einbau der geometrischen Randbedingungen und die Berechnung der Verschiebungen demonstriert werden.
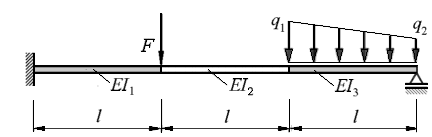
Aufgabe: Für den nebenstehend skizzierten Träger mit stückweise konstanter Biegesteifigkeit soll die Biegeverformung berechnet werden.
Gegeben:
 l = 1 m ; F = 1 kN ; q1 = 2 kN/m ; q2 = 1 kN/m ; EI1 = EI3 = 1 kNm2 ; EI2 = 2 kNm2 .
l = 1 m ; F = 1 kN ; q1 = 2 kN/m ; q2 = 1 kN/m ; EI1 = EI3 = 1 kNm2 ; EI2 = 2 kNm2 .
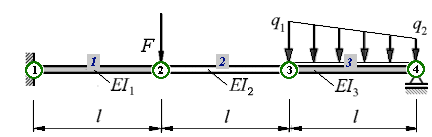
Der Träger wird in 3 finite Elemente unterteilt, dabei entstehen 4 Knoten. Die nebenstehende Skizze zeigt die gewählte Nummerierung.
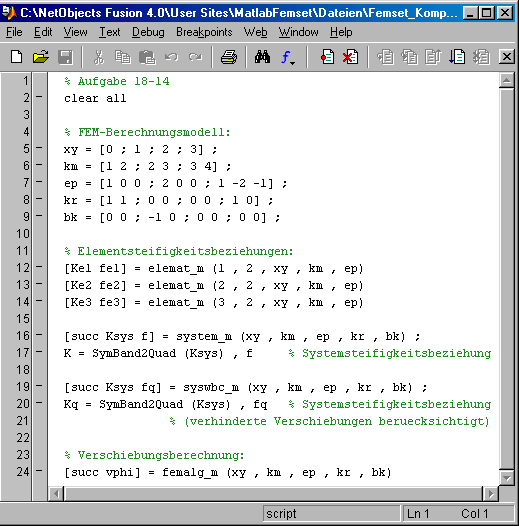 Das Matlab-Interface zum Finite-Elemente-Baukasten Femset gestattet Einblicke in die Zwischenstufen des Algorithmus. Deshalb wird mit dem nebenstehend zu sehenden Matlab-Script zunächst in den Zeilen 5 bis 9 das Berechnungsmodell definiert, danach werden die drei Elementsteifigkeitsbeziehungenen (Zeilen 12 bis 14), die Systemsteifigkeitsbeziehung ohne (Zeile 16) bzw. mit Berücksichtigung der Randbedingungen (Zeile 19) berechnet und in das Command Window ausgegeben. Abschließend werden die Verschiebungen berechnet (Zeile 24).
Das Matlab-Interface zum Finite-Elemente-Baukasten Femset gestattet Einblicke in die Zwischenstufen des Algorithmus. Deshalb wird mit dem nebenstehend zu sehenden Matlab-Script zunächst in den Zeilen 5 bis 9 das Berechnungsmodell definiert, danach werden die drei Elementsteifigkeitsbeziehungenen (Zeilen 12 bis 14), die Systemsteifigkeitsbeziehung ohne (Zeile 16) bzw. mit Berücksichtigung der Randbedingungen (Zeile 19) berechnet und in das Command Window ausgegeben. Abschließend werden die Verschiebungen berechnet (Zeile 24).
Das Berechnungsmodell: In xy stehen die Koordinaten der 4 Knoten, bezogen auf ein (beliebiges) hier im Knoten 1 liegendes Koordinatensystem, km ("Koinzidenzmatrix") enthält die Zuordnung der Knoten zu den Elementen (zu Element 1 gehören Knoten 1 und 2 usw.). In der Elementparametermatrix ep stehen in jeder Zeile 3 Werte für ein Element: Biegesteifigkeit EI, Linienlastintensität am ersten Knoten und Linienlastintensität am zweiten Knoten. Die Matrix der Randbedingungen kr signalisiert für die jeweils zwei Freiheitsgrade der Knoten (Vertikalverschiebung, Biegewinkel) mit einer 1 eine "verhinderte Verschiebung", mit einer 0 die freie Verschiebungsmöglichkeit. In der Matrix der diskreten Lasten bk können analog dazu für jeden Knoten eine äußere Einzellast und ein äußeres Moment definiert werden.
Die Zahlenwerte der Aufgabenstellung wurden bewusst so gewählt, dass man in den Elementsteifigkeitsmatrizen die Werte aus der hier angegebenen Formel wiedererkennt (es wurden auch im Berechnungsmodell konsequent die Einheiten kN und m für alle Werte verwendet, so dass sich die Verschiebungen auch mit der Dimension m ergeben).
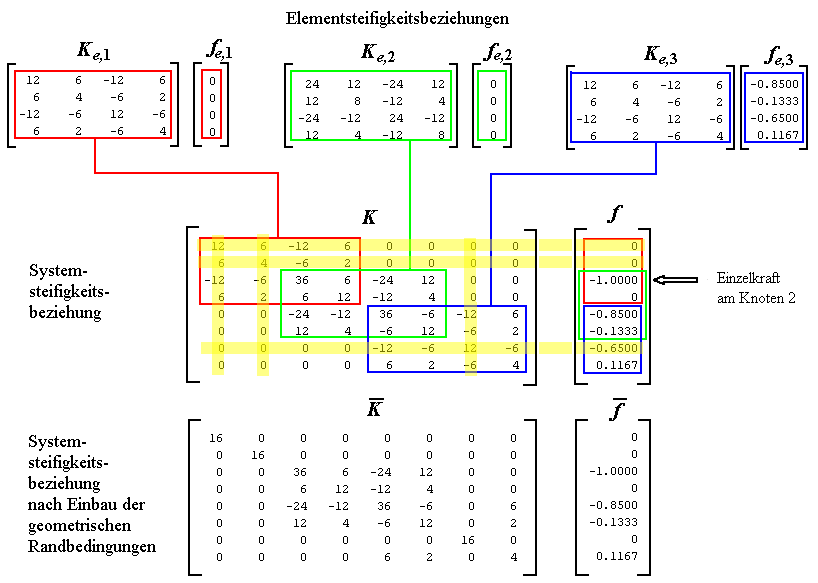
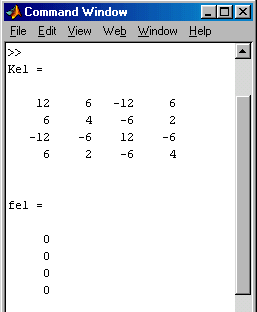 Nebenstehend sieht man nur den ersten Teil (Ausgabe des Ergebnisses der Berechnung in Zeile 12) des Command Windows (Elementsteifigkeitsbeziehung des Elements 1). Alle übrigen Ausgaben sind im nachfolgenden Bild so zusammengestellt worden, dass man die Zusammenhänge zwischen Elementsteifigkeitsbeziehungen und Systemsteifigkeitsbeziehung erkennen kann.
Nebenstehend sieht man nur den ersten Teil (Ausgabe des Ergebnisses der Berechnung in Zeile 12) des Command Windows (Elementsteifigkeitsbeziehung des Elements 1). Alle übrigen Ausgaben sind im nachfolgenden Bild so zusammengestellt worden, dass man die Zusammenhänge zwischen Elementsteifigkeitsbeziehungen und Systemsteifigkeitsbeziehung erkennen kann.
Man sieht, dass die Elementsteifigkeitsbeziehungen direkt auf die entsprechenden Positionen in die Systemsteifigkeitsbeziehung eingespeichert werden. Auf den Positionen, auf die Anteile aus verschiedenen Elementsteifigkeitsbeziehungen gelangen (hier sind es die Bereiche, wo sich die Anteile des Elements 2 mit einem der beiden anderen Elemente überlappen), werden diese addiert. Anschließend wurde im Systembelastungsvektor die äußere Einzellast am Knoten 2 ergänzt.
In der Systemsteifigkeitsbeziehung (K und f) sind zunächst die geometrischen Randbedingungen (verhinderte Verschiebungen) unberücksichtigt. Am Knoten 1 sind beide Verschiebungen (Vertikalverschiebung, Biegewinkel), am Knoten 4 nur die Vertikalverschiebung verhindert. Das bedeutet, dass im Gleichungssystem
![]()
im Vektor v auf den Positionen 1, 2 und 7 jeweils eine 0 steht, und im Vektor f müssen auf den entsprechenden Positionen unbekannte Kräfte (Lagerreaktionen) eingesetzt werden. Bei der Multiplikation Kv sind also (infolge der Nullelemente in v) die Spalten 1, 2 und 7 der Matrix Kbedeutungslos. Diese Spalten und die Nullelemente in v könnten also gestrichen werden. Wenn gleichzeitig auch die Zeilen 1, 2 und 7 (in K und f) gestrichen werden, verschwinden diese 3 Gleichungen (und auch die drei Unbekannten in f) aus dem Gleichungssystem.
In der Systemsteifigkeitsbeziehung sind diese Zeilen und Spalten gelb unterlegt. Wenn sie gestrichen werden (Berücksichtigung verhinderter Verschiebungen durch "Zeilen-Spalten-Streichen"), verbleibt ein Gleichsungssystem mit nur noch 5 Gleichungen (und 5 unbekannten Verschiebungen), wobei die Symmetrie der Matrix K erhalten bleibt.
In Femset wird eine alternative Strategie zur Berücksichtigung der Randbedingungen realisiert: Die Zeilen und Spalten werden nicht gestrichen, sondern durch die drei Gleichungen v1 = 0, φ1 = 0 und v4 = 0 ersetzt. Die auf diese Weise modifizierte Systemsteifigkeitsbeziehung ist im nachfolgenden Bild unten zu sehen. Dem geringfügigen Nachteil dieser Strategie, dass sich die Anzahl der Gleichungen nicht reduziert, stehen als Vorteile die Einsparung eines aufwendigen Umspeicherungsprozesses und ein Ergebnisvektor v nach der Lösung des Gleichungssystems gegenüber, der alle Verschiebungen des Systems (auch die Nullverschiebungen) enthält.
 Es fällt auf, dass die Gleichungen, die die verhinderten Verschiebungen realisieren, statt der zu erwartenden 1 eine 16 auf der Hauptdiagonalen haben. Natürlich ist 16 v1 = 0 gleichwertig mit v1 = 0. Weil die Elemente der Steifigkeitsmatrizen außerordentlich groß werden können und bei stark unterschiedlichen Größenordnungen der Elemente der Koeffizientenmatrix die Gefahr numerischer Instabilität besteht, setzt Femset einen Wert in der Größenordnung der übrigen Matrixelemente auf diese Positionen.
Es fällt auf, dass die Gleichungen, die die verhinderten Verschiebungen realisieren, statt der zu erwartenden 1 eine 16 auf der Hauptdiagonalen haben. Natürlich ist 16 v1 = 0 gleichwertig mit v1 = 0. Weil die Elemente der Steifigkeitsmatrizen außerordentlich groß werden können und bei stark unterschiedlichen Größenordnungen der Elemente der Koeffizientenmatrix die Gefahr numerischer Instabilität besteht, setzt Femset einen Wert in der Größenordnung der übrigen Matrixelemente auf diese Positionen.
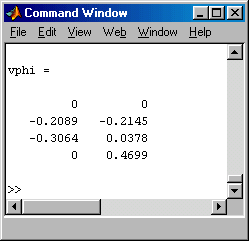
Schließlich liefert das Matlab-Script (Zeile 24) noch die sich aus der Lösung des Gleichungsystems ergebenden Knotenverschiebungen ab (siehe nebenstehenden Ausschnitt aus dem Command Window, in der linken Spalte stehen die Vertikalverschiebungen, in der rechten Spalte die Biegewinkel an den vier Knoten).
Das hier beschriebene Matlab-Script ist als Lösung der Aufgabe 18-14 verfügbar und steht dort gemeinsam mit allen verwendeten DLLs und Matlab-Functions zum Download bereit.
Unter TM-interaktiv existiert ein Programm "Gerader Biegeträger", das die hier betrachteten Biegeträger als Sonderfall enthält (es arbeitet auf der Basis der hier verwendeten Ansatzfunktion). Damit kann das behandelte Beispiel nachgerechnet werden.

