Rotationssymmetrische Kreis- und Kreisringplatten

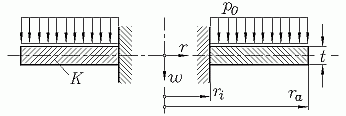
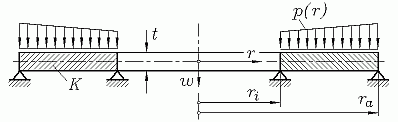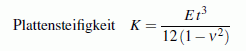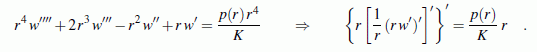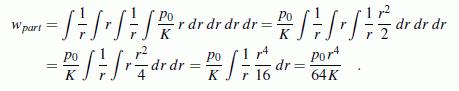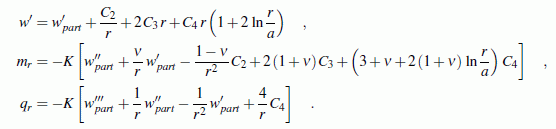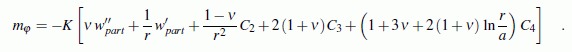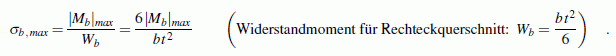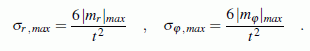Verformungs-Differentialgleichung, Schnittgrößen

Betrachtet werden dünnwandige (Dicke t) elastische Kreis- oder Kreisringplatten, die rotationssymmetrisch belastet und gelagert sind. Eine Koordinate r genügt zur Beschreibung eines Punktes (eigentlich eines Kreises) der Mittelfläche der Platte. Als Belastungen sind Flächenlasten p(r) (Dimension z. B.: N/mm²), gegebenenfalls auch konstante Linienlasten auf einem Kreis und bei der vollen Kreisplatte (Innenradius r_i = 0) auch eine Einzelkraft im Zentrum zugelassen.

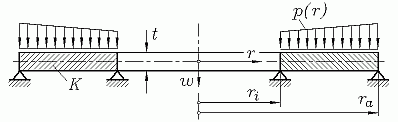
Die elastischen Eigenschaften der Platte (Elastizitätsmodul E und Querkontraktionszahl ν) werden gemeinsam mit der Plattendicke t in der so genannten

zusammengefasst. Für die Verformung der Platten-Mittelfläche, die durch w(r) beschrieben wird, gilt die Differenzialgleichung (der Strich kennzeichnet Ableitungen nach r):

Die Integration dieser Eulerschen Differenzialgleichung 4. Ordnung erzeugt vier Integrationskonstanten, für deren Bestimmung in der Regel (bei der Kreisringplatte) zwei Randbedingungen am Innen- und zwei Randbedingungen am Außenrand formuliert werden können. Dies können (wie bei der Verformungsberechnung des Biegeträgers) Aussagen über die Absenkung w und deren 1. Ableitung nach r und Aussagen über das Biegemoment m_rund die Querkraft q_r sein. Für diese beiden Schnittgrößen gelten die Formeln:

Weil die Schnittfläche zwar eine feste Höhe (Plattendicke h), aber keine feste Breite (wie beim Biegeträger) hat, sind die Schnittgrößen auf die Länge bezogen: Das Biegemoment kann z. B. in der Dimension Nmm/mm = N angegeben werden, die Querkraft in der Dimension N/mm.

Lösung der homogenen Differenzialgleichung

Für die homogene Differenzialgleichung

wird auf der Seite "Eulersche Differenzialgleichungen" als zuverlässig funktionierende Strategie, n linear unabhängige Partikulärlösungen (und damit die allgemeine Lösung der homogenen Differenzialgleichung) zu finden, die Substitution r = e ^t empfohlen. Dort findet man auch die Formeln, nach denen sich die Ableitungen transformieren und auch die transformierte homogene Eulersche Differenzialgleichung 4 . Ordnung in allgemeiner Form. Das Ergebnis der Transformation ist eine lineare Differenzialgleichung mit konstanten Koeffizienten. Für das hier betrachtete Problem ergibt sich (die Punkte deuten Ableitungen nach t an): Nun kann die Strategie angewendet werden, die auf der Seite "Lineare Differenzialgleichungen mit konstanten Koeffizienten" beschrieben wird: Mit dem Ansatz w_hom = e ^λ t kommt man über die charakteristische Gleichung zu den λ-Werten, mit denen das Fundamentalsystem aufgeschrieben werden kann: Nach der hier formulierten Regel, wie man bei Doppellösungen Defizite im Fundamentalsystem vermeidet, kann die allgemeine Lösung der homogenen linearen Differenzialgleichung mit konstanten Koeffizienten aufgeschrieben werden: Die Rücksubstitution (e ^t  = r  →  t = ln r) liefert die Lösung der homogenen Eulerschen Differenzialgleichung In dieser Form hat die Lösung (zumindest aus der Sicht des Ingenieurs) noch einen (mehr als kleinen) "Schönheitsfehler": Das Argument des natürlichen Logarithmus ist dimensionsbehaftet (Länge). Mit einem kleinen Trick kann dieser Mangel geheilt werden. Weil die Integrationskonstanten hier noch völlig beliebige Werte annehmen können, dürfen z. B. diese beiden Integrationskonstanten so modifiziert werden: mit der beliebigen (konstanten) Länge a. Damit kann die Lösung der homogenen Eulerschen Differenzialgleichung umgeschrieben werden. Über kommt man zu einer Form mit dimensionslosem Argument für den natürlichen Logarithmus:

Partikulärlösung für die inhomogene Differenzialgleichung

Für die Suche nach einer Partikulärlösung der Differenzialgleichung der rotationssysmmetrischen Platte gibt es eine besonders elegante und sichere Strategie, weil sich dies Differenzialgleichung wie folgt umschreiben lässt:

Man überzeugt sich leicht durch Ausdifferenzieren des kompakten Ausdrucks der rechts stehenden Variante, dass diese gleichwertig ist mit der links angegebenen Differenzialgleichung. Damit ist die Möglichkeit gegeben, durch viermaliges Integrieren entsprechend die allgemeine Lösung direkt zu berechnen, wenn bei jedem Integrationsschritt die jeweilige Integrationskonstante hinzugefügt und in den weiteren Schritten auch mit integriert wird. Das Ergebnis ist dann der oben bereits angegebene Anteil der homogenen Differenzialgleichung und die zusätzlich erforderliche Partikulärlösung der inhomogenen Differenzialgleichung.

Weil die Lösung der homogenen Differenzialgleichung aber völlig unabhängig vom konkreten Problem ist, braucht sie nicht jedes Mal neu berechnet zu werden, und man kann sich darauf beschränken, durch die vierfache Integration (ohne Berücksichtigung der Integrationskonstanten) nur die Partikulärlösung zu berechnen.

Beispiel: Es soll eine Partikulärlösung für die inhomogene Differenzialgleichung bei einer konstanten Flächenlast p(r) = p₀ gefunden werden. Nach der oben angegebenen Integralformel berechnet man (ohne Berücksichtigung der in jedem Schritt entstehenden Integrationskonstanten):

Randbedingungen, Schnittgrößen, Spannungen

Für das Aufschreiben der Randbedingungen werden neben der Verschiebung w und deren Ableitung w' auch die Beziehungen für das Biegemoment m_r und die Querkraft q_r benötigt. Aus der allgemeinen Lösung

berechnet man unter Verwendung der oben angegebenen Formeln: Damit können die Randbedingungen formuliert werden, aus denen die Integrationskonstanten berechnet werden, so dass schließlich der Verschiebungsverlauf w(r) und die Schnittgrößenverläufe m_r(r) und q_r(r) bekannt sind. Während für die Kreisringplatte zwei Randbedingungen am Innenrand und zwei Randbedingungen am Außenrand formuliert werden können (eventuell auch noch vier Übergangsbedingungen an Übergangsstellen), müssen für die Kreisplatte (der Innenrand fehlt) zwei Integrationskonstanten aus folgender Überlegung festgelegt werden: Weil sowohl die Durchbiegung als auch die Schnittgrößen auch für r = 0 endlich sein müssen, kann für die beiden Integrationskonstanten C₂ und C₄ nur C₂ = C₄ = 0 gelten.

Es gibt noch eine (für die Randbedingungsformulierung nicht benötigte) Schnittgröße m_φ(r), die in radialen Schnitten auftritt. Sie wird dadurch hervorgerufen, dass sich die Querkontraktion infolge der Biegung nicht frei ausbilden kann. Das Biegemoment m_r erzeugt (wie das Biegemoment M_b bei der Theorie des Biegeträgers) am oberen und unteren Rand Spannungen und damit Dehnungen mit unterschiedlichen Vorzeichen. Beim Biegeträger können diese Dehnungen sich frei ausbilden (ein Rechteckquerschnit z. B. wird zum Trapez), bei der Platte ist dies nicht möglich, weil die Nachbarstreifen genau diese Ausdehnung auch versuchen. Das durch die Verhinderung der Querdehnung entstehende Moment

kann bei bekannten Integrationskonstanten folgendermaßen berechnet werden: Während die Schubspannungen, die durch die Querkräfte q_r erzeugt werden, (wie beim Biegeträger) in der Regel vernachlässigt werden können, treten (auch wie beim Biegeträger) die größten Biegespannungen am oberen bzw. unteren Rand auf. Die Analogie zum Biegeträger liefert dafür die Formel: Die Maximalspannung in einem Schnitt errechnet man (vgl. Kapitel "Biegung") für den Biegeträger mit Rechteckquerschnitt (Breite b, Höhe t) nach In dieser Formel darf man sich M_b/b als das auf die Schnittbreite b bezogene Biegemoment des Biegeträgers vorstellen. Die Biegemomente m_r bzw. m_φ der Platte sind aber schon auf die Schnittbreite bezogen, so dass man in der Spannungsformel des Biegeträgers nur M_b/b durch das entsprechende Biegemoment der Platte ersetzen muss. Man erhält die
Formeln für die maximalen Biegespannungen in der Kreis- bzw. Kreisringplatte:

Beispiel

Ein komplett durchgerechnetes Beispiel (die nebenstehend skizzierte Kreisringplatte, am Innenrand starr eingespannt, am Außenrand frei) findet man auf der Seite "Rotationssysmmetrische Kreisringplatte, Beispiel".