Krümmungsradius und Krümmungskreis

Krümmungskreise ebener Kurven

Krümmungskreise an eine Bahnkurve

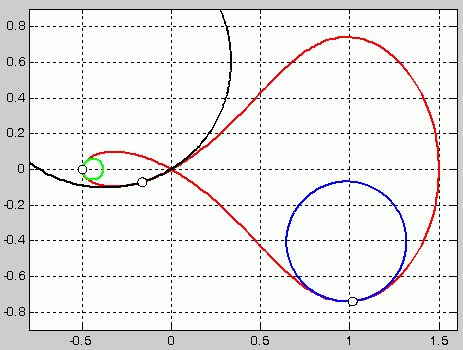
Der Krümmungskreis schmiegt sich an eine Kurve in der Umgebung eines Berührungspunktes optimal an. Die nebenstehende Abbildung zeigt für drei Punkte der (rot gezeichneten) Kurve die (blau, schwarz bzw. grün gezeichneten) Krümmungskreise (die Kurve ist die Bahnkurve eines Punktes einer schwingenden Kurbelschleife, siehe die Animation weiter unten). In der Regel gibt es für jeden Punkt einer Kurve einen anderen Krümmungskreis mit einem eigenen Krümmungsmittelpunkt und einem eigenen Krümmungsradius.

Wozu braucht man das?

In der Technischen Mechanik spielt der Krümmungsradius in verschiedenen Bereichen eine wichtige Rolle, zum Beispiel:

• Bei einem Biegeträger ist das Biegemoment umgekehrt propotional zum Krümmungsradius des verformten Trägers. Auf dieser Basis wird im Kapitel "Verformungen durch Biegemomente" die nichtlineare Differenzialgleichung der Biegelinie hergeleitet.
• Die Normalbeschleunigung bei einer Bewegung auf einer gekrümmten Bahn wird nach der Formel a_n=v²/ρ berechnet (mit der Bahngeschwindigkeit v und dem Krümmungsradius der Bahnkurve ρ). Dies ist in der Regel die wichtigste (weil deutlich größte) Komponente der Gesamtbeschleunigung.

Definitionen

Die oben verwendete Formulierung des "optimalen Anschmiegens" lässt sich auf unterschiedliche Weise in mathematisch verwertbare Definitionen fassen. Die erste Definition lehnt sich an die Definition der Tangente an eine Kurve an: Zwei Punkte definieren eindeutig eine Gerade, die man als Sekante bezeichnet, wenn die beiden Punkte auf einer Kurve liegen. Nähern sich diese beiden Punkte nun immer weiter an, bis sie schließlich im Grenzübergang zusammenfallen, dann wird die Sekante zur Tangente an die Kurve in diesem Punkt. Analog dazu wird definiert:

Völlig gleichwertig mit dieser ist die folgende Definition:

Nachfolgend wird die Definition 2 benutzt, um die benötigten Formeln herzuleiten.

Formeln für den Krümmungsradius

Gegeben sei eine Funktion in Parameterdarstellung

Dies ist keine Einschränkung der Allgemeinheit, weil jede Funktion y=f(x) auch als x=t ,  y=f(t) dargestellt werden kann. Gesucht wird ein Kreis (auch dafür wird die Parameterdarstellung verwendet)

der mit dieser Funktion in einem durch die Koordinaten x und y gegebenen Punkt auch in den beiden Ableitungen y' und y'' übereinstimmt. Für den Kreis werden diese Ableitungen gebildet:

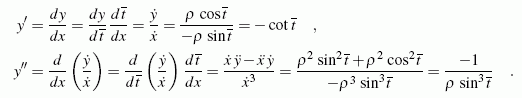
Aus

kann t eliminert werden, und man erhält eine Formel für ρ:

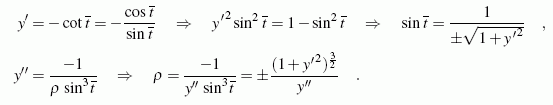
Auf entsprechendem Wege erhält man aus

eine Formel für die Parameterdarstellung der Funktion. Weil ein Radius natürlich einen positiven Wert haben muss, wird für die zweite Ableitung, die positiv oder negativ sein kann, der Absolutwert genommen, und es ergeben sich folgende ...

Formeln für den Krümmungsradius:

Die Funktion, für die ein Krümmungsradius gesucht ist, kann als y = f(x) gegeben sein (dann ist die linke Formel zuständig) oder in Parameterdarstellung als x(t) , y(t) (dann benutzt man die rechte Formel). Nach Bilden der Ableitungen müssen die Koordinaten des Punktes eingesetzt werden, für den der Krümmungsradius berechnet werden soll. Der reziproke Wert des Krümmungsradius wird als Krümmung der Kurve in dem entsprechenden Punkt bezeichnet.

Koordinaten des Krümmungsmittelpunktes

Die oben in allgemeiner Form aufgeschriebene Funktion des Krümmungskreises wird nach den Koordinaten des Mittelpunktes umgestellt:

Um das Vorzeichenproblem mit der Wurzel zu vermeiden, wird auf die oben erreichten Zwischenergebnisse

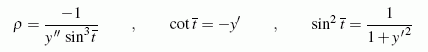
zurückgegriffen, mit denen man zum Beispiel folgende Formeln erhält:

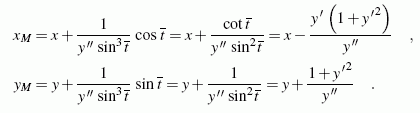
Für die in Parameterdarstellung gegebene Funktion errechnet man auf entsprechendem Wege analoge Formeln, schließlich ergeben sich die

Koordinaten des Krümmungsmittelpunktes:

Auch hier müssen nach dem Bilden der Ableitungen auf der rechten Seite die Koordinaten des Punktes eingesetzt werden, für den die Mittelpunktkoordinaten des Krümmungskreises berechnet berechnet werden sollen.

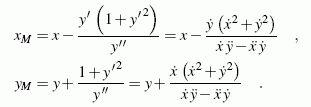
Evolute und Evolvente

Der geometrische Ort aller Krümmungsmittelpunkte einer Kurve heißt Evolute, die Kurve selbst ist die Evolvente dieser Evolute. Diese Kurven spielen in der Verzahnungsgeometrie eine wichtige Rolle.

Beispiel 1

Man berechne für die Funktion y = ax² allgemein den Krümmungsradius ρ(x) und die Koordinaten der Krümmungsmittelpunkte x_M(x) und y_M(x). Für a = 0,5 sind die Krümmungsradien, die zu den Punkten (0;0) bzw. (1;0,5) gehören, und die Parameterdarstellung der Evolute anzugeben.

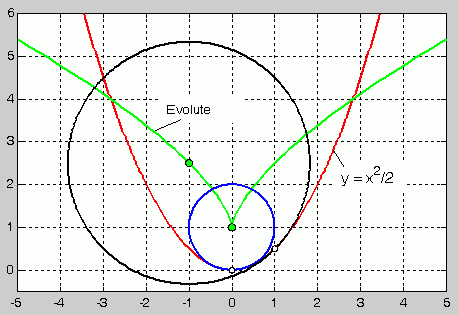
Funktion (rot gezeichnet) mit zwei Krümmungskreisen und Evolute

Die Funktion und ihre ersten beiden Ableitungen

werden in die oben angegebenen Formeln eingesetzt:

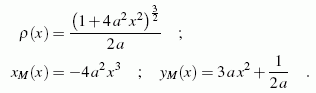
Die berechneten Formeln für die Koordinaten der Krümmungsmittelpunkte x_M(x) und y_M(x) können als Parameterdarstellung (Parameter ist x) der Evolute angesehen werden. Für a = 0,5 erhält man also mit

die Parameterdarstellung der Evolute. In der oben zu sehenden Graphik sind die Funktion y = x²/2 rot, die beiden speziellen Krümmungskreise blau bzw. schwarz und die Evolute grün gezeichnet.

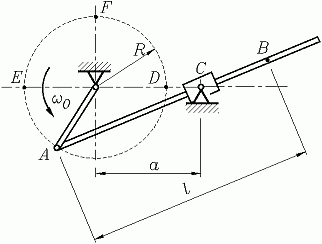
Beispiel 2

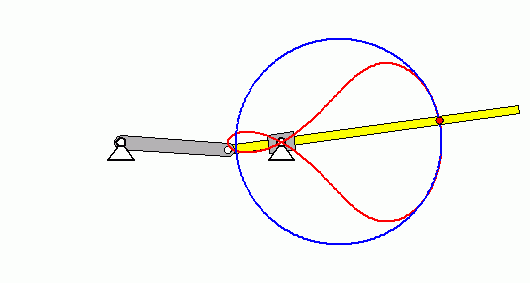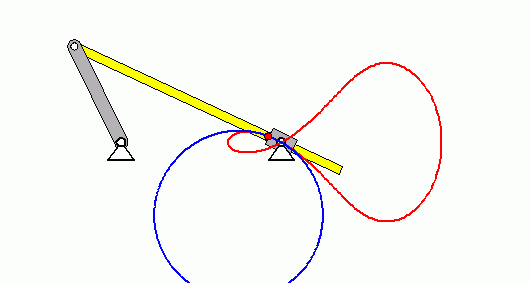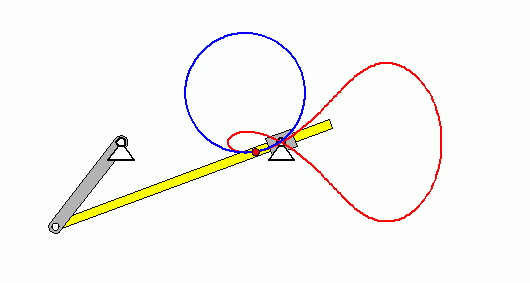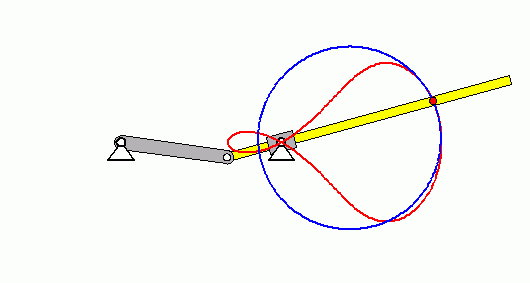
Der nebenstehend skizzierte Mechanismus ist eine so genannte "Schwingende Kurbelschleife". Die Kurbel dreht sich mit der konstanten Winkelgeschwindigkeit ω₀.

Gegeben: R ;  ω₀ ;  a/R = 1,5 ;  l/R = 2 .

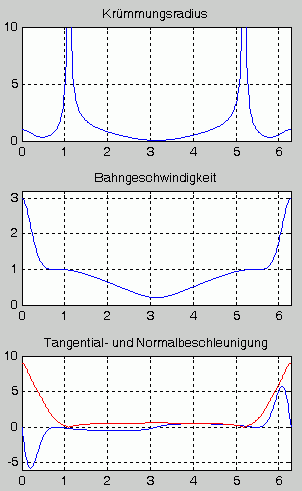
1. Für einen kompletten Kurbelumlauf sind der Krümmungsradius ρ(φ), die Bahngeschwindigkeit des Punktes B v(φ), seine Tangentialbeschleunigung a_t(φ) und Normalbeschleunigung a_n(φ) graphisch darzustellen (φ = ω₀t).
2. Es soll die Bahnkurve des Punktes B dargestellt und daran verdeutlicht werden, dass sich der Krümmungsradius bei einer solchen Kurve ständig ändert.

Die Bestimmung der Bahnkurve ist als Fragestellung einer Aufgabe aus dem Kapitel "Kinematik des Punktes" gefordert. Das Ergebnis findet man im Internet im Bereich "Lösungen der Übungsaufgaben". Die Kurve kann sinnvoll nur in Parameterdarstellung angegeben werden. Mit einem kartesischen Koordinatensystem mit dem Ursprung im Punkt C erhält man, wenn sich der Punkt A der Kurbel zum Zeitpunkt t = 0 im Punkt D befindet:

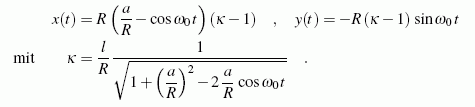
Das Bilden der beiden ersten Ableitungen dieser Funktionen, die man für das Aufschreiben von Krümmungsradius und Krümmungsmittelpunkt benötigt, ist recht mühsam (aber durchaus auch noch "von Hand" beherrschbar). Man ist gut beraten, sich vom Computer unterstützen zu lassen.

Die (tangential gerichtete) Bahngeschwindigket errechnet man aus den Geschwindigkeitskomponenten, und die Tangentialbeschleunigung ist die Ableitung der Bahngeschwindigkeit nach der Zeit:

Für die (senkrecht zur Tangente an die Bahnkurve gerichtete) Normalbeschleunigung

wird zusätzlich der Krümmungsradius benötigt, der nach den oben angegebenen Formeln berechnet wird. Nebenstehend sieht man die graphische Darstellung der Funktionen. Man erkennt, dass die (rot gezeichnete) Normalbeschleunigung größere Werte annimmt als die Tangentialbeschleunigung. Ihr Maximalwert liegt hier nicht im Bereich besonders kleiner Krümmungsradien, weil das Quadrat der Geschwindigkeit im Zähler des Bruchs größeren Einfluss hat. Typisch ist, dass die Tangentialbeschleunigung positive und negative Werte annehmen kann, die Normalbeschleunigung wird dagegen immer positiv angegeben, weil sie stets zum Krümmungsmittelpunkt gerichtet ist.

Nachfolgend sieht man in der Animation die rot dargestellte Bahnkurve des Punktes B und die sich ständig ändernden (blau gezeichneten) Krümmungskreise: