Anfangs-, Rand- und Eigenwertprobleme

Definitionen

Die Allgemeine Lösung einer Differenzialgleichung n-ter Ordnung

enthält noch n unabhängige Parameter (Integrationskonstanten), repräsentiert also eine Kurvenschar. In der Regel interessiert jedoch nur eine spezielle Lösung für ein vorgegebenes Problem, so dass die freien Parameter aus n Zusatzbedingungen bestimmt werden müssen. Abhängig vom Ort, für den diese Bedingungen formuliert werden, unterscheidet man Anfangs- und Randwertprobleme:

• Bei Anfangswertproblemen n-ter Ordnung werden der Funktionswert und die Werte für die ersten n-1 Ableitungen an einer Stelle x₀ vorgegeben:
  
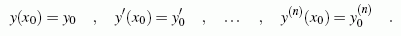
• Bei Randwertproblemen n-ter Ordnung werden an mindestens zwei verschiedenen Stellen insgesamt n Aussagen über die Funktionswerte und/oder Ableitungen bis zur (n-1)-ten Ordnung vorgegeben. Dabei kann eine einzelne Bedingung auch Funktionswert und Ableitungen miteinander verknüpfen.
• Ein wichtiger Spezialfall der Randwertprobleme ist das "Lineare Eigenwertproblem": Eine homogene lineare Differenzialgleichung mit homogenen Randbedingungen hat immer die (nicht interessierende) so genannte "triviale Lösung" y ≡ 0. Das Randwertproblem enthält aber einen (zunächst unbekannten) Parameter λ, der so bestimmt werden kann, dass auch nichttriviale Lösungen möglich sind. Von praktischem Interesse sind in der Regel genau diese "Eigenwerte" λ.

Theoretisch bilden die n Anfangs- oder Randbedingungen ein Gleichungssystem mit n Unbekannten (den Integrationskonstanten), die durch Lösung des Gleichungssystems berechnet werden können (bei den Eigenwertproblemen ist es ein homogenes Gleichungssystem mit der Frage, wann nichttriviale Lösungen möglich sind). Dieser Weg ist bei vielen Problemen nicht durchführbar, weil das Anfangs- bzw. Randwertproblem nicht analytisch lösbar ist. Allerdings müssen auch für eine numerische Lösung die Anfangs- bzw. Randbedingungen formuliert werden.

Beispiele

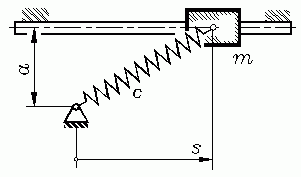
Anfangswertproblem 2. Ordnung: Eine Masse m kann sich auf der horizontalen Führung reibungsfrei bewegen. Sie ist durch eine (lineare) Feder gefesselt, die im entspannten Zustand die Länge b hat. Die Masse wird um s_anf ausgelenkt und zum Zeitpunkt t=0 ohne Anfangsgeschwindigkeit freigelassen.

Die Differenzialgleichung, die die Bewegung beschreibt, findet man am einfachsten mit dem Prinzip von d'Alembert (Kapitel "Kinetik des Massenpunktes"). Es ist ein Anfangswertproblem, weil man die beiden zusätzlichen Bedingungen für die Differenzialgleichung 2. Ordnung an der gleichen Stelle aus der Aufgabenstellung entnehmen kann: Zum Zeitpunkt t=0 ist die Masse bei s=s_anf und hat noch keine Geschwindigkeit v=ds/dt. Damit kann das Anfangswertproblem 2. Ordnung so formuliert werden:

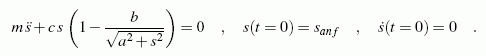
Dieses nichtlineare Anfangswertproblem kann nur numerisch gelöst werden (komplette Lösung hier).

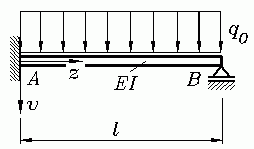
Randwertproblem 4. Ordnung: Ein Biegeträger mit konstanter Biegesteifigkeit EI trägt eine konstante Linienlast q₀. Er ist am linken Rand starr eingespannt (keine Durchbiegung v und horizontale Tangente der Biegelinie v'). Am rechten Rand ist er gelenkig (momentenfrei) gelagert (keine Durchbiegung v und kein Biegemoment). Weil das Biegemoment proportional zur zweiten Ableitung der Biegelinie ist, muss die zweite Ableitung am rechten Rand verschwinden. Zur Berechnung der Biegelinie kann mit der in diesem Fall besonders einfachen Differenzialgleichung der Biegeline 4. Ordnung folgendes Randwertproblem formuliert werden:

Dieses lineare Randwertproblem kann analytisch gelöst werden. Die komplette Lösung findet man im Kapitel "Verformungen durch Biegemomente".

Lineares Eigenwertproblem 4. Ordnung: Ein Biegeträger mit konstanter Biegesteifigkeit EI und konstanter Massebelegung ρA kann Schwingungen senkrecht zur Trägerlängsachse ausführen. Der Träger ist am linken Rand starr eingespannt (keine Durchbiegung v und horizontale Tangente der Biegelinie v'). Am rechten Rand ist er gelenkig (momentenfrei) gelagert (keine Durchbiegung v und kein Biegemoment). Für die Analyse der Biegeschwingungen kann folgendes Eigenwertproblem formuliert werden:

Die Lösung dieser Aufgabe wird in dem Skript "Biegeschwingungen gerader Träger" (PDF, 37 Seiten) neben zahlreichen anderen Aufgaben ausführlich behandelt und nach verschiedenen Verfahren gelöst. Im Internet findet man die Lösung über die Seite "Biegeschwingungen gerader Träger".

Komplizierte Randbedingungen, Übergangsbedingungen

Bei Problemen der Technischen Mechanik sind die Zusatzbedingungen, mit denen die allgemeine Lösung der Differenzialgleichung zur speziellen Lösung für ein vorgegebenes Problem wird, häufig nicht allein durch das Vorschreiben von Funktionswerten bzw. Ableitungen an bestimmten Punkten möglich. Zwei zusätzliche Schwierigkeiten tauchen auf:

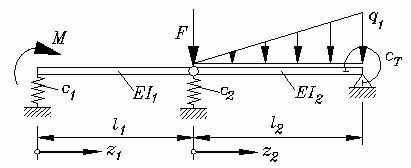
• Als Randbedingung muss eine Beziehung formuliert werden, die den Funktionswert und seine Ableitungen an einer Stelle miteinander verknüpfen. So lautet zum Beispiel für den skizzierten Biegeträger eine Randbdingung am rechten Rand (der Träger wird dort durch eine Drehfeder gestützt):
  
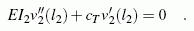
• Dieser Biegeträger zeigt auch das zweite typische Problem: Die Differenzialgleichungen müssen abschnittsweise formuliert werden, weil Unstetigkeiten in der Lösungsfunktion und/oder ihrer Ableitungen zu erwarten sind (bei diesem Beispiel führt das Gelenk zu einem "Knick" in der Biegelinien, die Kraft F und die Feder sorgen für einen Sprung im Querkraftverlauf (3. Ableitung). Zwar sind die Differenzialgleichungen für die beiden Bereiche
  
  besonders einfach lösbar, aber der Weg von der allgemeinen Lösung zur speziellen Lösung dieses Problems verursacht einigen Aufwand. Insgesamt entstehen 8 Integrationskonstanten, für die 8 Rand- und Übergangsbedingungen formuliert werden müssen. Eine der (insgesamt 4) Randbedingungen wurde oben bereits angegeben. Von den 4 Übergangsbedingungen ist die Bedingung, dass die Funktion v(z) (nicht ihre Ableitung!) an der Übergangstelle stetig sein muss, mit
  
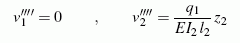  noch vergleichsweise einfach. Die Bedingung, dass dort die inneren Kräfte (Querkräfte links und rechts vom Gelenk) mit der äußeren Kraft F und der Federkraft ein Gleichgewichtssystem bilden müssen, sieht allerdings so aus: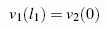
  

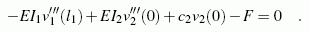
Das skizzierte Problem ist eine Randwertaufgabe 4. Ordnung, bei der die Schwierigkeiten fast ausschließlich durch die Rand- und Übergangsbedingungen entstehen (schließlich ist für die Berechnung der Integrationskonstanten ein lineares Gleichungssystem mit 8 Unbekannten zu lösen). Es ist aber durchaus noch analytisch lösbar, auch wenn die Unterstützung durch einen Computer empfohlen werden muss. Die komplette Rechnung findet man hier.