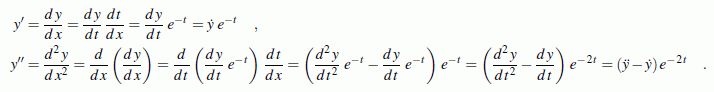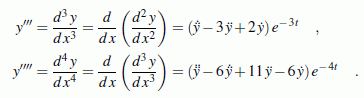Eulersche Differenzialgleichungen

Allgemeine Form der Eulerschen Differenzialgleichung

Eine Eulersche Differenzialgleichung ist eine spezielle lineare Differenzialgleichung mit variablen Koeffizienten. Ihre allgemeine Form

kann unter Verwendung des Summensymbols auch in der Form aufgeschrieben werden.

Grundsätzlich gelten alle Aussagen, die für die linearen Differenzialgleichungen (mit beliebigen Koeffizienten vor den Ableitungen) allgemein gelten. Sie werden hier noch einmal zusammengestellt:

Dass die Koeffizienten, die vor den Ableitungen der gesuchten Funktion stehen, Ausdrücke mit genau der gleichen Potenz wie der Grad der Ableitung sind, ist kein Zufall (die Eulersche Differenzialgleichung ist durchaus keine "akademische Spezialkonstruktion" der Mathematiker, weil man für sie geschlossene Lösungen findet). Wenn (wie für Probleme der Technischen Mechanik typisch) nach dimensionsbehafteten Größen abgeleitet wird, dann ändert sich die Dimension des Ausdrucks (aus einem y-Wert mit der Dimension N/mm² wird bei Ableitung nach der mit der Dimension mm behafteten Variablen x ein y' mit der Dimension N/mm³, siehe nachfolgendes Beispiel). Da aber die Terme der Differenzialgleichung nur addiert werden können, wenn jeder Summand die gleiche Dimension hat, kann dies z. B. durch einen entsprechenden Faktor vor der Ableitung ausgeglichen werden.

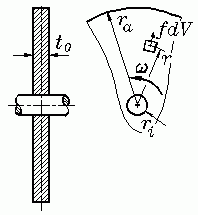
Beispiel: Für die Berechnung der Radialspannungen σ_r (Dimension z. B.: N/mm²) in einer mit der Winkelgeschwindigkeit ω rotierenden Kreisringscheibe wird im Kapitel "Rotationssysmmetrische Modelle" die Differenzialgleichung hergeleitet:

(ν ist die Querkontraktionszahl des Materials, ρ seine Dichte, die Koordinate r, die z. B. in mm gemessen wird, beginnt am Scheibenmittelpunkt). Dies ist eine Eulersche Differenzialgleichung.

Lösung der homogenen Eulerschen Differenzialgleichung

Für die homogene Eulersche Differenzialgleichung

gibt es eine zuverlässig funktionierende Strategie, n linear unabhängige Partikulärlösungen (und damit die allgemeine Lösung der homogenen Differenzialgleichung) zu finden. Mit der Substitution geht die Eulersche Differenzialgleichung in eine lineare Differenzialgleichung mit konstanten Koeffizienten über. Dass dies funktioniert, wird schon beim Umschreiben der ersten beiden Ableitungen nach x in Ableitungen nach t erkennbar (mit Strichen werden Ableitungen nach x und mit Punkten Ableitungen nach t gekennzeichnet): Die Faktoren bei den Substitutionen der Ableitungen lassen die variablen Koeffizienten verschwinden, wie man an der Substitution für eine Eulersche Differenzialgleichung 2. Ordnung sieht: Auch für die höheren Ableitungen lassen sich die Transformationsformeln herleiten: Damit ist die Strategie klar:

In der Technischen Mechanik treten Eulersche Differenzialgleichungen bis zur 4. Ordnung auf. Unter Verwendung der oben genannten Transformation und der Formeln für die Ableitungen wird aus einer Eulerschen Differenzialgleichung 4. Ordnung

die lineare Differenzialgleichung 4. Ordnung mit konstanten Koeffizienten

Eine Eulersche Differenzialgleichung 4. Ordnung wird auf der Seite "Rotationssysmmetrische Kreis- und Kreisringplatten" vorgestellt. Hier soll die Strategie an einem einfacheren Beispiel demonstriert werden.

Beispiel: Für die eingangs bereits vorgestellte Eulersche Differenzialgleichung 2. Ordnung für die Spannungsberechnung in einer rotierenden Kreisringscheibe

soll das Fundamentalsystem für die zugehörige homogene Differenzalgleichung berechnet werden (Striche kennzeichnen hier die Ableitungen nach r). Die Differenzialgleichung hat die Koeffizienten a₂ = 1, a₁ = 3 und a₀ = 0, so dass die Transformation r = e ^t auf folgende Differenzialgleichung mit konstanten Koeffizienten führt: Entsprechend der Strategie für die homogenen Differenzialgleichungen mit konstanten Koeffizienten wird mit einem Ansatz (σ_r = e ^λ t ) nach Partikulärlösungen für die homogene Differenzialgleichung gesucht. Man beachte, dass dieser Ansatz nichts mit der ähnlich aussehenden bereits durchgeführten Transformation zu tun hat. Einsetzen des Ansatzes in die Differenzialgleichung mit konstanten Koeffizienten liefert über die charakteristische Gleichung die beiden λ-Werte λ₁ = 0 und λ₂ = −2, mit denen das Fundamentalsystem und damit die Lösung für die transformierte homogene Differenzialgleichung aufgeschrieben werden kann: Die Rücksubstitution (e ^t  = r) liefert die Lösung der homogenen Eulerschen Differenzialgleichung

Patikulärlösung für die inhomogene Eulersche Differenzialgleichung

Für die Suche nach einer Partikulärlösung für die inhomogene Eulersche Differenzialgleichung

kann kein allgemeingültiges Rezept empfohlen werden. Für die Eulerschen Differenzialgleichungen, die in der Technischen Mechanik auftauchen, sind aber recht einfache Strategien bekannt, um zu einer Partikulärlösung zu kommen.

Für den wichtigsten Anwendungsfall einer Eulersche Differenzialgleichung 4. Ordnung wird auf der Seite "Rotationssysmmetrische Kreis- und Kreisringplatten" eine besonders elegante Methode vorgestellt. Hier soll eine einfache Strategie an dem bereits behandelten Beispiel demonstriert werden.

Beispiel: Für die Differenzialgleichung für die Berechnung der Radialspannungen in einer rotierenden Scheibe

wurde die Lösung der zugehörigen homogenen Differenzialgleichung mittels Transformation der unabhängigen Variablen r = e ^t bereits gefunden. Man kann nun die Transformation auf das Störglied erweitern und erhält mit der inhomogenen lineare Differenzialgleichung mit konstanten Koeffizienten die Möglichkeit, den gesamten Katalog zu nutzen, der für die Partikulärlösungssuche für diesen Differenzialgleichungstyp verfügbar ist. In der entsprechenden Tabelle wird für dieses Störglied der Ansatz empfohlen. Einsetzen in die transformierte inhomogene Differenzialgleichung liefert den Ansatzparameter: Damit ist die Partikulärlösung für die Differenzialgleichung mit konstanten Koeffizienten bekannt, die nach Rücktransformation die gesuchte Partikulärlösung der inhomogenen Eulerschen Differenzialgleichung ist: Mit der bereits oben berechneten Lösung für die homogene Eulersche Differenzialgleichung kann nun die allgemeine Lösung der Differenzialgleichung für die Spannungsberechnung in einer rotierenden Kreisringscheibe aufgeschrieben werden: Die beiden Integrationskonstanten müssen für ein spezielles Problem an zwei Randbedingungen angepasst werden, um die spzielle Lösung zu finden. Eine solche Aufgabe wird im Kapitel "Rotationssysmmetrische Modelle" gelöst.