Differenzialgleichungen 1. Ordnung

Differenzialgleichungen 1. Ordnung

In einer Differenzialgleichung 1. Ordnung darf nur die 1. Ableitung der gesuchten Funktion y(x) vorkommen. Ihre allgemeine Form lautet:

Als Lösungsstrategie bietet sich die "Trennung der Variablen" an, gegebenenfalls gekoppelt mit einer geeigneten Variablensubstitution.

Einfaches Beispiel: Seilhaftung

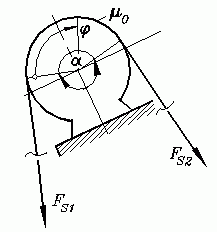
Über einen feststehenden Zylinder wird ein Seil geführt, das an den Enden durch zwei unterschiedliche Kräfte F_S1 bzw. F_S2 so belastet ist, dass es infolge der Haftung zwischen Seil und Zylinder nicht rutscht (Haftungskoeffizient: μ₀).

Für die Berechnung der Kraft F_S im Seil, die im Umschlingungsbereich kontinuierlich veränderlich ist, wird im Kapitel "Haftung" folgende Differenzialgleichung hergeleitet:

Sie wird durch "Trennung der Variablen" gelöst. Entsprechend werden alle Ausdrücke, die F_S enthalten, auf die linke Seite gebracht, alle Ausdrücke mit φ auf die rechte Seite. Danach wird auf beiden Seiten integriert: In diesem Fall sind es Grundintegrale, so dass das Ergebnis sofort aufgeschrieben werden kann: Eigentlich entsteht bei unbestimmter Integration auf beiden Seiten jeweils eine Integrationskonstante, die jedoch zu einer Konstanten C zusammengefasst werden können. Das Ergebnis wird nach F_S umgestellt: mit der neuen Konstanten C.

Damit ist die allgemeine Lösung der Differenzialgleichung bekannt. Weil eine Differenzialgleichung 1. Ordnung gelöst wurde, enthält sie eine Integrationskonstante. Diese wird bestimmt, indem die allgemeine Lösung dem aktuellen problem angepasst wird. Hier kann zum Beispiel gefordert werden, dass die Seilkraft F_S bei  φ = 0 (Beginn der Umschlingung des Zylinders) gleich der dort angreifenden äußeren Kraft F_S1 ist. Aus dieser "Anfangsbedingung"

errechnet man durch Ensetzen in die allgemeine Lösung die Integrationskonstante  C = F_S1, und damit hat man schließlich die spezielle Lösung für das aktuelle Problem: Nun kann zum Beispiel die Frage nach der Seilkraft bei  φ = α (am Ende der Umschlingung) beantworten und kennt damit den Mindestwert, den F_S2 haben muss, um ein Rutschen des Seils über den Zylinder zu verhindern.

Beispiel: Substitution und Trennung der Variablen

Einfache Beispiele für Differenzialgleichungen 1. Ordnung findet man in der Technischen Mechanik kaum. Deshalb wird aus zwei Gründen auf ein Problem aus der Optik zurückgegriffen: Die geschlossene Lösung lässt sich daran sehr schön zeigen, und es dient gleichzeitig als Einführungsbeispiel für die numerische Lösung von nichtlinearen Anfangswertproblemen, die ein besonders wichtiges Gebiet der Technischen Mechanik sind.

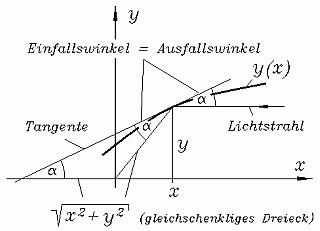
Die Aufgabe, die Funktion y(x) zu bestimmen, die einen Spiegel definiert, der paralleles Licht so ablenkt, dass sich alle Lichtstrahlen in einem Punkt (Fokus) treffen, kann ohne Einschränkung der Allgemeinheit für Lichtstrahlen parallel zur x-Achse und mit dem Nullpunkt als Fokus formuliert werden (nebenstehende Skizze). Es führt auf die nichtlineare Differenzialgleichung 1. Ordnung:

Die Lösung dieser Differenzialgleichung wird auf der Seite "Differenzialgleichungen 1. Ordnung, Beispiel: Parabolspiegel" ausführlich beschrieben.

Lösbarkeit von Differenzialgleichungen 1. Ordnung

So einfach wie im gerade demonstrierten Beispiel ist es nicht immer. Es lassen sich nicht alle Differenzialgleichungen 1. Ordnung geschlossen lösen, auch wenn man neben der Strategie der Trennung der Variablen noch andere Tricks anwendet (geeignete Substitutionen). Man bedenke, dass ja nicht einmal alle unbestimmten Integrale geschlossen lösbar sind.

Es ist also durchaus möglich, dass man selbst bei Differenzialgleichungen 1. Ordnung nur mit numerischen Verfahren zum Ziel kommt.