Strategien
Nichtlineare Differenzialgleichungen sind nur in sehr seltenen Ausnahmefällen analytisch lösbar. In der Technischen Mechanik spielen die wenigen Fälle, bei denen mit geeigneten Substitutionen und anderen Tricks geschlossene Lösungen erzeugt werden können, praktisch keine Rolle.
Aber nichtlineare Differenzialgleichungen und Differenzialgleichungssysteme treten in der Technischen Mechanik sehr häufig auf. Es sind im Wesentlichen zwei Strategien, die für die Lösung solcher Aufgaben empfohlen werden können:
- Durch Linearisierung werden nichtlineare Differenzialgleichungen zu linearen Differenzialgleichungen. Damit entfernt man sich aber immer von dem Problem, das mit der Original-Differenzialgleichung beschrieben wird. In vielen Fällen ist der Fehler, der mit der Linearisierung in Kauf genommen werden muss, abschätzbar. Der Praktiker weiß auch, dass schon beim Aufstellen der nichtlinearen Differenzialgleichung zwangsläufig so viele Idealisierungen vorgenommen werden mussten, dass sich das mathematische Modell durch eine Linearisierung gar nicht wesentlich weiter vom Originalproblem entfernt.
- Als Alternative bleibt eigentlich nur die numerische Lösung. Diese Verfahren haben zwar den Nachteil, dass in der Regel der Einfluss wichtiger Problemparameter auf das Ergebnis nicht mehr zu erkennen ist. Deshalb muss gegebenenfalls mehrfach (bei Variation der Parameter) gerechnet werden. Für die Lösung der typischen nichtlinearen Anfangswertprobleme in der Kinetik gibt es allerdings keine Alternative zu den numerischen Verfahren.
Linearisierung
Die Linearisierung einer Differenzialgleichung ist immer auch eine Verfälschung des mathematischen Modells, das die Differenzialgleichung repräsentiert. Deshalb kann man immer nur am konkreten Problem entscheiden, ob die Vereinfachung gerechtfertigt ist. Hier werden zwei typische Beispiele aus der Technischen Mechanik demonstriert.
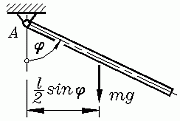
Einfaches Pendel: Die Pendelbewegung eines dünnen Stabs wird (bei Vernachlässigung von Bewegungswiderständen wie Lagerreibung und Luftwiderstand) durch das nichtlineare Anfangswertproblem (Kapitel "Kinetik starrer Körper")
beschrieben (g ist die Erdbeschleunigung, l die Stablänge). Punkte über der Variablen bedeuten: Ableitung nach der Zeit t. Das Pendel wird zur Zeit t=0 um den Winkel φ0 ausgelenkt und dann ohne Anfangsgeschwindigkeit freigelassen. Es soll die freie Schwingung (ohne Erregerkräfte oder -momente) betrachtet werden: Das Pendel wird ausgelenkt und dann sich selbst überlassen.
Es wird sich eine Schwingung mit konstanter Amplitude (jeweils gleich der Anfangsauslenkung φ0) einstellen. Die Zeit, die dabei für eine volle Schwingung ("einmal hin und zurück") benötigt wird, ist von der Anfangsauslenkung abhängig. Die Lösung ist nur numerisch möglich, man findet sie hier.
Bei Beschränkung auf "kleine" Anfangsauslenkungen φ0 bleiben die Winkel klein, und man kann die für kleine Winkel geltende Näherung
nutzen, um die Differenzialgleichung zu linearisieren. Man erhält mit
eine homogene lineare Differenzialgleichung 2. Ordnung mit konstanten Koffizienten, die in geschlossener Form lösbar ist. Eine entsprechende Differenzialgleichung ist als Eingangsbeispiel gelöst worden. Aus der Lösung kann man dann zum Beispiel die Dauer T einer vollen Schwingung als Formel ablesen:
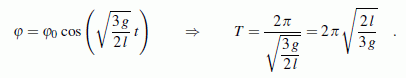
Bemerkenswert ist, dass die Schwingungsdauer T bei kleinen Pendelausschlägen von der Anfangsauslenkung unabhägig ist. Dies gilt für große Anfangsauslenkungen nicht.
Ob die Linearisierung gerechtfertigt ist, kann nicht generell entschieden werden (ist natürlich von den Genauigkeitsanforderungen abhängig). Ganz gewiss darf man aber zum Beispiel ein Pendel mit einer Auslenkung von maximal 5° mit der linearisierten Differenzialgleichung berechnen.
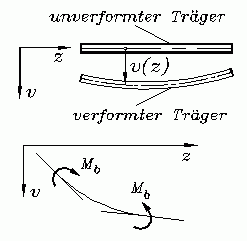
Biegelinie: Im Kapitel "Verformungen durch Biegemomente" wird gezeigt, dass das Biegemoment umgekehrt proportional zum Krümmungsradius der verformten Schwerpunktfaser ist. Auf dieser Basis erhält man für die Berechnung der Durchbiegung v(z) eines durch Biegemomente Mb belasteten geraden Trägers die nichtlineare Differenzialgleichung
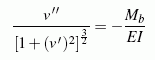
(EI ist die Biegesteifigkeit). Diese Differenzialgleichung sollte man tatsächlich nur verwenden, wenn ausgesprochen große Verformungen erfasst werden müssen (zum Beispiel die Verformung des Stabs eines Stabhochspringers).
Bei fast allen Problemen der technischen Praxis sind die Durchbiegungen sehr klein im Verhältnis zu den Abmessungen des Biegeträgers. Man denke an die Verformungen von Wellen im Maschinenbau, aber auch im Bauwesen sind die Verformungen zum Beispiel von Brückenträgern klein gegenüber seinen Abmessungen. Deshalb ist es fast immer gerechtfertigt, so zu argumentieren:
Bei sehr kleinen Verformungen v(z) ist insbesondere der Anstieg der Biegelinie v' ebenfalls sehr klein, so dass das noch viel kleinere (v')2 gegenüber 1 vernachlässigt werden kann (noch bei einem Anstieg von 5° ergibt sich mit 1+(v')2 = 1+(tan5°)2 = 1,00765 ein Fehler kleiner als 1%). Damit erhält man für kleine Verformungen mit
die Differenzialgleichung der Biegelinie 2. Ordnung, die für nahezu alle Probleme der technischen Praxis mit mehr als ausreichender Genauigkeit verwendet werden kann.

