Sukzessive Intervallhalbierung
Der Fehler bei der Anwendung der Newton-Cotes-Formeln ist schwer abzuschätzen. Es ist deshalb zu empfehlen, die Rechnung mehrfach mit unterschiedlich feiner Unterteilung des Integrationsintervalls auszuführen. Dabei ist es vorteilhaft, die Anzahl der Abschnitte n jeweils zu verdoppeln, weil dann die Punkte der vorangegangenen Rechnung wieder getroffen und die berechneten Funktionswerte wieder verwendet werden können.
Die folgende am Beispiel der Trapezregel demonstrierten Strategie ist sinnvoll: Bei Einteilung des Integrationsintervalls in n Abschnitte ergibt die Trapezregel diese Näherung:
Die Funktionswerte mit den geraden Indizes wurden bereits für die Einteilung in n/2 Abschnitte ermittelt:
Ein Vergleich dieser beiden Formeln zeigt, dass der genauere Wert In unter Verwendung des groberen Wertes nach
berechnet werden kann. Für eine fortgesetzte Intervallhalbierung ist dies eine effektive Rekursionsformel auf der Basis der zusammengesetzten Trapezregel.
Verfahren von Romberg
Wenn zwei mit unterschiedlichen Unterteilungen des Integrationsintervalls n1 und n2 ermittelte Näherungen In1 und In2 bekannt sind, kann das Ergebnis noch weiter verbessert werden (Strategie der so genannten Richardson-Extrapolation). Dies wird zunächst am Beispiel der Trapezregel demonstriert. Unter Einbeziehung der Formeln für den Fehler der Trapezregel kann der exakte Wert des Integrals I so formuliert werden:
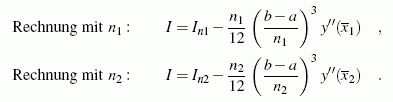
Wäre die zweite Ableitung des Integranden im Integrationsbereich konstant, so gäbe es in diesen beiden Gleichungen nur die beiden Unbekannten y'' und I, die dann aus den Gleichungen berechnet werden könnten. Unter der Voraussetzung, dass y'' nur schwach veränderlich ist, kann man
setzen und I aus den beiden Gleichungen ausrechnen. Das ist dann zwar nicht mehr der exakte Wert, aber man darf erwarten, dass es ein verbesserter Näherungswert ist:
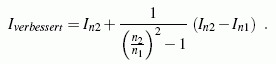
Für n2 = 2 n1 entspricht diese Formel genau der Simpsonschen Regel, wie man durch Einsetzen der entsprechenden Beziehungen leicht bestätigen kann.
Die demonstrierte Vorgehensweise kann nun auch mit der Simpsonschen Regel durchgeführt werden, und es zeigt sich derselbe Effekt: Die erzielte Verbesserung entspricht der Qualität der nächstbesseren Newton-Cotes-Formel. Allgemein gilt die Rekursionsformel nach ROMBERG:
Hierin ist für die Trapezregel ν=1, für die Simpsonsche Regel ν=2 zu setzen usw. Besonders interessant wird diese Formel jedoch durch rekursive Anwendung, wodurch sich die Benutzung von Newton-Cotes-Formeln höheren Grades erübrigt. Es genügt, die Trapezregel bei fortgesetzter Intervallhalbierung zu benutzen, und weil man mit der Romberg-Formel jeweils den bestmöglichen Wert auf der Basis der bis dahin verfügbaren Stützstellen erreicht, arbeitet dieses Verfahren für äquidistante Stützstellen optimal.
Durch den Vergleich der nach den jeweils beiden letzten Schritten erzielten Näherungen kann man entscheiden, wann eine gewünschte Genauigkeit erreicht wurde. Die Verfahren, die in Mathematikprogrammen für die numerische Integration bei vorzugebender Genauigkeit verfügbar sind, arbeiten deshalb nach diesem oder einem verwandten Verfahren.

