Die Idee
Die Lösung eines bestimmten Integrals bezieht sich immer auf einen bestimmten Bereich. In der Finite-Elemente-Theorie spielen die Ansatzfunktionen eine wichtige Rolle, die sich stets auf ein Element beziehen. In diesen und vielen anderen Fällen ist es zweckmäßig, mit speziellen lokalen (nur in dem interessierenden Bereich geltenden) Koordinaten zu arbeiten. Dabei werden diese so genannten natürlichen Koordinaten so normiert, dass sie in dem Bereich nur Werte zwischen -1 und +1 (bzw. 0 und 1) annehmen.
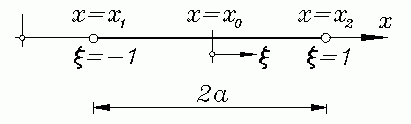
Die nebenstehende Skizze zeigt auf der x-Achse den Bereich x1 ≤ x ≤ x2. Er hat die Länge x2−x1=2a. In die Mitte dieses Bereichs bei x0=(x1+x2)/2 wird der Ursprung der natürlichen Koordinate ξ gelegt. Man bestätigt leicht, dass zwischen den Koordinaten x und ξ der Zusammenhang
besteht. Diese Formel wurde zum Beispiel genutzt, um die in natürlichen Koordinaten gegebenen Stützpunkte für die Gaußschen Quadraturformeln auf die x-Koordinaten umzurechnen.
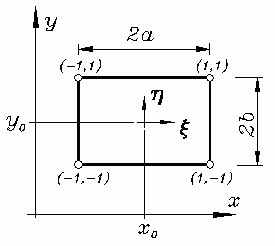
Natürliche Koordinaten für einen Rechteckbereich
Die oben angestellten Überlegungen lassen sich analog auf einen Rechteckbereich, übertragen, wenn die Rechteckseiten parallel zu den Koordinatenachsen liegen: Für ein Rechteck mit den Abmessung 2a·2b (nebenstehende Ski8zze) wird der Mittelpunkt als Ursprung des natürlichen ξ-η-Koordinatensystems gewählt. Dann kann der Zusammenhang zwischen dem x-y-Koordinatensystem und den natürlichen Koordinaten folgendermaßen formuliert werden:
besteht. Diese Formel wurde zum Beispiel genutzt, um die in natürlichen Koordinaten gegebenen Stützpunkte für die Gaußschen Quadraturformeln für Rechteckbereiche auf die x-y-Koordinaten umzurechnen.
Man beachte, dass der Rechteckbereich im x-y-Koordinatensystem durch diese Transformation in ein Quadrat im ξ-η-Koordinatensystem verwandelt wird.
Dreieckbereiche, Flächenkoordinaten
Bereiche in der x-y-Ebene, die nicht (wie der oben behandelte Rechteckbereich) durch Geraden parallel zu den Koordinaten begrenzt werden, sind schwierig zu handhaben. Oft ist man gut beraten (und in der Finite-Elemente-Praxis zum Beispiel ist dies der übliche Weg), solche Bereiche in Dreiecke zu zerlegen, weil man damit jeden beliebigen Bereich (bei geraden Rändern) erfassen oder zumindest (bei gekrümmten Rändern) annähern kann. Deshalb haben natürliche Koordinaten für einen Dreieckbereich eine besondere Bedeutung.
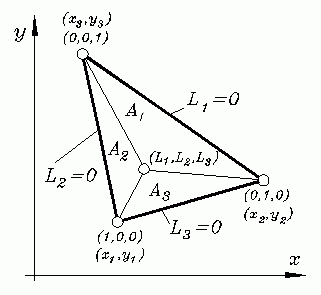
Diese Koordinaten heißen Flächenkoordinaten, die nebenstehende Skizze zeigt, wie sie definiert sind: Das betrachtete Dreieck sei im x-y-Koordinatensystem durch die sechs Koordinaten x1, y1, x2, y2, x3, y3 seiner drei Eckpunkte gegeben. Die natürlichen Koordinaten für einen Punkt im Inneren des Dreiecks werden folgendermaßen definiert: Von dem Punkt aus werden Geraden zu den drei Eckpunkten des Dreiecks gezogen, so dass drei Teildreiecke A1, A2 und A3 entstehen. Die Verhältnisse der Flächeninhalte der Teildreiecke zur Gesamtfläche A des Dreiecks sind die Flächenkoordinaten:
Natürlich muss die Lage eines Punktes auch durch die Angabe von zwei Koordinaten eindeutig beschrieben werden können. Die drei Flächenkoordinaten L1, L2 und L3 sind nicht unabhängig voneinander, weil
gelten muss. Man überzeugt sich leicht, dass die Eckpunkte des Dreiecks durch die in der Skizze angegebenen Koordinaten und die Dreiecksseiten durch die besonders einfachen Geradengleichungen L1=0, L2=0 und L3=0 beschrieben werden. Genauso leicht ist einzusehen, dass die x-y-Koordinaten des beliebigen Punktes im Inneren des Dreiecks mit den Flächenkoordinaten durch folgende einfachen linearen Zusammenhänge verknüpft sind:
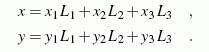
Diese Formeln wurden zum Beispiel genutzt, um die in Flächenkoordinaten gegebenen Stützpunkte für die Gaußschen Quadraturformeln für Dreiecksbereiche auf die x-y-Koordinaten umzurechnen.

