Die Idee
Der bei der Anwendung der numerischen Integrationsformeln anfallende Aufwand wird im Wesentlichen von der Anzahl der Stützstellen xi und den damit erforderlichen Berechnungen der Funktionswerte y(xi) bestimmt. Nach dem Newton-Cotes-Konzept sind diese n+1 Stützstellen äquidistant über den Integrationsbereich verteilt. Die n+1 Gewichtskoeffizienten wi, mit denen die Funktionswerte y(xi) zu multiplizieren sind, werden ermittelt, indem durch die Stützpunkte Polynome n-ter Ordnung gelegt werden, die exakt integriert werden können.
Wenn man nun durch die gleiche Anzahl von Punkten, deren Abszissen xi nicht von vornherein festgelegt werden, Polynome legt, so hat man die doppelte Anzahl von Freiwerten (n+1 Stützstellen xi und n+1 Gewichtskoeffizienten wi), die so bestimmt werden können, dass ein Polynom (2n+1)-ten Grades exakt integriert wird.
Die Herleitung dieser so genannten GAUSSschen Quadraturformeln ist recht aufwendig. Hier werden nur die für den Praktiker wichtigen Ergebnisse angegeben.
Formeln für die Gauß-Integration
Die im Folgenden angegebenen Abszissen der Integrationspunkte beziehen sich auf natürliche Koordinaten, auf die der Integrationsbereich transformiert wurde:
Dies bedeutet keine Einschränkung der Allgemeinheit, denn für ein beliebiges Intervall kann die Formel
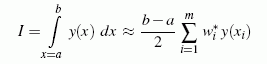
(m ist die Anzahl der Stützstellen) mit Hilfe der Transformation
benutzt werden. Die Stützstellen sind symmetrisch zu ξ = 0. Man kann sie und die zugehörigen Gewichtskoeffizienten wi* für sechs verschiedene Gauß-Formeln der nachfolgenden Tabelle entnehmen:
| m | ξi | wi* |
| 1 | 0,0000 0000 0000 | 2,0000 0000 0000 |
| 2 | ± 0,5773 5026 9190 | 1,0000 0000 0000 |
| 3 | 0,0000 0000 0000 ± 0,7745 9666 9241 |
0,8888 8888 8889 0,5555 5555 5556 |
| 4 | ± 0,3399 8104 3585 ± 0,8611 3631 1594 |
0,6521 4515 4863 0,3478 5484 5137 |
| 5 | 0,0000 0000 0000 ± 0,5384 6931 0106 ± 0,9061 7984 5939 |
0,5688 8888 8889 0,4786 2867 0499 0,2369 2688 5056 |
| 6 | ± 0,2386 1918 6083 ± 0,6612 0938 6466 ± 0,9324 6951 4203 |
0,4679 1393 4573 0,3607 6157 3048 0,1713 2449 2379 |
Anwendungsempfehlungen
Eine Gauß-Formel für m Stützstellen erfordert die Berechnung von m Funktionswerten und integriert Polynome bis zum Grad 2m-1 exakt (bei 2 Stützstellen integriert die Gauß-Formel Polynome 3. Grades exakt, vergleichbar ist die Trapezregel mit 2 Funktionswertberechnungen, die nur Funktionen 1. Grades exakt integriert). Dieses Verhältnis von Genauigkeit zu Aufwand wird von keiner anderen Integrationsformel erreicht.
Der Trick, der mit der geschickten Festlegung der Punkte im Integrationsbereich zu optimalen Ergebnissen führt, wird schon an der Formel für m = 1 deutlich: Es muss nur ein Funktionswert berechnet werden. Weil dieser aber in der Mitte des Intervalls liegt, wird die genäherte Fläche unter der horizontalen Geraden, die durch den einen Funktionswert bestimmt wird, in einer Intervallhälfte etwas zu groß, in der anderen Hälfte etwas zu klein sein, so dass die beiden Fehler sich zum Teil ausgleichen.
Bei relativ großen Integrationsbereichen ist die Verwendung einer Gauß-Formel mit großem m zu empfehlen. Die Einteilung in Teilintervalle, in denen einfachere Formeln verwendet werden, ist weniger effektiv als bei den Newton-Cotes-Formeln, weil die Mehrfach-Nutzung der Werte auf den Teilintervallgrenzen (wie bei den Newton-Cotes-Formeln) nicht möglich ist.
Auch für die sukzessive Intervallhalbierung, wie sie zur Abschätzung des Fehlers in besonderer Form durch das Romberg-Verfahren realisiert wird, sind die Gauß-Formeln wenig geeignet, weil in jedem Schritt sämtliche Funktionswerte neu berechnet werden müssten. Für die Aufgabe, ein Integral mit vorgegebener Genauigkeit zu berechnen, ist im Allgemeinen das Romberg-Verfahren zu empfehlen.
Der weitaus größte Anwendungsbereich für die Gauß-Formeln sind Finite-Elemente-Programme, wo außerordentlich viele Integrationen über relativ kleine Bereiche anfallen. Weil die Ansatzfunktionen, über die in Finite-Elemente-Programmen integriert werden muss, in der Regel Polynom-Funktionen sind, kann man bei Auswahl der passenden Gauß-Formeln häufig sogar erreichen, dass die Integrationsergebnisse exakt sind.

