Die Strategie der numerischen Integration
Die Berechnung des bestimmten Integrals
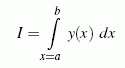
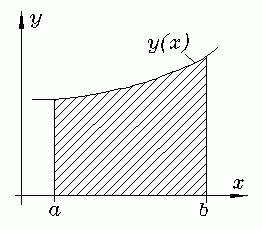
ist häufig außerordentlich aufwendig und auch nicht für jeden Integranden y(x) in geschlossener Form möglich. Weil das Ergebnis der Integration die Fläche unter der Kurve repräsentiert (nebenstehende Skizze), ist die folgende Strategie naheliegend:
Das Integrationsintervall a ≤ x ≤ b wird in n äquidistante Abschnitte der Breite
unterteilt, und für jeden (schmalen) Streifen wird näherungsweise die Fläche berechnet. Die Summe dieser Teilflächen ist dann eine Näherung für das bestimmte Integral.
Die zahlreichen Formeln, die dafür entwickelt wurden, unterscheiden sich darin, wie genau die Teilflächenermittlung durchgeführt wird. Alle Formeln haben prinzipiell den gleichen Aufbau
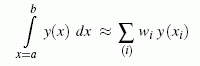
mit den Funktionswerten y(xi) an den "Stützstellen" xi und den "Gewichtskoeffizienten" wi, und für alle Formeln gilt: Je größer die Anzahl der Abschnitte n, in die das Intervall unterteilt wird, desto besser ist die Näherung.
Übersicht über die Verfahren
- Die NEWTON-COTES-Formeln entstehen, wenn durch die Punkte an den Stützstellen Interpolationspolynome gelegt werden: Durch 2 Punkte kann man eindeutig eine Gerade legen, durch 3 Punkte eine quadratische Parabel usw. Diese Polynomfunktionen ersetzen bereichsweise den Integranden y(x), können integriert werden und führen zu recht einfachen Formeln, die in der Regel den Ansprüchen genügen.
- Mit einer einfachen Newton-Cotes-Formel startend, berechnen rekursiv arbeitende Verfahren bei immer feinerer Einteilung des Integrationsbereichs den Wert des Integrals mit einer vorzugebenden Genauigkeit. Der große Vorteil dieser Verfahren liegt darin, dass der Anwender seine Genauigkeitsansprüche formulieren kann. Von der großen Anzahl der nach dieser Strategie arbeitenden Verfahren wird hier das ROMBERG-Verfahren vorgestellt.
- Als Alternative zu den Verfahren, die mit äquidistanten Stützstellen arbeiten, liefern die GAUSSschen Quadraturformeln das Ergebnis mit einem optimalen Verhältnis zwischen Aufwand (Anzahl der Funktionswertberechnungen) und Genauigkeit. Diese Formeln finden Verwendung, wenn außerordentlich viele Integrationen ausgeführt werden müssen (wie zum Beispiel bei der Element-Berechnung in Finite-Elemente-Programmen) oder wenn Mehrfachintegrale über Gebiete mit komplizierter Berandung berechnet werden sollen.

