Doppelintegrale für Rechteck- und Dreieckbereiche

Rechteckbereiche

Im einfachsten Fall eines Rechteckbereichs mit parallelen Seiten zum x-y-Koordinatensystem kann das Doppelintegral

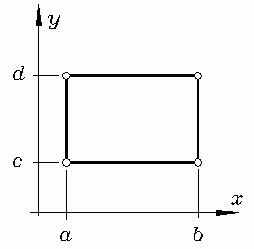
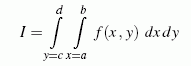
durch zweimalige Anwendung einer beliebigen Quadraturformel für den eindimensionalen Fall gelöst werden:

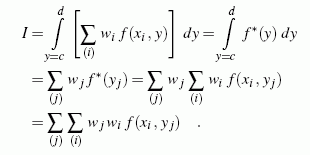
In dieser Formel kann die Anzahl der Integrationspunkte in x- bzw. y-Richtung unterschiedlich sein. Die Stützstellen und die Gewichtskoeffizienten können durch Kombination beliebiger Newton-Cotes- bzw. Gauß-Formeln gewonnen werden.

Gaußsche Quadraturformeln für Rechteckbereiche

Die Strategie entspricht exakt dem Vorgehen im eindimensionalen Fall: Das Rechteck wird mit Hilfe natürlicher Koordinaten auf ein Einheitsquadrat transformiert. Mit der doppelten Anwendung der Formel für das Integral im eindimensionalen Fall kann das Doppelintegral wie folgt aufgeschrieben werden:

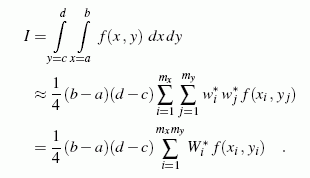
Dabei darf die Anzahl der Stützstellen in x- bzw. y-Richtung durchaus unterschiedlich sein (m_x ≠ m_y). Die Gewichtskoeffizienten W_i^* = w_i^*w_j^* berechnen sich aus den in der Tabelle für den eindimensionalen Fall angegebenen Werte. Die Stützstellen sind in dieser Tabelle in natürlichen Koordinaten angegeben und können nach den Formeln

umgerechnet werden.

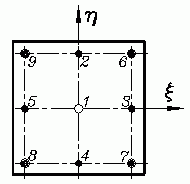
Beispiel: Für die Gauß-Quadratur mit jeweils 3 Punkten in den beiden Richtungen ergeben sich 9 Stützstellen für den Rechteckbereich. In den natürlichen Koordinaten, für die die Gauß-Punkte angegeben sind, wird der Bereich zum Quadrat, und die nebenstehende Skizze zeigt die Lage der 9 Punkte.

In der nachfolgenden Tabelle sind die Koordinaten und die Gewichtskoeffzienten für die 9 Punkte angegeben. Die Koordinaten konnten der Tabelle für den eindimensionalen Fall unmittelbar entnommen werden, die Gewichtskoeffizienten W_i^* = w_i^*w_j^* ergaben sich durch Multiplikation jeweils zweier Koeffizienten des eindimensionalen Falls.

i	ξi	ηi	Wi*
1	0,0000 0000 0000 0000	0,0000 0000 0000 0000	0,7901 2345 6790 1235
2	0,0000 0000 0000 0000	0,7745 9666 9241 4834	0,4938 2716 4938 2716
3	0,7745 9666 9241 4834	0,0000 0000 0000 0000	0,4938 2716 4938 2716
4	0,0000 0000 0000 0000	- 0,7745 9666 9241 4834	0,4938 2716 4938 2716
5	- 0,7745 9666 9241 4834	0,0000 0000 0000 0000	0,4938 2716 4938 2716
6	0,7745 9666 9241 4834	0,7745 9666 9241 4834	0,3086 4197 5308 6420
7	0,7745 9666 9241 4834	- 0,7745 9666 9241 4834	0,3086 4197 5308 6420
8	- 0,7745 9666 9241 4834	- 0,7745 9666 9241 4834	0,3086 4197 5308 6420
9	- 0,7745 9666 9241 4834	0,7745 9666 9241 4834	0,3086 4197 5308 6420

Die Zahlenwerte in der Tabelle sehen komplizierter aus als sie sind: Für die natürlichen Koordinaten gibt es neben dem Wert 0 nur die beiden Werte ±0,7745 9666 9241 4834, und die drei verschiedenen Werte der Gewichtskoeffizienten lassen sich als relativ einfache gemeine Brüche aufschreiben:

Gaußsche Quadraturformeln für Dreieckbereiche

Bereiche in der x-y-Ebene, die nicht (wie der oben behandelte Rechteckbereich) durch Geraden parallel zu den Koordinaten begrenzt werden, sind schwierig zu handhaben. Das gilt natürlich auch für die Integration über diese Bereiche. Oft ist man gut beraten (und in der Finite-Elemente-Praxis zum Beispiel ist dies der übliche Weg), solche Bereiche in Dreiecke zu zerlegen, weil man damit jeden beliebigen Bereich (bei geraden Rändern) erfassen oder zumindest (bei gekrümmten Rändern) annähern kann. Deshalb haben natürliche Koordinaten für einen Dreieckbereich (Flächenkoordinaten) eine besondere Bedeutung.

Im Gegensatz zum Rechteckbereich bieten die Newton-Cotes-Formeln keine brauchbare Basis für den Dreieckbereich, und eigentlich kann nur die Anwendung von Gaußschen Quadraturformeln empfohlen werden. Aber auch dafür kann man nicht einfach die Formeln für den eindimensionalen Bereich auf die zweite Dimension erweitern. Es muss vielmehr die Idee von Gauß, nach den Koordinaten für die Stützstellen zu suchen, die das beste Ergebnis versprechen, für das Dreieck realisiert werden.

Dies ist aufwendig, und deshalb werden hier nur die Ergebnisse für zwei Gauß-Formeln für Dreieckbereiche angegeben. Wie bei allen Gauß-Formeln wird mit natürlichen Koordinaten gearbeitet (hier: Flächenkoordinaten). Die Näherungsformel hat den typischen Aufbau:

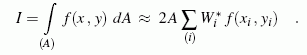
Darin ist

die doppelte Dreiecksfläche. Die Funktionswerte müssen an den Stützstellen (x_i ,y_i) berechnet werden, die aus den Flächenkoordinaten nach den bekannten Transformationsformeln berechnet werden:

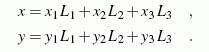
In diesen Formeln sind (x₁,y₁), (x₂,y₂), (x₃,y₃) die Koordinaten der Eckpunkte des Dreiecks.

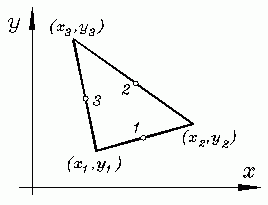
Die einfachste Gauß-Formel für das Dreieck bezieht sich auf nur 3 Stützstellen, die auf den Seitenmitten liegen. Die folgende Tabelle zeigt die Flächenkoordinaten dieser 3 Punkte mit den zugehörigen Gewichtskoeffizienten:

i	L1	L2	L3	2Wi*
1	0,5	0,5	0	0,3333 3333
2	0	0,5	0,5	0,3333 3333
3	0,5	0	0,5	0,3333 3333

Die Benutzung dieser Formeln wird hier an einem Beispiel demonstriert.

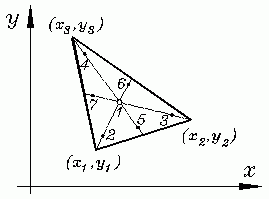
Eine wesentlich bessere Näherung erreicht man mit der nächstbesseren Gaußformel mit 7 Stützstellen. Diese liegen im Schwerpunkt des Dreiecks und auf den Seitenhalbierenden. Die Skizze zeigt die Lage der Punkte, die nachfolgende Tabelle enthält ihre Koordinaten und die zugehörigen Gewichtskoeffizienten:

i	L1	L2	L3	2Wi*
1	0,3333 3333	0,3333 3333	0,3333 3333	0,2250 0000
2	0,7974 2699	0,1012 8651	0,1012 8651	0,1259 3918
3	0,1012 8651	0,7974 2699	0,1012 8651	0,1259 3918
4	0,1012 8651	0,1012 8651	0,7974 2699	0,1259 3918
5	0,4701 4206	0,4701 4206	0,0596 1587	0,1323 9415
6	0,0596 1587	0,4701 4206	0,4701 4206	0,1323 9415
7	0,4701 4206	0,0596 1587	0,4701 4206	0,1323 9415