Kleine Testrechnung für verschiedene Verfahren mit Matlab
Das nachfolgend gelistete Matlab-Script zeigt die Ergebnisse für eine Testrechnung mit unterschiedlichen Verfahren der numerischen Integration. Außerdem wird die in Matlab für die numerische Integration verfügbare Funktion quad demonstriert. Als (beliebig austauschbarer) Integrand wurde die sin-Funktion eingetragen, die in den (ebenfalls beliebig modifizierbaren) Grenzen von 0 ... π/2 (Fläche unter einem Viertel der vollen sin-Schwingung) entsprechend
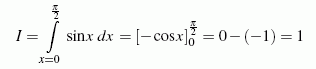
das exakte Ergebnis 1 liefern würde, mit dem die numerisch gewonnenen Werte verglichen werden können. Hier wird das Integrationsintervall für die Trapezregel und die Simpsonsche Regel in n=100 Abschnitte unterteilt, was natürlich auch beliebig geändert werden kann. Um ein anderes Integral mit anderen Grenzen und geänderter Genauigkeit zu lösen, müssen nur die weiß geschriebenen Anweisungen geändert werden. Rechts sieht man das Command Window von Matlab mit den Ergebnissen. Das Matlab-Script steht als NumInt.m zum Download zur Verfügung.
format long ;
F = inline('sin(x)'); % Integrand
a = 0 ;
b = pi/2 ; % Integrationsgrenzen
n = 100 ; % Anzahl der Abschnitte
h = (b-a) / n ; % Breite eines Abschnitts
nS = n + 1 ; % Anzahl der Stützstellen
xS = a : h : b ; % Koordinaten der Stuetzpunkte
yS = F(xS) ; % ... und Funktionswerte
% Trapezregel:
Trapez = ((yS(1)+yS(nS))/2 + sum (yS(2:n)))*h
% Simpsonsche Regel:
I = (yS(1)+yS(nS)) ; % Erster und letzer Wert der Formel
faktor = 4 ;
for i = 2:n
I = I + yS(i)*faktor ;
if (faktor == 4) faktor = 2 ;
else faktor = 4 ;
end ;
end
Simpson = I*h/3
% Einfachste Gaußformel:
xS = a+h/2 : h : b-h/2 ; % Koordinaten der Stuetzpunkte
yS = F(xS) ; % ... und Funktionswerte
Gauss = sum (yS(1:n))*h
% Die MATLAB-quad-Funktion approximiert das Integral mit
% rekursiver Anwendung der Simpsonschen Regel bis zum Erreichen
% einer vorgegebenen Genauigkeit (Voreinstellung: 1.e-6):
MatLabquad = quad (F , a , b)
MatLabquadGenauer = quad (F , a , b , 1.e-10)

Berechnung der Bogenlänge einer Bahnkurve
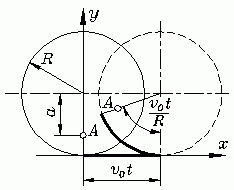
Im Kapitel "Allgemeine Bewegung des Punktes" wird die Bewegung eines Punktes A auf einem rollenden Rad verfolgt (zum Zeitpunkt t=0 befinden sich der Mittelpunkt des Rades bei x=0 und A senkrecht unter dem Mittelpunkt). Es wird gezeigt, dass sich die Bahngeschwindigkeit des Punktes A nach
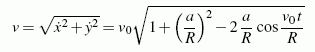
berechnen lässt.
Zur Berechnung des Weges, den der Punkt zwischen zwei Zeitpunkten t1 und t2 zurücklegt, muss die Geschwindigkeit entsprechend
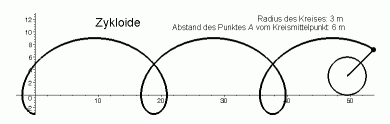
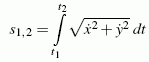
über die Zeit integriert werden. Hier soll der Weg berechnet werden, den der Punkt A bei einer vollen Umdrehung des zurücklegt. Dabei wird ein Abmessungsverhältnis von a/R=2 angenommen (A liegt außerhalb des Rades und bewegt sich auf einer so genannten "verlängerten Zykloide", das Bild zeigt eine Momentaufnahme der Animation der Bewegung).
Weil der zurückgelegte Weg für eine volle Radumdrehung natürlich weder von der Geschwindigkeit des Rades v0 noch von der Zeit abhängig ist, die dafür erforderlich ist, wird die neue Variable
eingeführt. Der Radius R wurde in die Beziehung mit hineingenommen, weil φ auf diese Weise als Winkel interpretiert werden kann, um den sich das Rad gedreht hat. Es ist also das bestimmte Integral
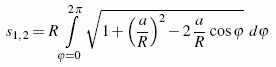
zu lösen. Das folgende Matlab-Script (Download hier) realisiert das:
clear all
a = 0 ; b = pi*2 ; % Integrationsgrenzen
disp(['Bogenlaenge: s = ', num2str(quad (@integr , a , b , 1.e-10))]) ;
function y = integr(phi)
adR = 2 ;
y = sqrt(1+adR^2-2*adR*cos(phi)) ;
Im Gegensatz zum Einführungsbeispiel, bei dem der Integrand als inline-Function definiert wurde, ist es bei etwa komplizierteren Ausdrücken ratsam, eine spezielle Function dafür zu schreiben (hier: integr), die dann der Matlab-Function quad mit vorangestelltem @-Zeichen bekanntgemacht werden muss.
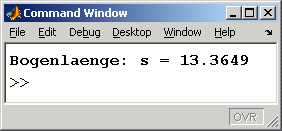
Das Command Window von Matlab zeigt das Ergebnis. Weil für den Aufruf von quad eine Genauigkeitsforderung angegeben wurde, darf das Ergebnis mit den ausgegebenen Stellen als exakt angesehen werden.
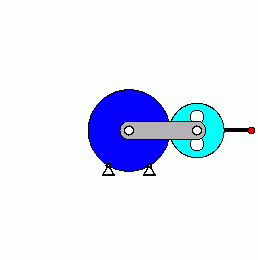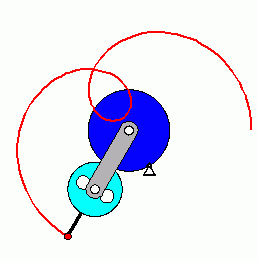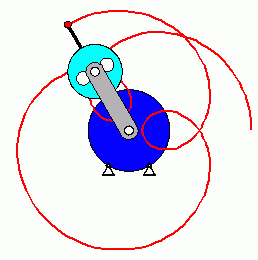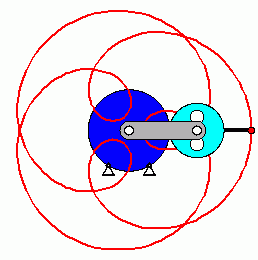
Das oben zu sehende Matlab-Script ist für andere Aufgaben leicht modifizierbar. Die Berechnung der Länge der Bahnkurve eines speziellen Punktes eines Planetengetriebes (nebenstehende Animation) findet man hier. Dort wird gezeigt, dass die Lösung des bestimmten Integrals
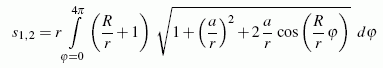
die Länge der Bahnkurve liefert. Das für dieses Integral modifizierte Matlab-Script findet man ebenfalls dort.
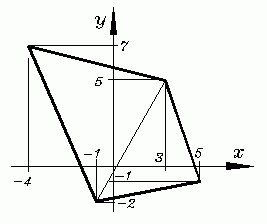
Gaußsche Quadratur für Dreieckbereiche
Für das nebenstehend zu sehende unregelmäßige Viereck soll das Deviationsmoment (vgl. Kapitel "Biegung")
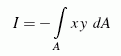
bezüglich des skizzierten Koordinatensystems berechnet werden.
Das Viereck wird in zwei Dreiecke unterteilt, für die das Integral numerisch nach den Gaußschen Quadraturformeln für Dreieckbereiche gelöst wird. Das nachfolgende Matlab-Script (steht als NumIntGauss2D_3.m zum Download zur Verfügung) realisiert dies:
format long ;
F = inline('-x*y'); % Integrand
n = 2 ; % Anzahl der Dreiecke
% x1 y1 x2 y2 x3 y3
xyEck = [ -1 , -2 , 5 , -1 , 3 , 5 ;
-1 , -2 , 3 , 5 , -5 , 7 ] ; % Eckpunkte der Dreiecke
nGauss = 3 ;
Li = [ 0.5 , 0.5 , 0 ; % Natürliche Koordinaten der Gaußpunkte
0 , 0.5 , 0.5 ;
0.5 , 0 , 0.5 ] ;
Wi2 = [ 1/3 , 1/3 , 1/3 ] ; % Gewichtskoeffizienten 2Wi*
I = 0 ;
for i = 1:n
A2 = (xyEck(i,3)-xyEck(i,1))*(xyEck(i,6)-xyEck(i,2)) - ...
(xyEck(i,5)-xyEck(i,1))*(xyEck(i,4)-xyEck(i,2)) ;
Ii = 0 ;
for j = 1:nGauss
x = xyEck(i,1)*Li(j,1) + xyEck(i,3)*Li(j,2) + xyEck(i,5)*Li(j,3) ;
y = xyEck(i,2)*Li(j,1) + xyEck(i,4)*Li(j,2) + xyEck(i,6)*Li(j,3) ;
Ii = Ii + Wi2(j)*F(x,y)*0.5 ;
end
I = I + Ii*A2 ;
end
disp(['Gauß-Formel mit 3 Punkten: I = ', num2str(I)]) ;
Im Script sind die Passagen weiß gekennzeichnet, die für die Lösung eines anderen Problems geändert werden müssten: Integrand, Anzahl der Dreiecke und die Koordinaten der Eckpunkte der Dreiecke.
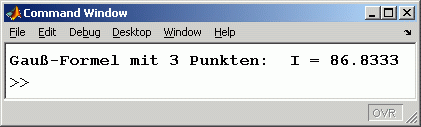
Der hellblau gekennzeichnete Bereich zeigt die Parameter der verwendeten Gauß-Formel. Es ist die einfachste Formel mit nur drei Stützpunkten. Rechts sieht man das Ergebnis der Berechnung. Man erhält den exakten Wert für das Integral. Für den recht einfachen Integranden genügt die einfachste Gauß-Formel.
Für kompliziertere Probleme kann man gegebenenfalls die hellblau dargestellten Passagen des Matlab-Scripts durch die Gauß-Formel für sieben Stützstellen ersetzen. Der gesamte übrige Teil des Scripts bleibt dabei ungeändert.

