|
Die Matlab-Functions eig und eigs Für die Berechnung der Eigenwerte und der zugehörigen Eigenfunktionen des Speziellen Matrizeneigenwertproblems
bzw. des Allgemeinen Matrizeneigenwertproblems
bietet Matlab die Functions eig und eigs an. Der Benutzer braucht sich bei der Verwendung dieser Functions um die Auswahl eines geeigneten Verfahrens nicht zu kümmern (ähnlich wie bei der Lösung linearer Gleichungssysteme mit dem Backslash-Operator). Weil aber die Lösung von Matrizeneigenwertproblemen numerisch problematischer ist als z. B. die Lösung linearer Gleichungssysteme, ist ein Mindestverständnis für die Problematik und auf jeden Fall die kritische Beurteilung der abgelieferten Lösungen dringend anzuraten. Die zu lösende Aufgabe und das Speicherformat der Matrizen entscheiden darüber, ob eig oder eigs verwendet werden sollte:
|
|
Ein Beispiel
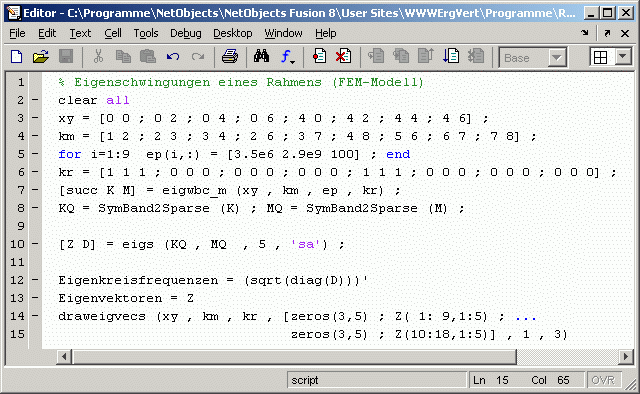
Gegeben: EI = 3,5·106 Nm2 ; EA = 2,9·109 N ; ρA = 100 kg/m ; a = 2 m . Das Finite-Elemente-Berechnungsmodell führt auf ein Allgemeines Matrizeneigenwertproblem
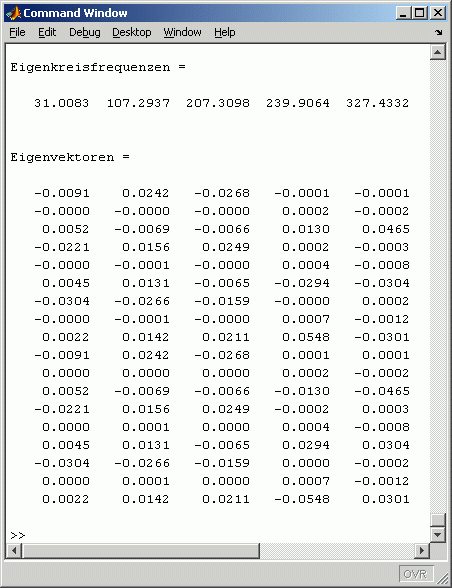
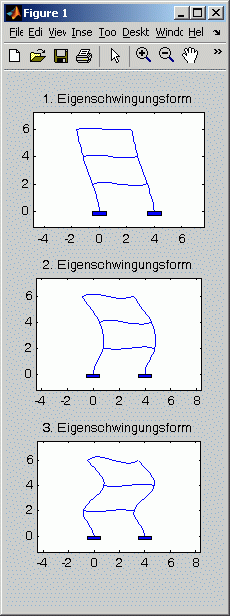
mit symmetrischen dünn besetzten Matrizen K und M. Das nachfolgend zu sehende Matlab-Script baut diese beiden Matrizen in den Zeilen 3 bis 7 mit dem Finite-Elemente-Baukasten Femset auf (für Interessenten: MatlabFemset). In Zeile 8 werden sie in das von Matlab unterstützte "Sparse matrix"-Format konvertiert (es sind Matrizen mit 18 Zeilen bzw. Spalten). Das Matrizeneigenwertproblem wird mit der Function eigs in Zeile 10 gelöst. Der Parameter auf Position 3 gibt die Anzahl der gewünschten Eigenwerte an, der Parameter 'sa' auf der Position 4 bestimmt, dass es die kleinsten Eigenwerte sein sollen (Angaben sind erforderlich, weil standardmäßig die 6 größten Eigenwerte berechnet werden). Die Eigenvektoren werden spaltenweise in einer Matrix Z abgeliefert, die Eigenwerte als Diagonalelemente in einer Diagonalmatrix. Die Eigenkreisfrequenzen und die zugehörigen Eigenvektoren werden in das Command Window ausgegeben, die ersten drei Eigenvektoren zusätzlich als Eigenschwingungsformen in einem Graphik-Fenster gezeichnet:
|
| Animation der ersten drei Eigenschwingungsformen eines biege- und dehnsteifen Rahmens |
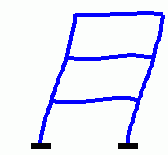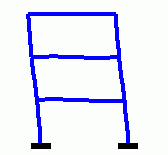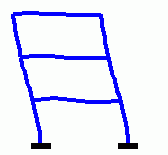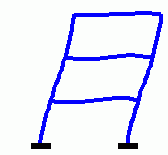
|

|
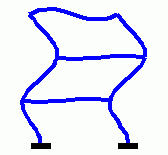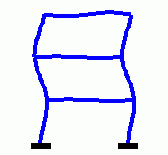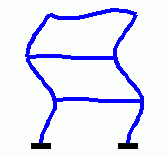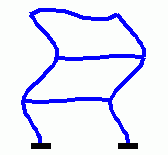
|
|
Zum Download verfügbar sind
|

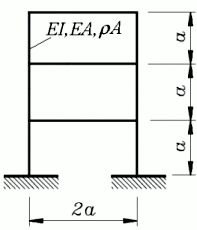 Für den skizzierten biege- und dehnsteifen Rahmen mit konstanten Querschnitten in allen Bereichen sollen die 5 kleinsten Eigenkreisfrequenzen und die zugehörigen Schwingungsformen ermittelt werden.
Für den skizzierten biege- und dehnsteifen Rahmen mit konstanten Querschnitten in allen Bereichen sollen die 5 kleinsten Eigenkreisfrequenzen und die zugehörigen Schwingungsformen ermittelt werden.